Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 63

Впервые строгое определение понятия "устойчивость" было дано русским ученым А. М. Ляпуновым в 1892 г в работе "Общая задача об устойчивости движения". Определение А. М. Ляпуновым понятия "устойчивость" наилучшим образом удовлетворяет многим техническим задачам, поэтому оно в настоящее время принято как основное.

6.2. Теоремы А. М. Ляпуноваоб устойчивости динамическихсистем

 САУ соответствует определенная система дифференциальных уравнений, которая может быть приведена в пространстве состояний к виду

где:

 y_k - обобщенные координаты системы (переменные состояния);

Y_k - известные функции, определенные в некоторой фиксированной области G пространства переменных состояния y₁, y₂, ..., y_n.

Пусть величины y₁₀, y₂₀, ..., y_n0обозначают начальные значения переменных y₁, y₂, ..., y_n. Каждой системе начальных значений y₁₀, y₂₀, ..., y_n0 соответствует решение

уравнения (4.2).

Установившиеся процессы можно описать так называемыми очевидными решениями уравнения (6.1). Эти решения

представляют собой корни уравнений

Они входят в семейство решений (6.2) и определяются начальными значениями

Обычно рассматривают случаи, когда имеется одно решение (6.3), соответствующее вполне определенному установившемуся процессу в системе управления.

Введем отклонение координат x_k от установившихся значений :

Подставляя (6.4) в уравнение (6.1), получим

где

Уравнения (6.5) называют уравнениями возмущенного движения.

Формула (6.4) определяет преобразование переноса начала координат в точку , вследствие чего (6.3) соответствует решение

По терминологии А. М. Ляпунова, уравнения (6.6) называют невозмущенным движением системы.

При t = t₀ переменные x_k принимают свои начальные значения, которые называют возмущениями. Каждой заданной системе таких возмущений отвечает однозначное и непрерывное решение

x_k = X_k(x₁₀, x₂₀, ..., x_n0, t)

уравнений (6.5). Это решение называют возмущенным движением системы.

Исследования Ляпунова об устойчивости движения позволяют судить об интересующих нас свойствах возмущенного движения, не прибегая к интегрированию уравнений (6.5), и рационально рассчитывать регулятор.

Если окажется, что при определенной настройке регулятора решение (6.6) будет устойчивым, то система управления сама, без постороннего вмешательства, изберет режим невозмущенного движения, который соответствует этому решению. Если же решение (6.6) будет неустойчивым, то такого установившегося режима получить нельзя. При сколь угодно малых возмущениях x_k0 система будет удаляться от этого режима.

В большинстве задач теории автоматического управления функции X_k(x₁, x₂,..., x_n) допускают разложение в степенные ряды, сходящиеся в некоторой        H-окрестности начала координат (6.6):

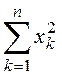< H,

если H > 0 достаточно мала. В этих случаях уравнениям (6.5) можно придать вид

где a_ks  (r, s = 1, 2, ..., n) - постоянные линейные части разложения. При этом функции F_r не содержат членов ниже 2-го порядка малости. На практике судят об устойчивости решения (6.6), рассматривая лишь уравнения, называемые уравнениями 1-го приближения вместо уравнения (6.7):

Так как справедливость замены (6.7) уравнениями (6.8) заранее не ясна, возникла задача найти случаи исследования уравнений (6.7), в которых устойчивость (неустойчивость) решения (6.6) вытекает из рассмотрения уравнений 1-го приближения (4.8). Эту задачу решил А. М. Ляпунов. Он показал, что все случаи исследования уравнений (6.8) следует разделять на категории некритических и критических случаев. К первой из них относятся случаи, в которых вопрос об устойчивости (неустойчивости) невозмущенного движения однозначно разрешается на основании исследования уравнений 1-го приближения (6.8). Для того чтобы обнаружить эти случаи, следует составить характеристическое уравнение системы