Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 53

Случайный процесс называется гауссовым, или нормальным, если все конечномерные распределения вероятностей этого процесса имеют гауссовский (нормальный) закон.

Математическое ожидание (среднее значение) случайного процесса х определяется соотношением

Математическое ожидание есть не то иное, как обыкновенная функция времени. Аналогично определяются моменты высших порядков.

Ковариация процесса задается формулой

Гауссовский случайный процесс полностью характеризуется своими математическим ожиданием и ковариацией.

Аналогично определяется взаимная ковариация для двух стохастических процессов:

Стохастический процесс называется стационарным, если конечномерное распределение вероятностей x(t₁), x(t₂), ..., x(t_n) тождественно распределению x(t₁+r), x(t₂+r), ..., x(t_n+r) для любых r, n, t₁, ..., t_n. Процесс называют слабо стационарным, если первые два момента распределений одинаковы для всехr.

Математическое ожидание (слабо) стационарного процесса постоянно. Взаимная ковариация слабо стационарных процессов зависит только от разности аргументов s - t. Несколько отступив от принятого обозначения функции, запишем

Взаимная ковариация (слабо) стационарных процессов есть функция только одного аргумента. Следовательно,

Если х- скаляр, то функция

называется автоковариацией.

Взаимная спектральная плотность (слабо) стационарных процессов - это преобразование Фурье их ковариации. Отсюда

и

Отметим, что j_xx и j_ху также принято называть автоспектральной плотностью и взаимной спектральной плотностью соответственно. Автоспектральную плотность для удобства называют просто спектральной плотностью.

Интерпретация ковариации и спектра. Стационарные гауссовские процессы полностью характеризуются своими математическим ожиданием и ковариацией. На практике всегда полезно интуитивно понимать, как свойства стохастического процесса отражаются этими функциями.

Математическое ожидание (среднее значение) почти не нуждается в разъяснениях. Значение ковариации r_o(0) в нуле есть не что иное, как дисперсия процесса, характеризующая величину его флюктуации. Если среднеквадратическое отклонение равно квадратному корню из r_x(0), то получим корреляционную функцию, определяемую как

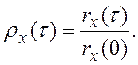
В теории стохастических процессов показано что, корреляционная функция по величине всегда меньше единицы.

Функция r_х(t) определяет взаимную зависимость значений процесса, разделенных промежутком времени t. Если она близка к единице, то это означает сильную связь, если она равна нулю - отсутствие связи, а если отрицательная, то связь отрицательная. Таким образом, исследование формы корреляционной функции позволяет судить о временной взаимозависимости процесса.

Для оценки связей стохастических процессов полезно анализировать их реализации и ковариации.

Функция спектральной плотности также имеет физическую интерпретацию. Интеграл

дает мощность сигнала в полосе частот (w₁, w₂). Таким образом, площадь, ограниченная графиком спектральной плотности, есть не что иное, как мощность сигнала в заданной полосе. Присутствие в спектре выраженных максимумов отражает наличие почти периодических компонентов. Общая площадь пропорциональна полной дисперсии сигнала. Для практической деятельности полезно знать, как свойства сигнала связаны с его спектром.

Заметим, что математическое ожидание, ковариация и спектральная плотность определяются только первыми двумя моментами стохастического процесса. Сигналы с сильно различающимися реализациями могут иметь одинаковые моменты. Так, например спектры случайной телеграфной волны, переключающейся между 0 и 1, и шума обычной RC-цепочки одинаковы.