Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 54

Дискретный "белый шум".Рассмотрим стационарный дискретный стохастический процесс , такой, что его реализации  и независимы, если t ¹ s. Тогда его можно представить как последовательность {,t = ..., -1, 0, 1, ...} независимых, одинаково распределенных случайных величин. В этом случае ковариация определяется из соотношения

.

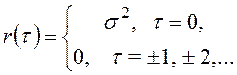Процесс с такой ковариацией называется дискретным "белым шумом". Из (4.7) следует, что его спектральная плотность равна j (w) = s²/(2p), т. е. она постоянна на всех частотах.

"Белый шум" играет важную роль в стохастической теории управления, так как любой случайный процесс можно получить на выходе динамической системы, входной сигнал которой является "белым шумом". Поэтому "белый шум" здесь играет ту же роль, что и прямоугольные импульсы в детерминированных системах.

Формирующие фильтры. Пусть {, k = ... , -1, 0, 1, ...} - дискретный "белый шум". Линейная система (формирующий фильтр), на вход которой подается "белый шум", генерирует широкий класс процессов.

В частности, стохастический процесс

называется скользящим средним, или СС-процессом.

Стохастический процесс , вырабатываемый линейной системой

называется авторегресионным, или АР-процессом.

Стохастический процесс , вырабатываемый системой

называется авторегрессионным процессом со скользящим средним, илиАРСС-процессом.

4.2. Модели стохастическихсистемв пространстве сотояний

Для стохастических систем невозможно точно определить их будующее состояние. Поэтому естественным развитием понятия состояния для этих систем является требование, чтобы распределение вероятностей следующего состояния однозначно определялось текущим. Стохастические процессы, обладающие таким свойством, получили название марковских. Таким образом, марковские процессы есть не что иное, как стохастический эквивалент моделей систем в пространстве состояний. Формально они определяются так.

Определение марковского процесса. Пусть t₁и t - такие элементы индексного множества Т, что t₁ < t₂ < ... < t_n < t. Стохастический процесс {x(t), t Î T} называется марковским, если

P {x(t) £x½ x(t₁), ..., x(t_n)} = P {x(t) £x½ x(t_n)}.

Здесь P {·½ x(t₁), ..., x(t_n)} обозначает условную вероятность при заданных x(t₁), … , x(t_n).

Марковский процесс вполне определяется распределениями начальных вероятностей F (x; t_o) = P {x(t₀) £x } и вероятностей перехода

F (x_t, t½x₂, s) = P {x(t) £x_t½ x(s) = x_s}.

Используя правило умножения условных вероятностей, можно определить все конечномерные распределения.

Линейные стохастические разностные уравнения. Рассмотрим дискретную систему, в которой период квантования равен единице.

Пусть x(k) - состояние в момент времени k. тогда распределение вероятности состояния в момент времени k + 1 есть функция x(k). Если математическое ожидание линейно по x(k) и распределение вокруг него не зависит от x(k), то x(k + 1) можно представить следующим образом:

где- случайная переменная с нулевым математическим ожиданием, не зависящая отx(k) и всех прошлых значенийх. Это означает, что также не зависит от всех прошлых . Последовательность {, k = ..., -1, 0, 1, ...} состоит из независимых, одинаково распределенных случайных переменных. Стохастический процесс {}, таким образом, представляет собой дискретный "белый шум".

Уравнение (4.10) называется линейным стохастическим разностным уравнением. Чтобы окончательно определить случайный процесс {x(k)}, необходимо задать начальные условия. Предполагается, что начальное состояние имеет математическое ожидание  и матрицу ковариации . (Ковариация случайной переменной v обозначается R_v.)

4.3 Прохождениеслучайного сигналачерез линейнуюдинамическую систему