Учебно-методический комплекс по дисциплине «Теоретические основы автоматизированного управления», страница 55

Если на вход объекта подать случайный сигнал, то его выходной сигнал также будет случайным процессом. В состав систем автоматического уравнения такими объектами, как правило, входит микропроцессорное управляющее устройство (контроллер). Динамику объекта уравнения и других элементов САУ в таких случаях описывают разностными уравнениями. Однако эти разностные уравнения будут теперь стохастическими, поэтому для их анализа следует применять специальный математический аппарат.

Исследуем характер случайного выходного сигнала системы, математическая модель которой задана в виде линейного стохастического разностного уравнения (4.10), и вычислим его первый и второй моменты.

Для получения математического ожидания

определим математические ожидания обеих частей уравнения (4.10). Так как математическое ожидание случайного процесса  равно нулю, то справедливо следующее равенство:

с начальным условием

Следовательно, математическое ожидание вычисляется так же, как и в системе без возмущений.

Чтобы вычислить ковариацию, введем функцию

где

Из уравнений (4.10) и (4.11) следует, что  удовлетворяет уравнению (4.10) с начальным условием, имеющим нулевое математическое ожидание. Для вычисления ковариации составим выражение

Определим математические ожидания его правой и левой частей и учтем, что v(k) и  независимы. В результате получим

c начальным условием

Рекурсивное уравнение дляопределяет процедуру вычисления матрицы ковариации. Чтобы вычислить ковариацию состояния

,

отметим, что

Так как v(k) и независимы и математическое ожидание v(k) равно нулю, то

Повторяя эти рассуждения, имеем

.

Полученные результаты используются при анализе и синтезе стохастических САУ, поэтому они настолько важны, что их следует систематизировать.

Теорема 4.1. Рассмотрим случайный процесс, заданный линейным стохастическим разностным уравнением (4.10) (здесь "белый шум" с нулевым математическим ожиданием и ковариацией ). Пусть начальное состояние процесса имеет математическое ожидание и ковариацию. Тогда математическое ожидание и ковариация процесса определяются соответственно как

,    t³ 0;

где задается уравнением

;

.

Замечание 1. При анализе стохастических САУ в вектор  включают переменные состояния объекта управления и других элементов САУ, а также переменные состояния формирующих фильтров стохастических возмущающих воздействий.

Замечание 2. Если распределение вероятностей стохастических входных сигналов, образующих вектор , является гауссовским, то стохастический процесс  однозначно определяется своими математическим ожиданием  и ковариацией .

Замечание 3. Если вектор управляемых переменных  стохастической САУ связан с вектором  линейным выражением

,

где  - матрица известных коэффициентов передачи, то его математическое ожидание задается уравнением

,

а ковариация – уравнением

.

Взаимная ковариацияy и х есть

.

Замечание 4. Различные члены в уравнении (4.14) имеют определенную физическую интерпретацию. Матрица  характеризует неопределенность состояния, произведение  показывает, как передается неопределенность в момент времени k в соответствии с динамикой системы, а член описывает увеличение неопределенности вследствие наличия возмущения .

4.4. Примеры и задачи

Пример 4.1.Рассмотрим систему первого порядка:

x(k + 1) = a x(k) + v(k),

где v- последовательность некоррелированных случайных величин с нулевым математическим ожиданием и ковариацией r₁. Пусть состояние в момент времени k₀ имеет математическое ожидание m₀и ковариацию r₀. Из (6.18) следует, что математическое ожидание m(k) = Ex (k) определяется соотношением m(k + 1) = a m(k), m(k₀) = m₀, откуда m(k) = a^k-k₀ m₀. Из уравнения (6.20) следует, что

P(k + 1) = a² P(k) + r₁.     P(k_o) = r_o.

Откуда получим

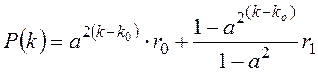
r_x(l, k) = a^l-k p(k),  l ³ k,

 r_x(l, k) = a^k-l p(l) , l < k.

Если ½а½< 1 и k_о® -¥, то