Анализ и синтез замкнутой системы автоматического управления

Реферат

99 с., 84 рис., 78 табл., прил.: 3 листа А1.

Ключевые слова: ПЕРЕДАТОЧНАЯ ФУНКЦИЯ, КАНАЛ УПРАВЛЕНИЯ (РЕГУЛИРОВАНИЯ), КАНАЛ ВОЗМУЩЕНИЯ, РЕГУЛЯТОР, ПЕРЕХОДНАЯ ХАРАКТЕРИСТИКА, АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА (АЧХ), ФАЗО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА (ФЧХ), АМПЛИТУДО-ФАЗОВАЯ ХАРАКТЕРИСТИКА (АФХ), РАСШИРЕННЫЕ ХАРАКТЕРИСТИКИ, УСТОЙЧИВОСТЬ, НАСТРОЕЧНЫЕ ПАРАМЕТРЫ, КОРНИ, ПОЛЮСА, СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (САУ), КОЛЕБАТЕЛЬНОСТЬ, ВЕЩЕСТВЕННАЯ ЧАСТОТНАЯ ХАРАКТЕРИСТИКА.

Объектом исследования является анализ и синтез замкнутой системы автоматического управления.

Цель работы – освоение методов анализа и синтеза систем автоматического управления (САУ), приобретение практических навыков расчета различных систем.

Методы исследования: использование свойств преобразований Лапласа и Фурье, и обратные их преобразования. А также в ходе работы был использован персональный  компьютер и следующее программное обеспечение: Microsoft Word, Microsoft Excel, MathCAD v14, MathType, Калькулятор.

В результате мы получили оптимальные настройки регулятора системы и доказали устойчивость системы при данных настройках.

 Данный метод синтеза замкнутой системы автоматического регулирования находит место в химической промышленности и в тех областях промышленности, где имеются значительные запаздывания в объектах управления и возмущения.

Введение

В этом курсовом проекте перед нами была поставлена следующая задача: при известных свойствах объекта (количество каналов, передаточные функции каналов и их параметры), нужно синтезировать одноконтурную замкнутую систему автоматического управления, рассчитать ее параметры при заданном регуляторе и степени колебательности. При этом нужно проанализировать полученные результаты.

Данный курсовой проект необходим для овладения базовыми навыками расчета и синтеза ЗСАУ, которые пригодятся для расчета регулятора промышленной установки  или другого реального объекта.

Исходные данные

Дана структурная схема одноконтурной системы автоматического регулирования четырёхканального объекта регулирования и передаточные функции объекта по всем его каналам.

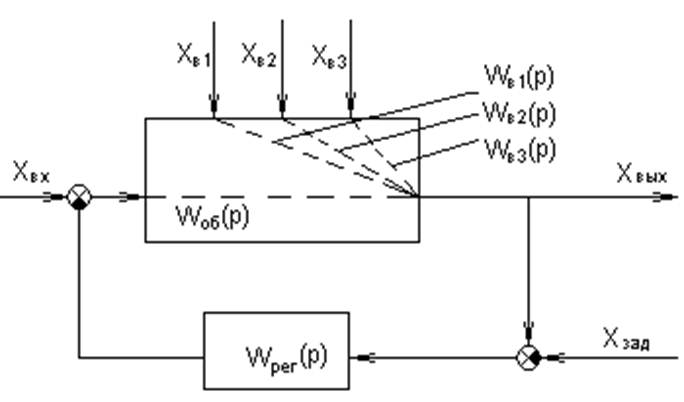
1. Канал регулирования:

- передаточная функция

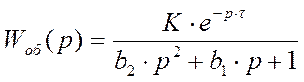
- передаточный коэффициент (коэффициент усиления)

K = 1,5

- время запаздывания

t = 2

- коэффициенты передаточной функции

b₁ =20

b₂ =75

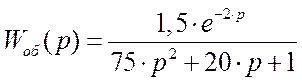
2. Канал возмущения 1:

- передаточная функция

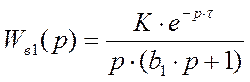
- передаточный коэффициент (коэффициент усиления)

K = 1

- время запаздывания

t = 0

- коэффициент передаточной функции

b₁ =1,5

    

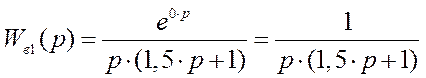
3. Канал возмущения 2:

- передаточная функция

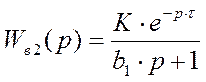
- передаточный коэффициент (коэффициент усиления)

K = 1

- время запаздывания

t = 0,5

- коэффициент передаточной функции

b₁ =5

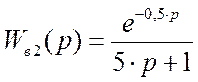
4. Канал возмущения 3:

- передаточная функция

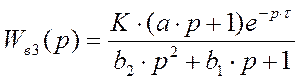
- передаточный коэффициент (коэффициент усиления)

K = 1

- время запаздывания

t = 5

- коэффициент передаточной функции

b₁ =32

b₂ =400

a =5

t =5

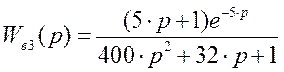
Часть 1. Расчет системы автоматического управления

с ПИ – регулятором для объекта, обладающего

запаздыванием в канале регулирования

Этап 1. Анализ динамических свойств объекта

во временной и частотной областях

1.1. Канал регулирования.

- построение переходной функции

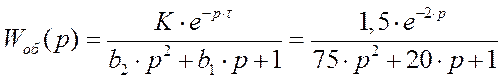
Так как запаздывание только сдвигает переходную функцию на время t, то вывод переходной функции будем делать для аналогичного звена без запаздывания, а «t» - учтем в окончательной формуле. Таким образом, передаточная функция объекта имеет вид:

W_об(p)=W_об⁰(p)×е^-pt

Х_вх(t)=1(t) – входной сигнал.

Изображение выходного сигнала имеет вид:

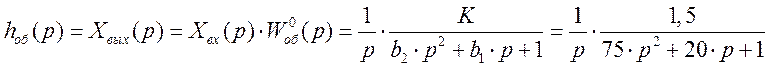
Рассмотрим характеристическое уравнение .

Найдем дискриминант: D = b₁² - 4×b₂ = 20² - 4×75 = > 0

Следовательно, корни характеристического уравнения действительные и разные:

  

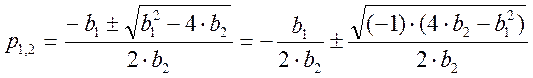
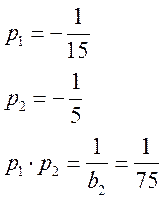
Т.к. корни характеристического уравнения действительные и разные, то полином можно разложить на множители  

Выводим переходную функцию.

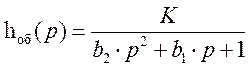
Разлагаем изображение на простые дроби:

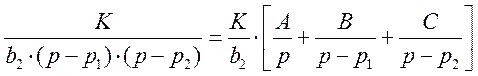
Определяем коэффициенты А, В, С:

A×p²- A×р₁p+ A×р₁p₂ - A×рp₂+B×p² - B×pр₂ +C×p²-Срр₁ = 1

при р²: А+В+С = 0

при р¹: -A×р₁ - A×р₂ - В×р₂ –Cр₁ = 0

при р⁰: A р₁p₂= 1

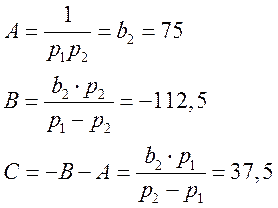
Оригинал будет:

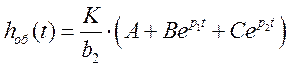
Подставим в оригинал выражения для А, В, С:

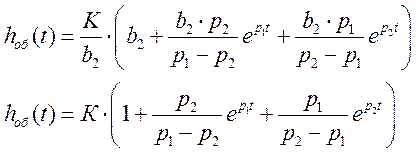
Учтем явление транспортного запаздывания, то есть при t ³ t переходная функция имеет вид:

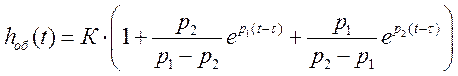
При   t < t   h(t) = 0.

Расчетные данные для построения переходного процесса в Таблице 1

Таблица 1

t	0	10	20	30	40	50	60	70	80	90	100	110
h(t)	0	0	0,05	0,16	0,31	0,47	0,62	0,74	0,85	0,93	0,99	1,03

t	120	130	140	150	160	170	180	190	200	210	220
h(t)	1,05	1,06	1,06	1,06	1,05	1,04	1,03	1,02	1,01	1,01	1,00

Рис. 1 Переходная функция объекта по каналу регулирования

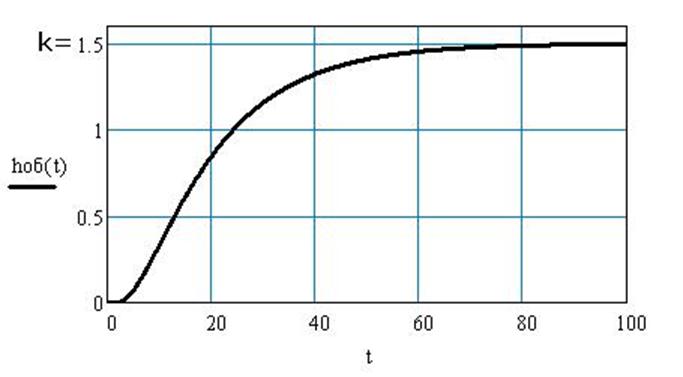
Так как звено колебательное, то переходный процесс носит не ярко выраженный колебательный характер. При окончании переходного процесса выходная величина выходит на установившееся значение, равное К=1,5. А так как передаточная функция включает в себя и передаточную функцию звена запаздывания, то переходная функция сдвигается вправо на величину запаздывания t = 2.

 - построение амплитудно-частотной характеристики

   

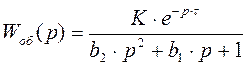
Заменяем  р = j×w             

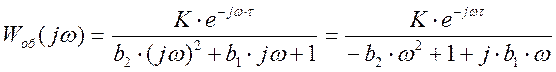
Находим выражение для АЧХ по каналу регулирования:

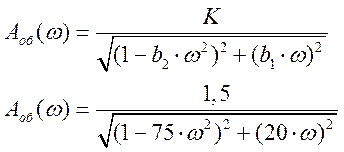
Расчетные данные для построения АЧХ в Таблице 2.

Таблица 2

w	0	0,01	0,011	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09	0,1
А(w)	1	1,452	1,446	1,374	1,274	1,164	1,053	0,947	0,849	0,79	0,68	0,609

w	0,11	0,12	0,13	0,14	0,15	0,16	0,17	0,2	0,5	0,6	0,65	0,69
А(w)	0,547	0,491	0,443	0,399	0,361	0,327	0,297	0,225	0,027	0,016	0,012	0,01

Рис.2 Амплитудно-частотная характеристика по каналу регулирования

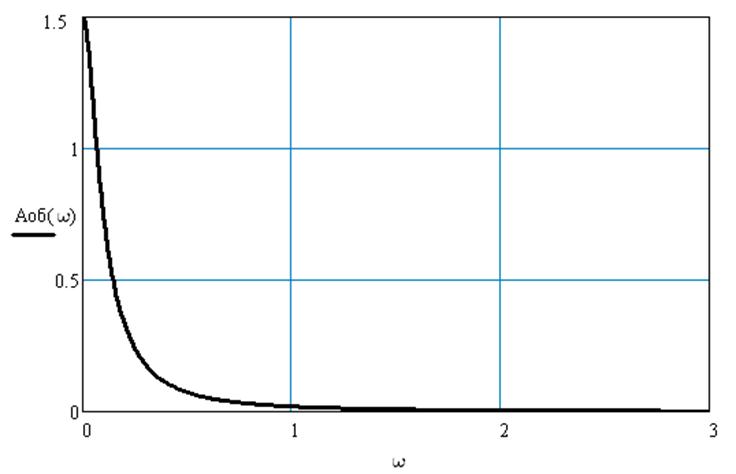
Объект по каналу регулирования является фильтром низких частот (т.е. хорошо пропускает низкочастотные воздействия и практически не пропускает высокочастотные).

- построение фазо-частотной характеристики

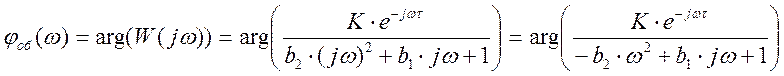
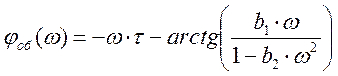
Пр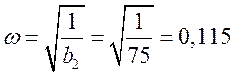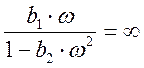и

 и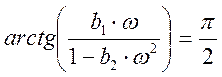  

Следовательно, при w  ≤  0,115

   

,

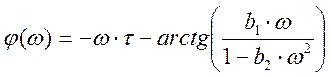
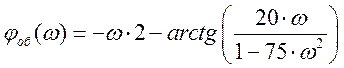а при w > 0,115

  

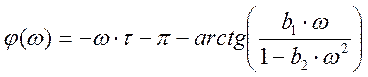
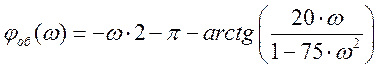
Расчетные данные для построения ФЧХ в Таблице 3

Таблица 3