Балаковский Институт Техники, Технологии и Управления.
Факультет: инженерно-строительный.
Кафедра УИТ.
Курсовая работа по дисциплине
Тема: “Анализ систем автоматического управления”.
студент группы УИТ-42
Алтухов А.А.
проверил преподаватель
Хречков Н.Г.
Балаково 2001.
Содержание.
Задание 1. Анализ линейной САУ 3
1.1. Вычисление эквивалентных передаточных функций разомкнутой и
замкнутой системы 4
1.2. Построение АФЧХ разомкнутой и замкнутой системы 6
1.3. Исследование устойчивости по критерию Гурвица 11
1.4. Определение запасов устойчивости 12
1.5. Построение переходного процесса САУ 12
1.6. Анализ качества управления 18
Задание 2. Анализ нелинейной САУ 19
2.1. Построение фазового портрета системы 20
2.2. Анализ и определение устойчивости системы управления 23
Задание 3 24
Задание 1. Анализ линейной САУ.
По заданной структурной схеме САУ вычислить эквивалентную передаточную функцию разомкнутой и замкнутой системы. Построить АФЧХ разомкнутой и замкнутой системы, исследовать устойчивость системы управления по одному из критериев. Определить запасы устойчивости системы по амплитуде и фазе. Построить переходный процесс в системе методом трапеций. По переходному процессу провести анализ качества управления и определить все его показатели. При необходимости дать рекомендации методов улучшения этих показателей.
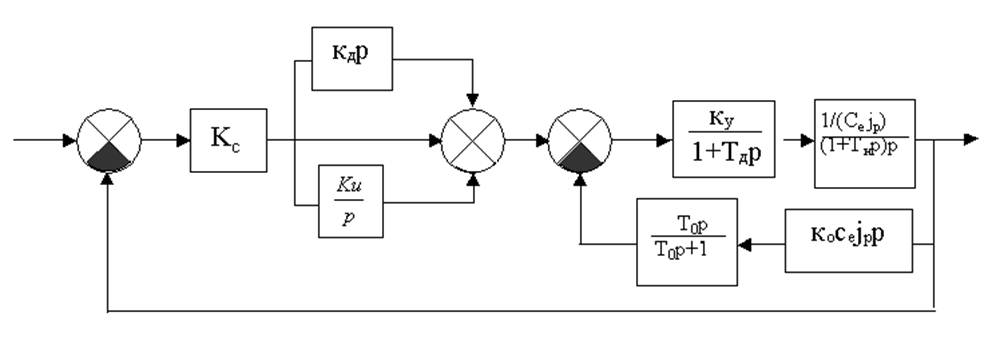
Рис.1 Исходная структурная схема линейной системы управления
Кс=0,86 Ко=0,69 Ку=127 Кд=0,27 Кu=2,3
Тм=0,43 Тд=0,017 То=0,07 Се=0,035 jр=94
1.1 Вычисление эквивалентных передаточных функций разомкнутой и замкнутой системы.
Упростим исходную структурную схему
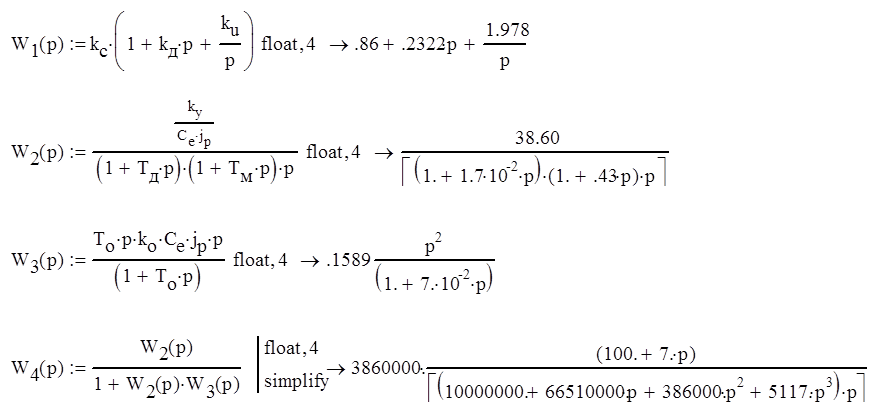
Передаточные функции разомкнутой и замкнутой системы будут иметь вид
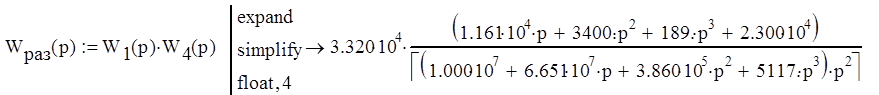
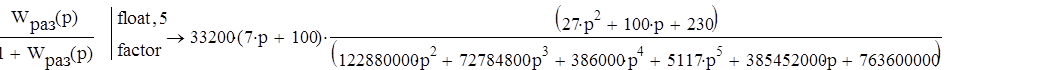
а упрощенная структурная схема

Рис.2. Упрощенная структурная схема.
Определим устойчивость системы по критерию Гурвица, используя характеристическое уравнение замкнутой системы
![]()
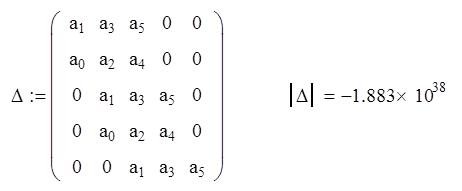
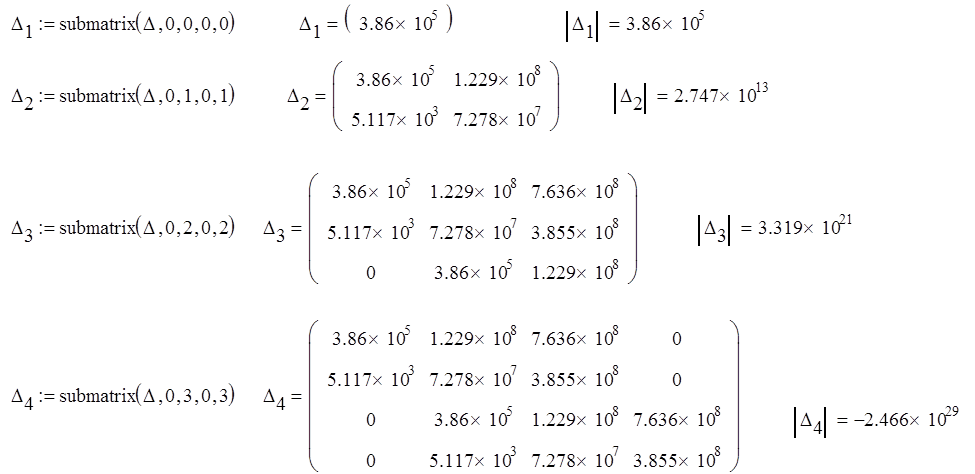
Так как среди определителей Гурвица есть отрицательные, система неустойчива.
Добьемся устойчивости системы подбором коэффициентов. Пусть То=0,04, получим
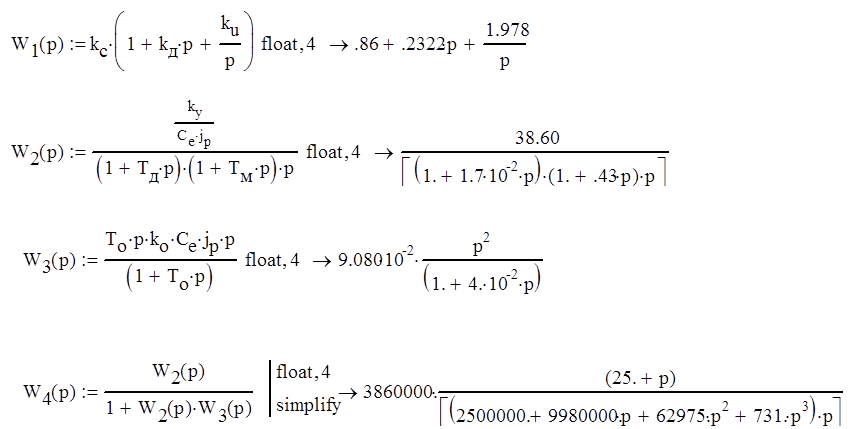
Передаточные функции разомкнутой и замкнутой системы примут вид
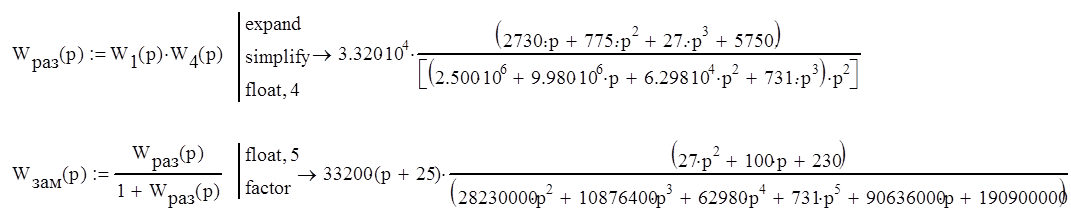
Представим передаточные функции разомкнутой и замкнутой
системы в виде функции комплексной переменной: ![]()
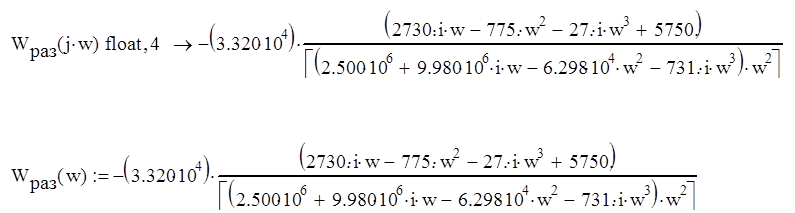
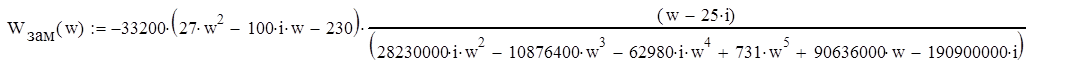
1.2. Построение АФЧХ разомкнутой и замкнутой системы.
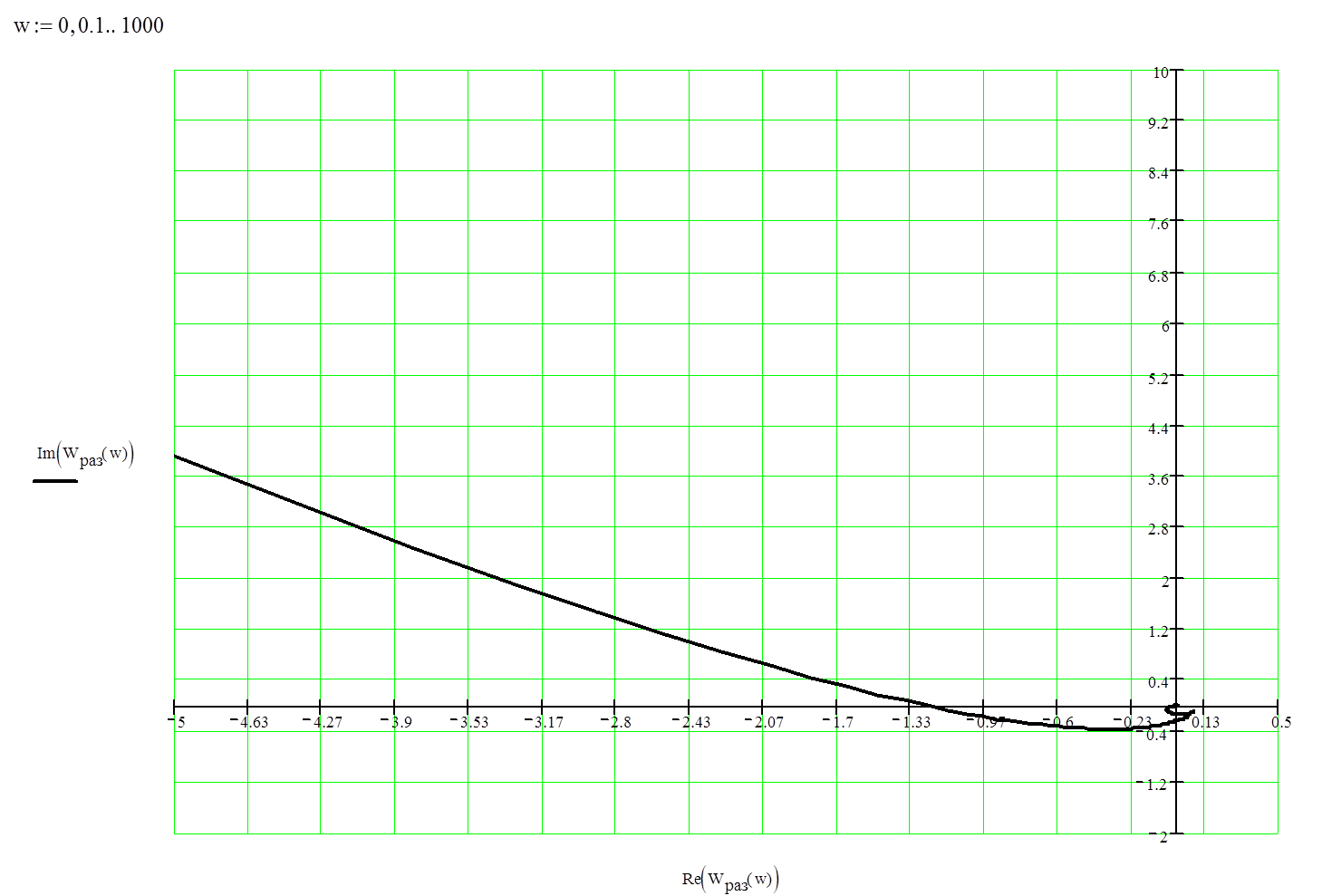 Рис. 3. АФЧХ разомкнутой системы.
Рис. 3. АФЧХ разомкнутой системы.
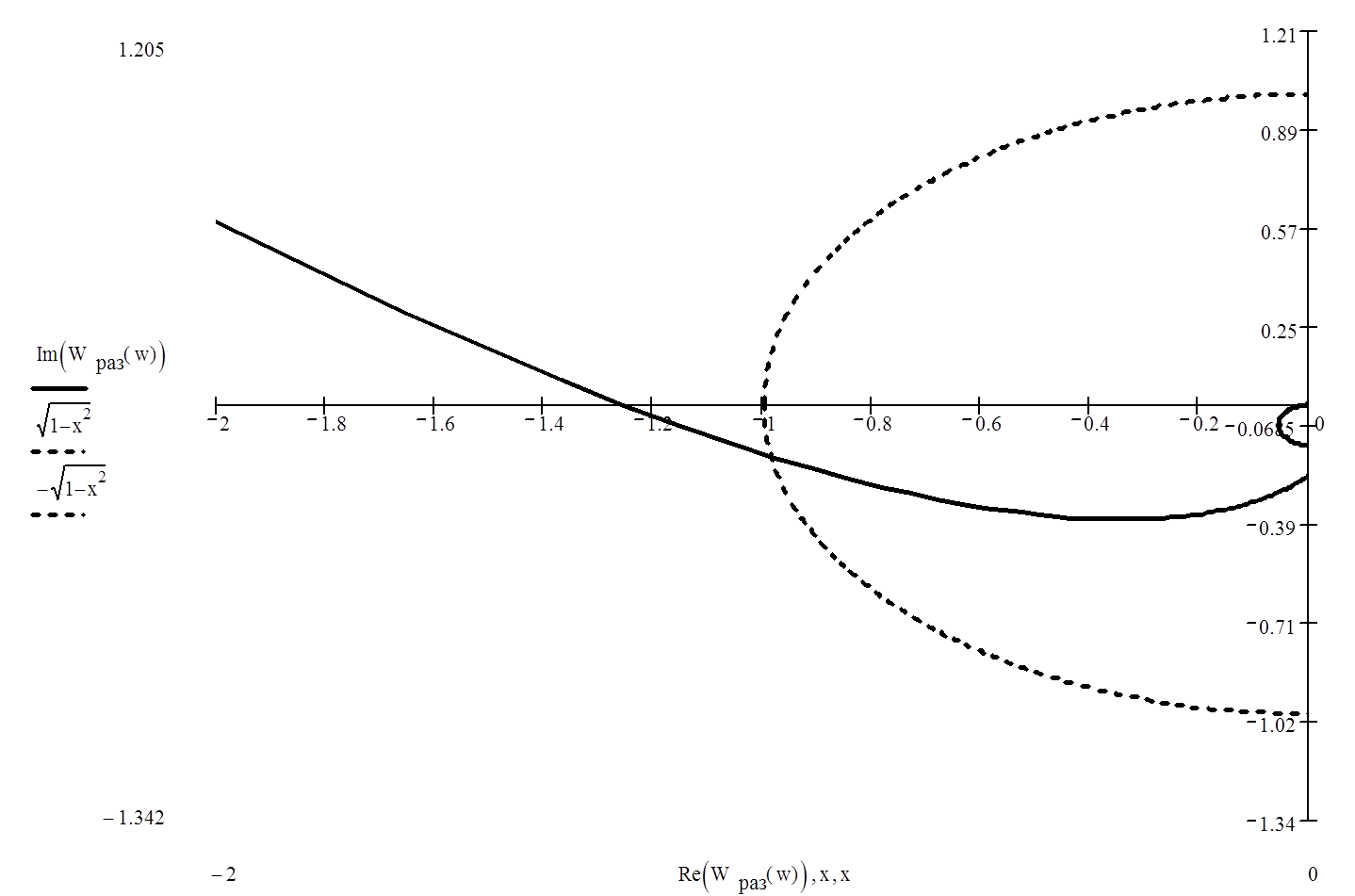
Рис. 4. Фрагмент АФЧХ разомкнутой системы вблизи начала координат
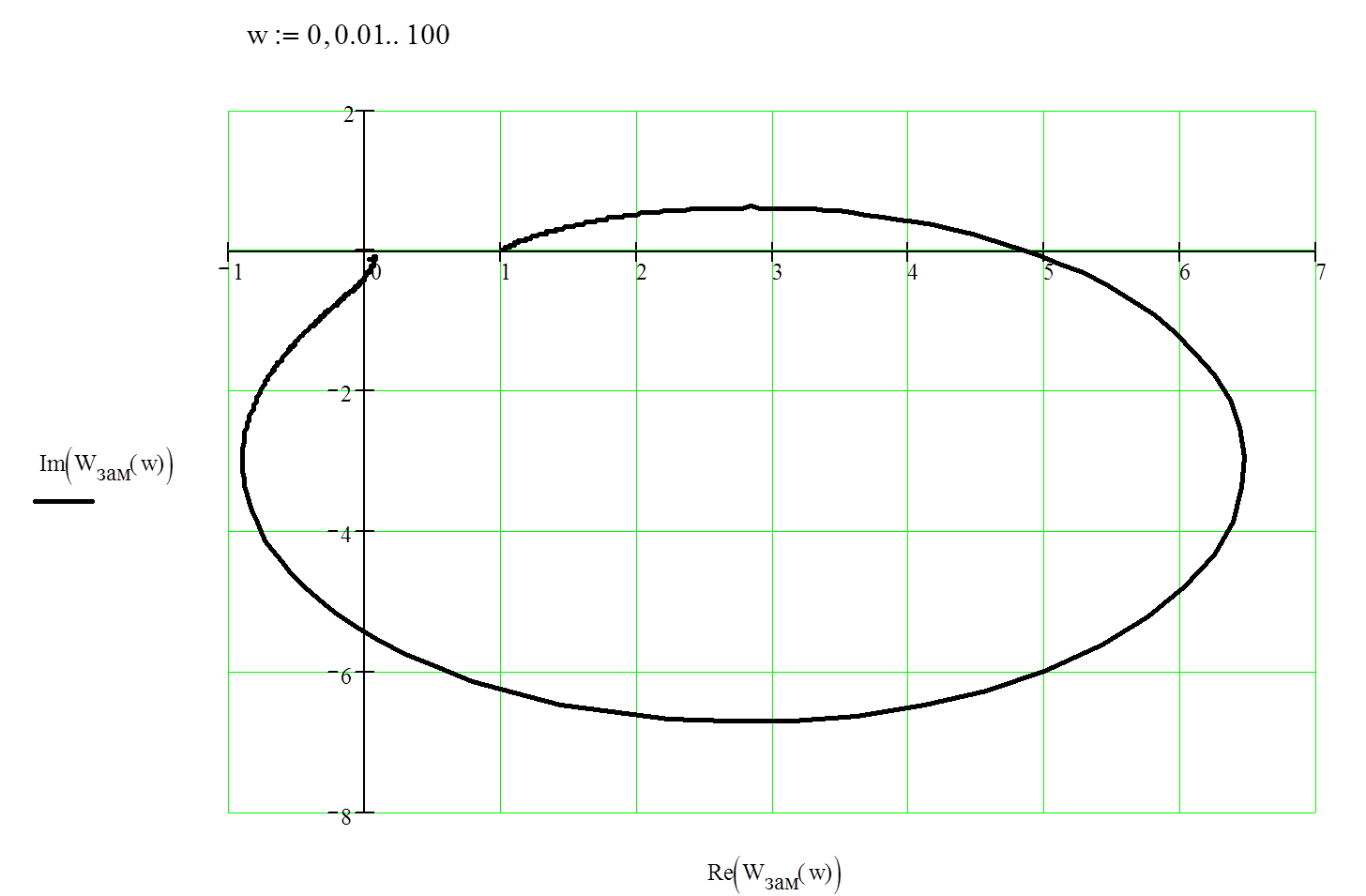
Рис. 5. АФЧХ замкнутой системы.


1.3. Исследование устойчивости по критерию Гурвица.
![]()
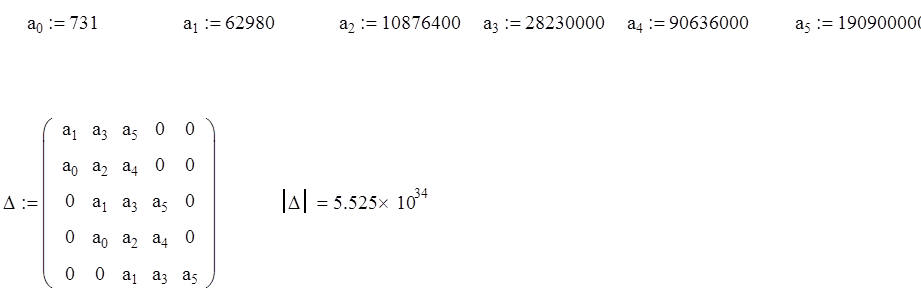
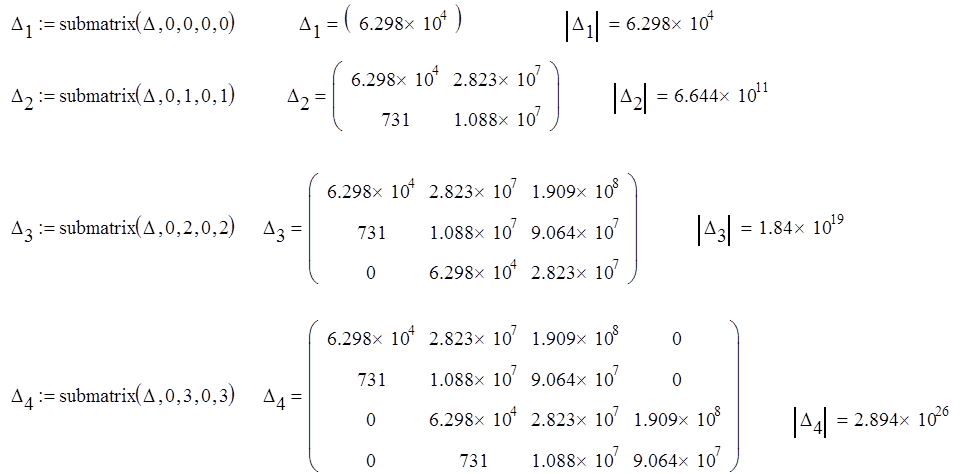
Так как все определители Гурвица положительны, система устойчива.
1.4. Определение запасов устойчивости
Запас устойчивости по фазе равен углу между отрицательной полуосью абсцисс и прямой, проведенной через начало координат и точку пересечения единичной окружности и АФЧХ.
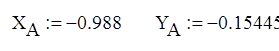
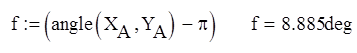
Запас устойчивости по фазе ![]()
Запас устойчивости по амплитуде равен длине отрезка
между точкой ![]() и точкой пересечения АФЧХ
разомкнутой системы с осью абсцисс.
и точкой пересечения АФЧХ
разомкнутой системы с осью абсцисс.
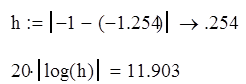
1.5. Построение переходного процесса САУ.
Зададим графически вещественную частотную функцию
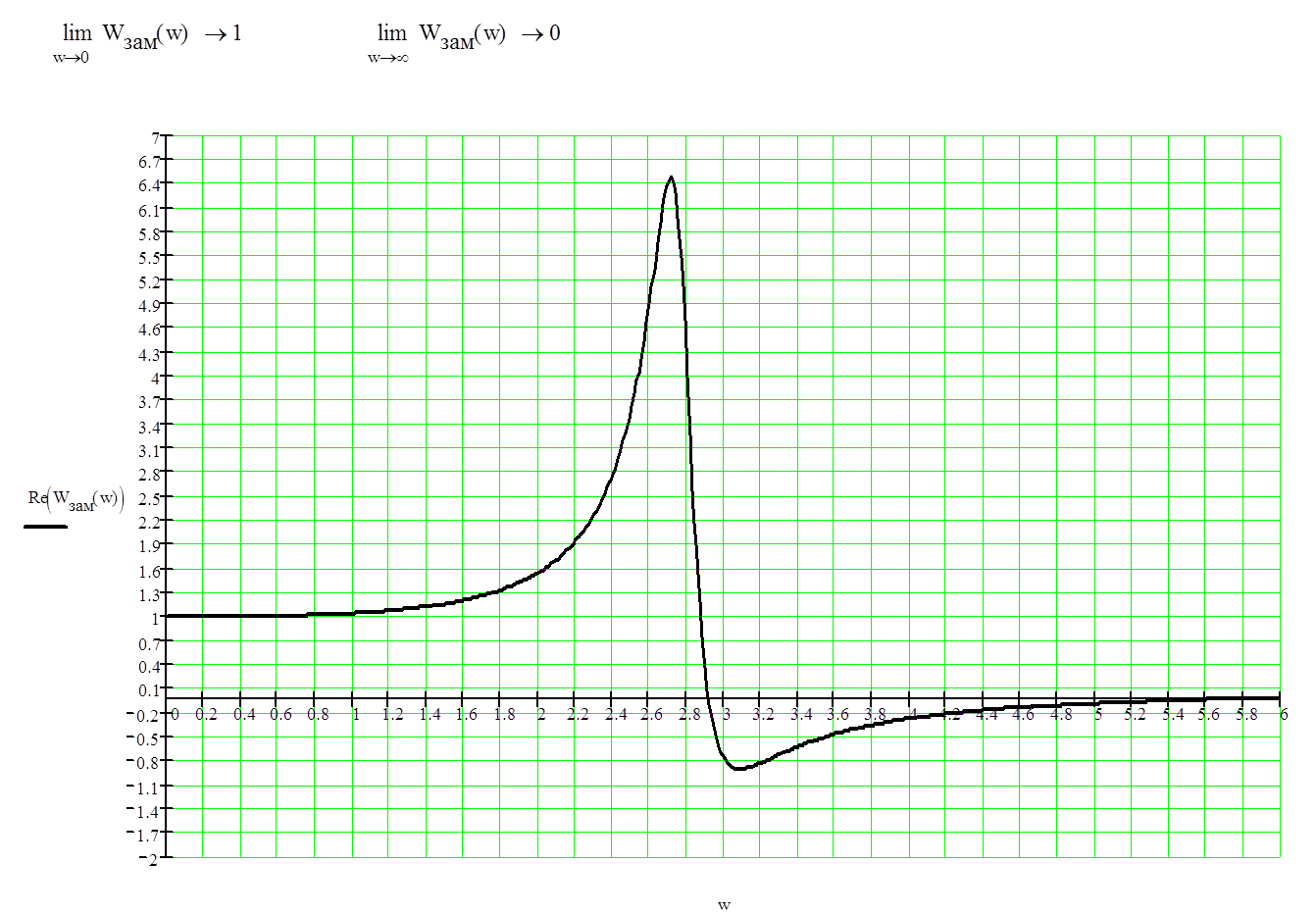
Рис. 6. Графическое изображение вещественной частотной характеристики.
Кривую ![]() заменили ломаной
линией так, чтобы образовать на чертеже фигуры в форме трапеции. По рис. 6
определяем для каждой трапеции величины нижнего основания
заменили ломаной
линией так, чтобы образовать на чертеже фигуры в форме трапеции. По рис. 6
определяем для каждой трапеции величины нижнего основания ![]() , верхнего основания
, верхнего основания ![]() , высоту
, высоту ![]() и
коэффициент
и
коэффициент 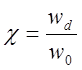 , определяющий форму трапеции:
, определяющий форму трапеции:
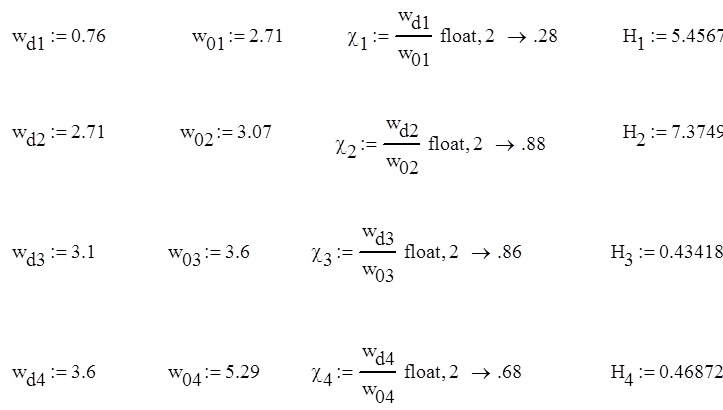
Задавая значения ![]() ,
по таблице находим
,
по таблице находим ![]() , зависящие от
, зависящие от ![]() :
:
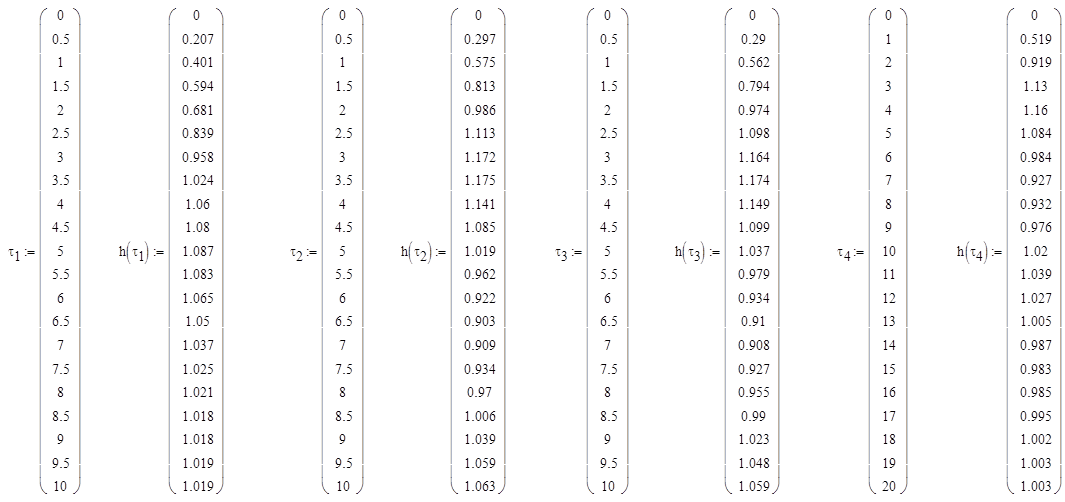
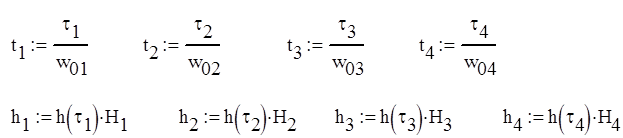
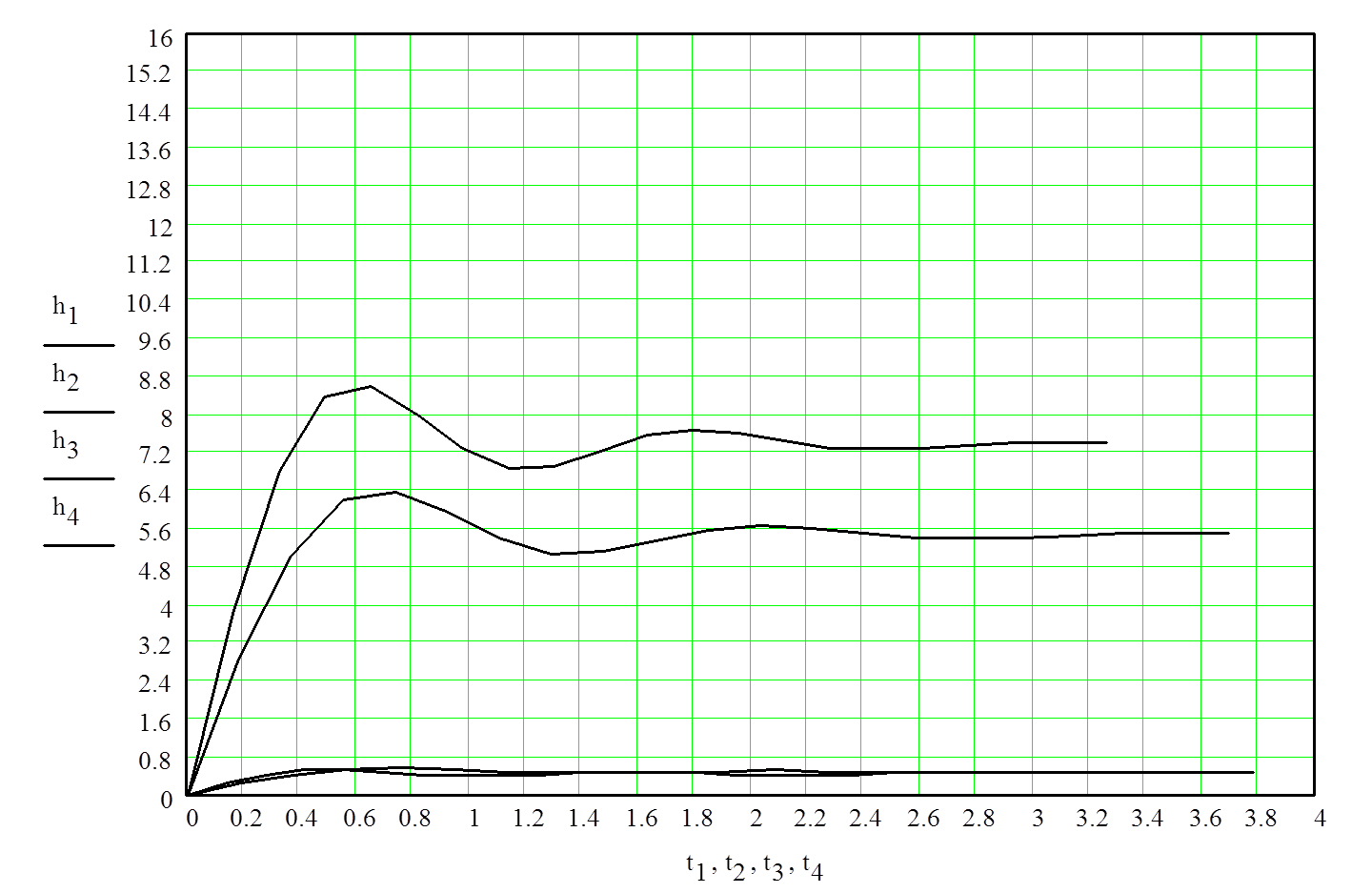
Рис. 7. График составляющих переходного процесса системы

Общий переходный процесс находим суммированием составляющих.
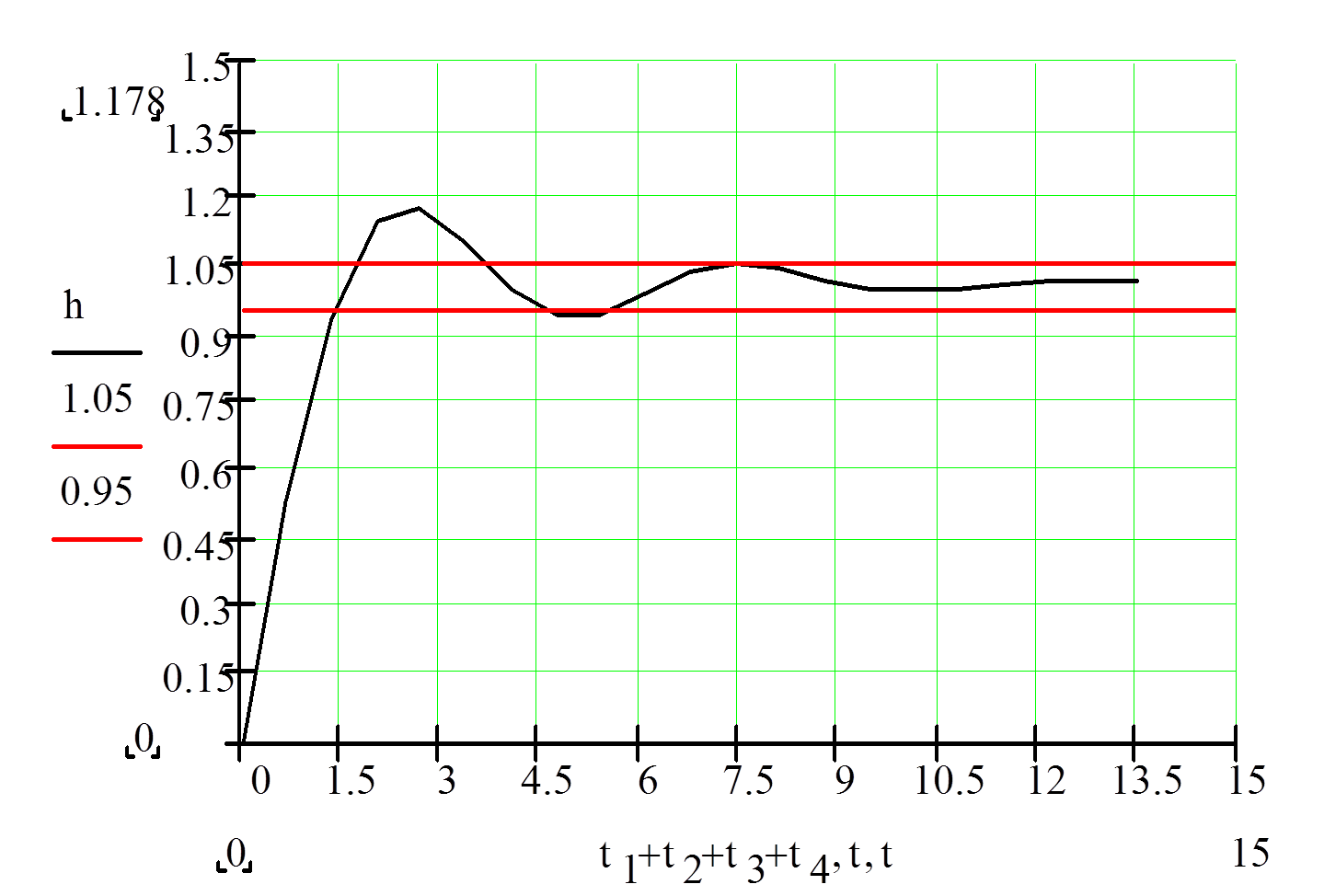
Рис. 8. График переходного процесса системы.
1.6. Анализ качества управления.
Установившееся значение переходного процесса ![]()
Время регулирования (достижения ![]() )
) ![]()
Время нарастания переходного процесса – время, при котором
график переходного процесса первый раз пересекает установившееся значение ![]()
Число колебаний ![]()
Максимальное значение переходного процесса ![]()
Минимальное значение переходного процесса ![]()
Перерегулирование 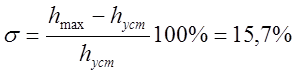
Декремент затухания 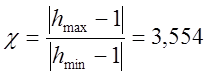
Период колебаний – время одного колебания ![]()
Частота колебаний 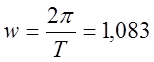 .
.
Вывод: проанализировав полученные результаты, видим, что данная САУ является устойчивой, переходный процесс завершается после 2-х колебаний. Система имеет достаточные для функционирования запасы устойчивости по амплитуде и фазе. Качество управления САУ требует дополнительной коррекции. Для уменьшения времени регулирования можно увеличить общий коэффициент усиления или уменьшить постоянную времени.
Задание 2. Анализ нелинейной САУ.
По заданной структурной схеме САУ построить ее фазовый портрет методом припасовывания. По фазовому портрету провести анализ системы управления, определить её устойчивость.

Рис. 9. Структурная схема нелинейной системы управления
То=11,8 К0=12,4 К1=0,38 К2=4,8 К3=0,007
аwср=0,5 Umax=110 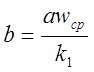
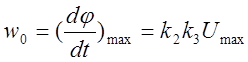
 |
2.1. Построение фазового портрета системы
Рассчитаем 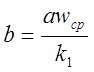 и
и 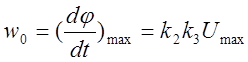
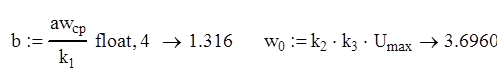
Упростим структурную схему нелинейной системы управления. Для этого сгруппируем все линейные и нелинейные звенья системы. Получим следующую структурную схему.
 |
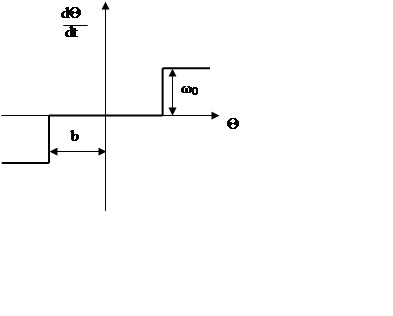
Рис. 11. Характеристика нелинейного элемента
где F(aw) – нелинейная часть СУ,
W(p) – линейная передаточная функция СУ.
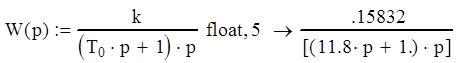
Фазовый портрет построим по формулам
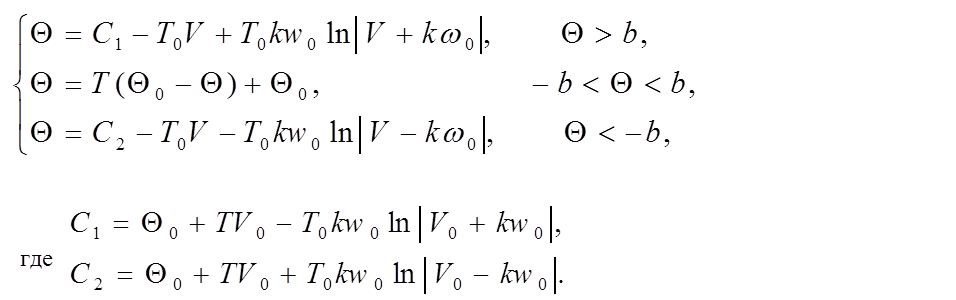
Далее приведен ход вычислений в системе Mathcad 2000.

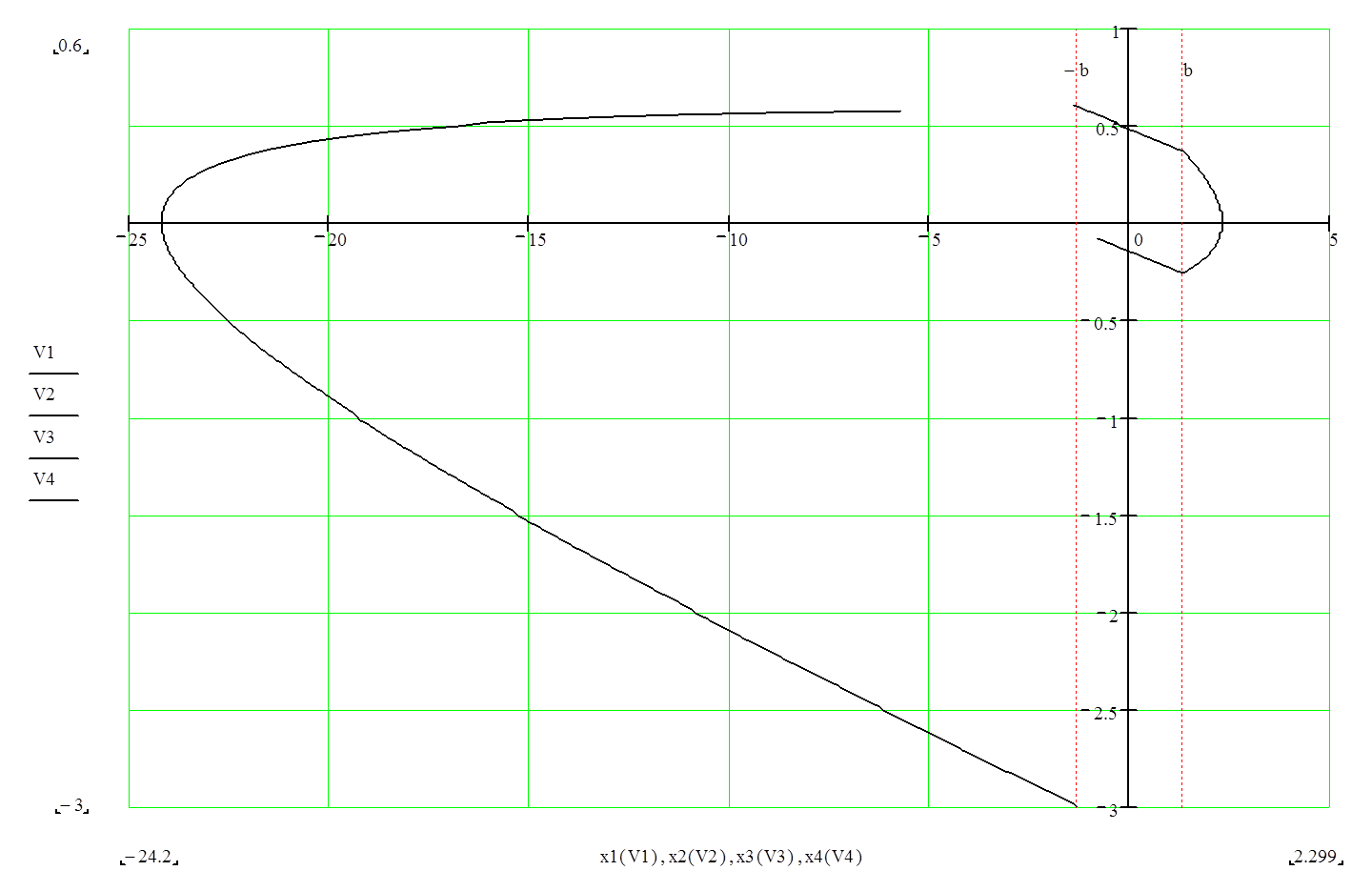
Рис. 12. Фазовый портрет системы управления.
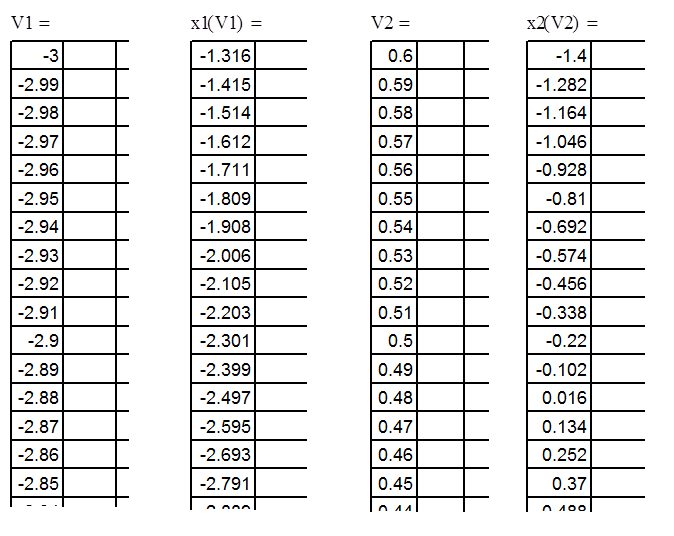
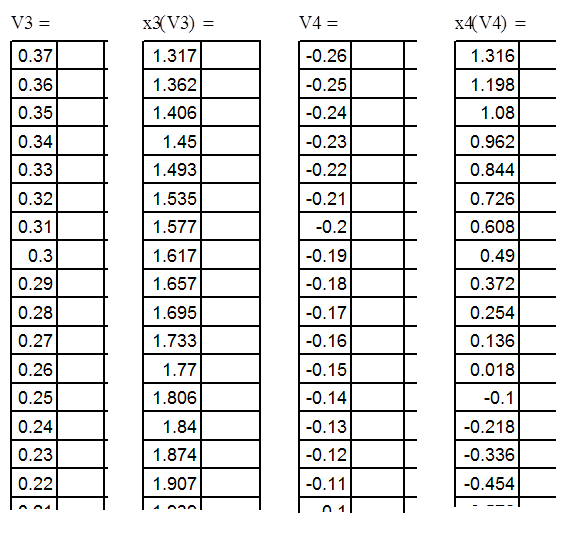
2.2. Анализ и определение устойчивости системы управления
Из фазового портрета видно, что система устойчива,
т.к. последняя составляющая графика пересекает ось ![]() на
отрезке
на
отрезке ![]() в точке –1,314. С этого момента
система блуждает с нулевой скоростью и неопределённостью от
в точке –1,314. С этого момента
система блуждает с нулевой скоростью и неопределённостью от ![]() до
до ![]() , что соответствует состоянию
устойчивости. Качество управления, судя по фазовому портрету, не является
удовлетворительным и требует коррекции.
, что соответствует состоянию
устойчивости. Качество управления, судя по фазовому портрету, не является
удовлетворительным и требует коррекции.
Задание 3.
От структурной схемы рис. 9 перейти к принципиальной схеме.
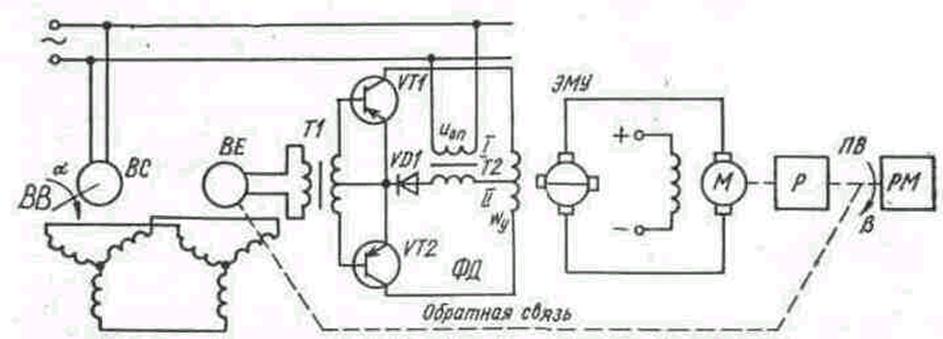
Рис. 13. Синхронно – следящая система.
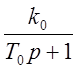 . М- двигатель
постоянного тока, Р – редуктор с передаточной функцией К3. Между редуктором и исполнительным механизмом
установлено интегрирующее звено
. М- двигатель
постоянного тока, Р – редуктор с передаточной функцией К3. Между редуктором и исполнительным механизмом
установлено интегрирующее звено Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.