Анализ нескорректированной системы автоматического управления

Содержание

Введение………………………………………………………………….…..……6

1.  Анализ структуры нескорректированной системы автоматического управления (САУ)……………………………………………….………….…7

1.1. Структурная схема нескорректированной САУ………………………...7

1.2. Передаточные функции разомкнутой системы………………………….7

1.3. Передаточные функции замкнутой системы………………………........9

2.  Анализ устойчивости нескорректированной САУ…………..………...……4

2.1. Критерий Гурвица………………………………………………………..14

2.2. Критерий Найквиста………………………………………………………4

2.3. Критерий Михайлова……………………………………………………..6

2.4. Анализ логарифмических частотных характеристик………….………18

3.  Анализ качества нескорректированной САУ………………………………21

4.  Синтез корректирующего устройства………………………………………21

4.1. Синтез корректирующего устройства методом Соколова…………….21

4.2. Анализ качества скорректированной САУ……………………………..24

4.3.  D-разбиение в области параметра одного параметра……………26

5.  Анализ скорректированной САУ при введении нелинейного элемента…29

5.1. Введение в прямой тракт скорректированной системы нелинейного элемента…………………………………………………….…………….29

5.2. Анализ абсолютной устойчивости нелинейной системы…….……….31

Заключение……………………………………………………………….……...33

Список литературы…………………………………………………….…….….34

Приложение………………………………………….…………………………..35

Введение

Теория систем автоматического управления (ТАУ) содержит в себе курс необходимы для анализа проектирования, изучения, моделирования и коррекции различного рода систем: таких как механические, гидравлические, электронные и так далее вплоть до биологических. Данная дисциплина позволяет оценить параметры системы различного рода: устойчива ли система, насколько точно система работает в заданном режиме. Так же курс ТАУ рассматривает анализ переходных процессов, который позволяет судить о быстродействии системы и других переходных характеристиках системы автоматического управления.

В рамках ТАУ рассматривается устойчивость линейных и нелинейных систем. Устойчивость линейной системы оценивается по различным критериям. Эти критерии можно разделить на алгебраические и частотные. К алгебраическим критериям относят критерий Гурвица, Рауса, к частотным – Найквиста, Михайлова и др. Абсолютную устойчивость нелинейных систем можно оценить с помощью критерия Попова.

Особенностью переходных процессов в нелинейных системах является возникновение незатухающих колебаний или автоколебаний. Они могут оказывать как отрицательное, так и положительное влияние на системы в целом. Условия возникновения автоколебаний рассматриваются в рамках частотного метода Гольдфарба.

Данная курсовая работа содержит анализ, коррекцию системы автоматического управления, а так же оценки ее качества и устойчивости.

1.Анализ структуры нескорректированной системы автоматического управления (САУ).

1.1.Структурная схема нескорректированной САУ.

Схема нескорректированной системы представлена на рис.1.1.

W2(s)

W1(s)

                                                                      f(t)

              g(t)                                                              x(t)

                                                                     

 

Рис.1.1 Схема нескорректированной системы

Передаточные функции звеньев данной системы имеют вид:

;

.

1.2.Передаточные функции разомкнутой системы.

Структурная схема разомкнутой системы при нулевом внешнем воздействии представлена на рис.1.2.

                                                                                 f(t)=0

W2(s)

W1(s)

                            g(t)                                                    x(t)

Рис.1.2

Эквивалентная передаточная функция системы, структурная схема которой изображена на рис.1.2, может быть выражена как

;

.

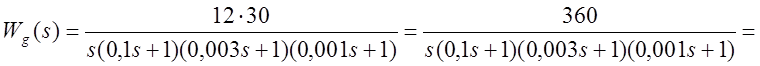
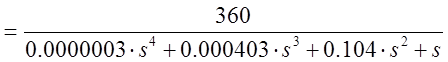Для изучения характеристик системы использовано моделирование в среде Matlab. На рис.1.3 представлена схема моделирования.

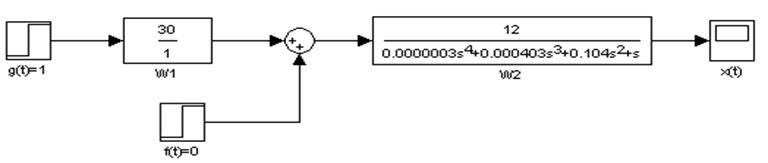
Рис.1.3

На выходе из системы получена переходная характеристика для разомкнутой системы при нулевом внешнем воздействии (рис .1.4).

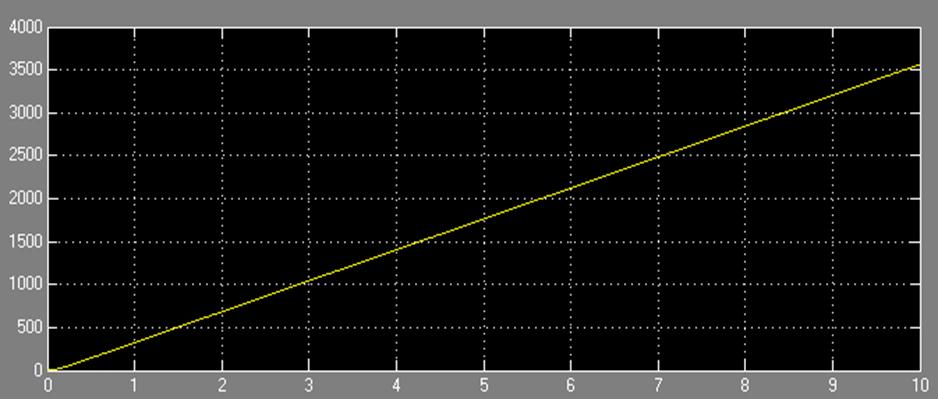Рис.1.4

Структурная схема разомкнутой системы при нулевом задающем воздействии представлена на рис.1.5.

                                                                       f(t)

W2(s)

W1(s)

                         g(t)=0                                             x(t)

 

Рис.1.5

Эквивалентная передаточная функция системы, структурная схема которой изображена на рис.1.5, может быть выражена как

;

.

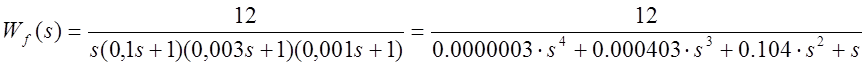На рис.1.6 представлена схема моделирования в Matlab.

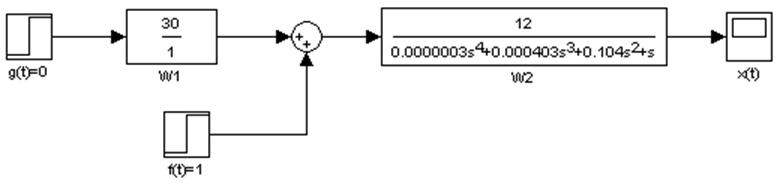
Рис.1.6

Переходная характеристика, полученная на выходе из системы при нулевом задающем воздействии, представлена на рис.1.7.

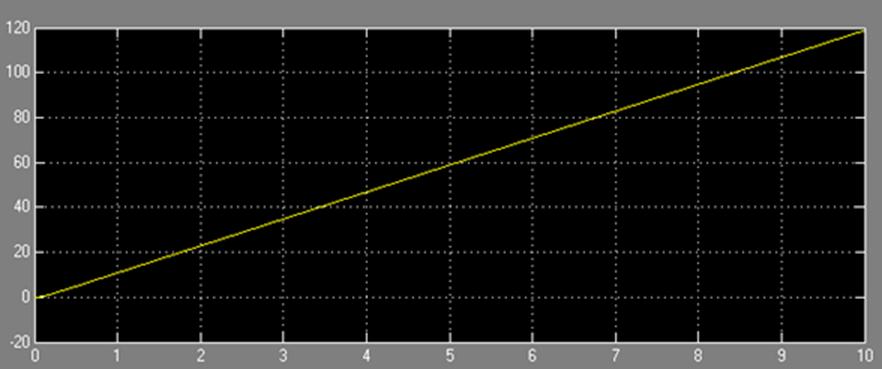
Рис.1.7

1.3.Передаточные функции замкнутой системы.

Структурная схема замкнутой системы при нулевом внешнем воздействии представлена на рис.1.8.

                                                             f(t)=0

 

W2(s)

W1(s)

               g(t)          ε(t)                                                          x(t)

 

Рис.1.8

Эквивалентная передаточная функция системы, структурная схема которой изображена на рис.1.8, может быть выражена как

;

.

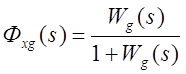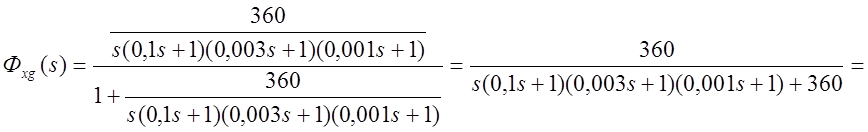
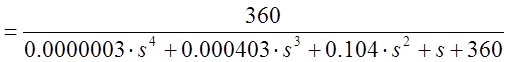Схема моделирования в Matlab представлена на рис.1.9

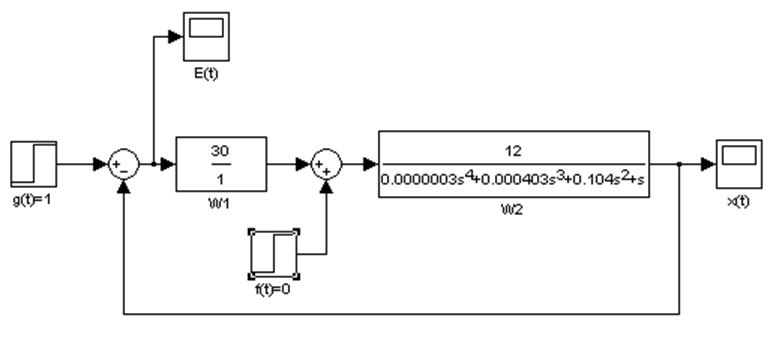
Рис.1.9

Переходная характеристика, полученная для замкнутой системы при нулевом внешнем воздействии, изображена на рис.1.10.

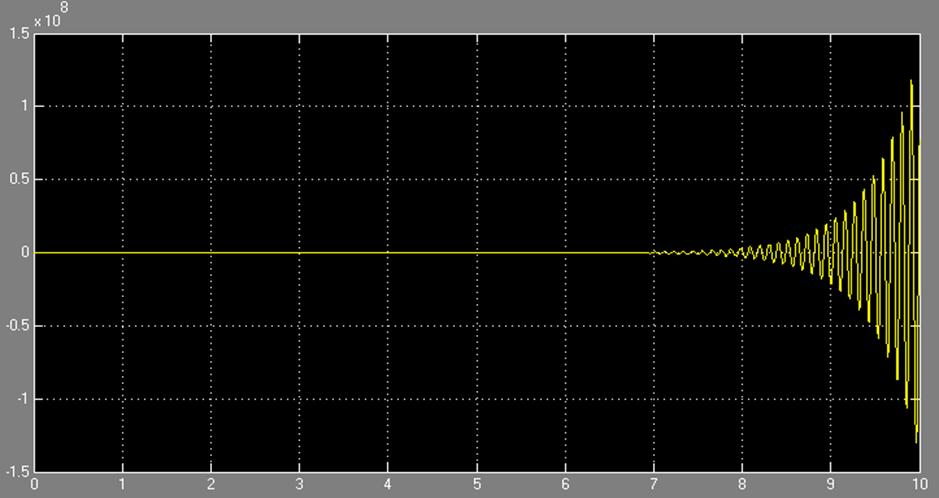
Рис.1.10.

Эквивалентная передаточная функция системы по ошибке, структурная схема которой изображена на рис.1.8, может быть выражена как

;

.

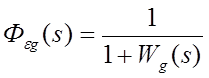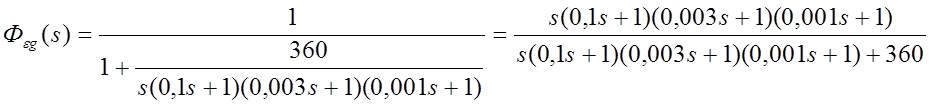
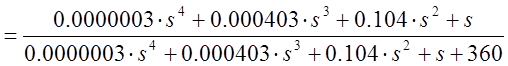Характеристика, иллюстрирующая изменение значения ошибки от времени изображена на рис.1.11

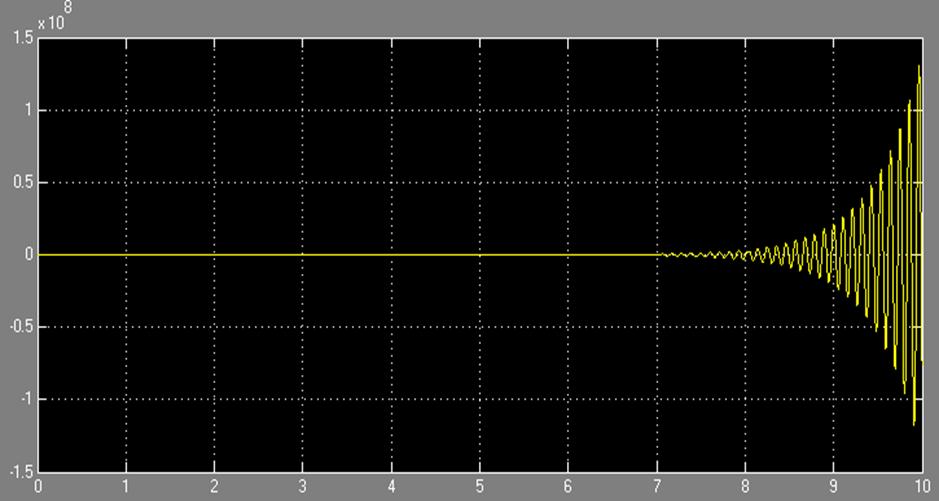
Рис.1.11

Структурная схема замкнутой системы при нулевом задающем воздействии представлена на рис.1.12.