Другие предметы \ Теория автоматического управления

Анализ нескорректированной системы автоматического управления, страница 3

 Переход от Фн(р) к Фж(s) производится на основании теоремы масштабов преобразования Лапласа с использованием следующего соотношения

p=sz,

            

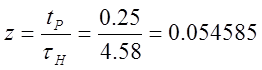
Желаемую передаточную функцию можно получить, из равенства

Фж(s)=Фн(sz)

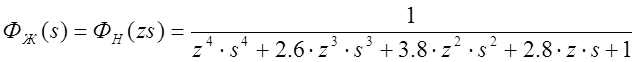
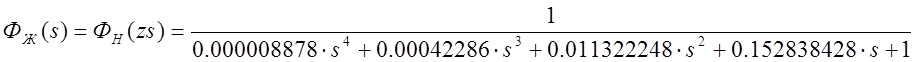
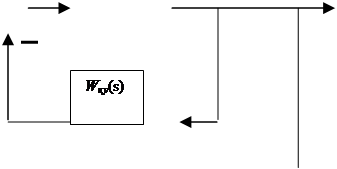
Структурная схема скорректированной системы изображена на рис.4.2. Н определить передаточную функцию корректирующего устройства (КУ).

                                                                                f(t)

W2(s)
 

 W1(s)
 
               g(t)                                                                                  x(t)

 


рис.4.2

Для упрощения вычислений вначале нужно записать эквивалентную передаточную функцию объекта управления и КУ.

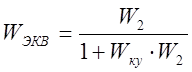
Передаточная функция скорректированной системы запишется как

;

;

;

.

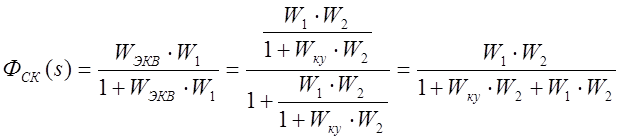Откуда можно выразить передаточную функцию корректирующего устройства

;

       

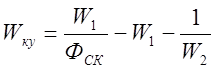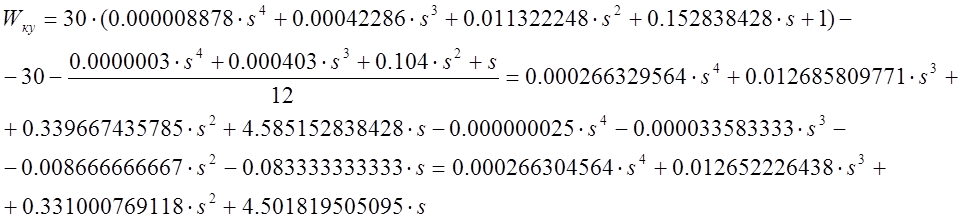
При подстановке исходных данных выражение  примет вид

.

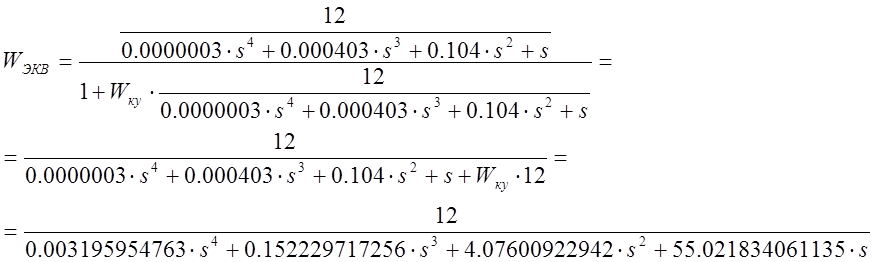4.2.Анализ качества скорректированной САУ.

Переходная характеристика скорректированной системы изображена на рис.4.3

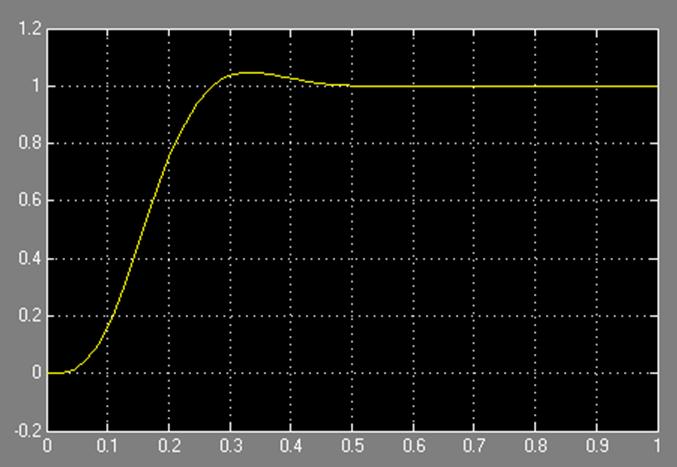
Рис.4.3

Время регулирования и перерегулирование численно равны

tрег=0.25 c    s=4.23 %.

Полученные значения удовлетворяют требованиям к синтезируемой системе.

Оценка запасов устойчивости по модулю и по фазе путем построения ЛАХ и ЛФХ (рис.4.4)

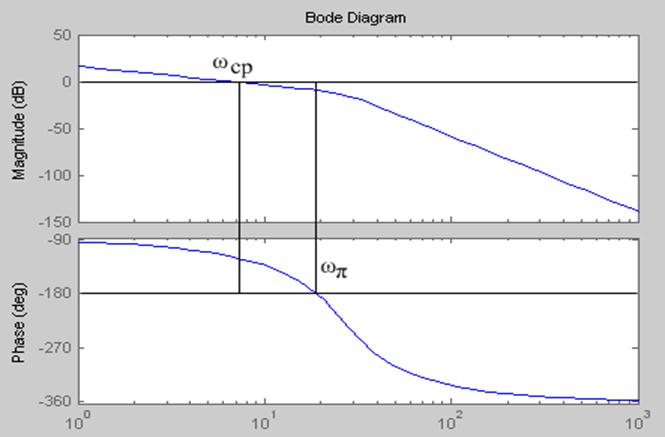
рис.4.4

По рис.4.5 определяют запасы устойчивости по модулю и по фазе, а так же ωπ и ωср

           

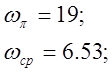
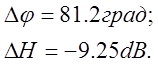
Система устойчива так как .

Определение коэффициентов ошибок.

С помощью MatLab можно определить значение коэффициентов ошибок:

;

;

.

Полученные коэффициенты ошибок отличаются от заданных, потому что в качестве главного критерия при формировании передаточной функции желаемой системы выступало минимальное время регулирования.

4.3.D-разбиение в области одного параметра.

Метод D-разбиения заключается в определении допустимой области изменения одного или нескольких параметров, при условии, что система не потеряет свою устойчивость.

Во-первых, необходимо записать передаточную функцию замкнутой системы и характеристичное уравнение

;

;

.

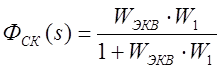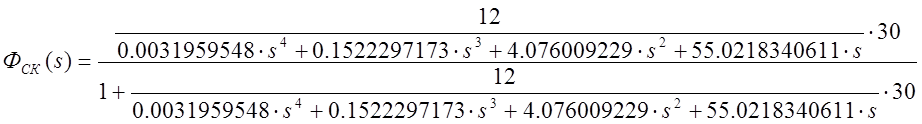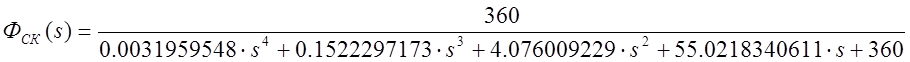Передаточная функция скорректированной системы в общем виде

.

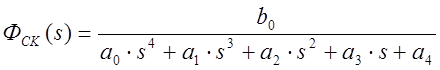Характеристическое уравнение имеет вид

.

Во-вторых, необходимо выразить  через остальные параметры

;

.

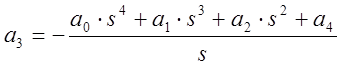При  s→jω выражение примет вид

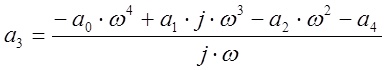
После постановки выпажени примет вид

.

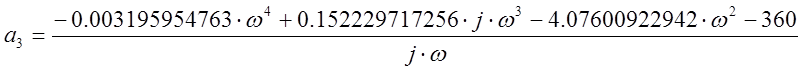Кривая D-разбиения в области параметра  изображена на рис.4.5

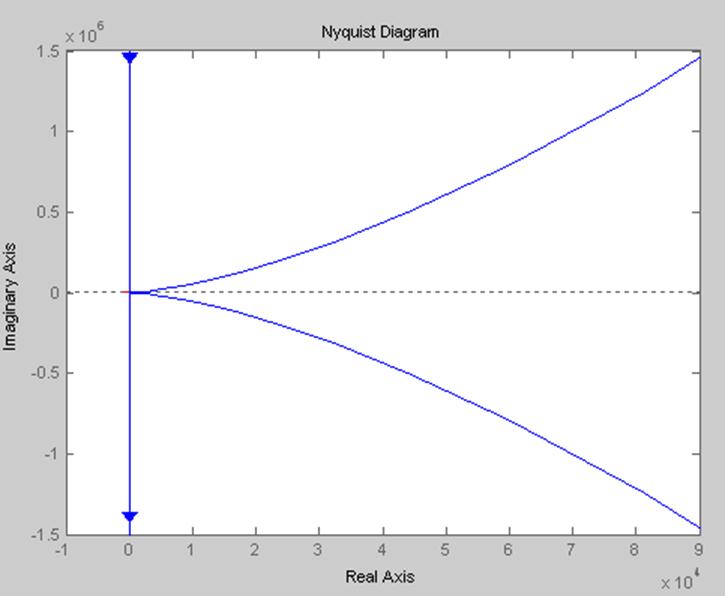
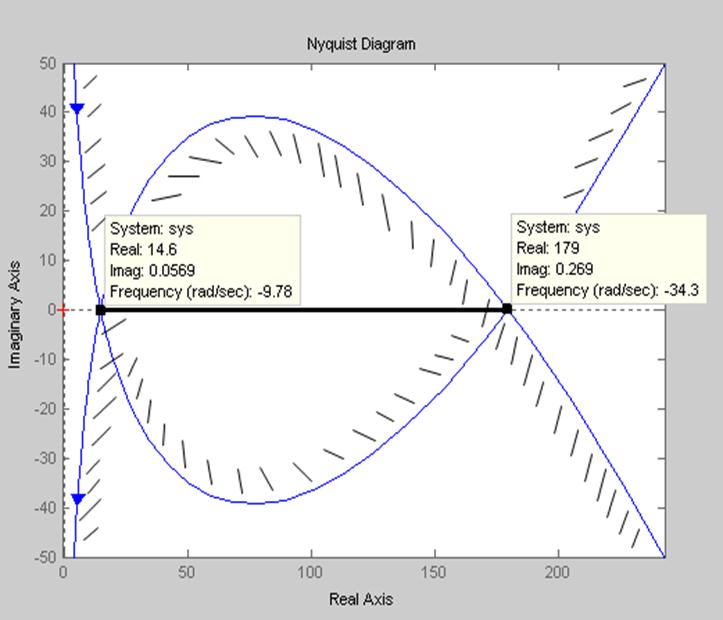
Рис.4.5

Так как параметр  должен принимать только действительные значения, то в полученной области необходимо выбрать только те значения, при которых Im()=0.

 Область значений:

 

Необходимо проверить, будет ли являться данный диапазон областью устойчивости, приняв  равным любому значению из данного диапазона.

Пусть . Передаточная функция замкнутой системы примет вид:

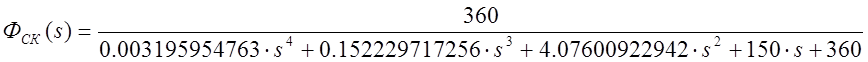
Требуется проверить устойчивость данной системы по любому из критериев устойчивости. На рис.4.6 изображен годограф скорректированной системы в разомкнутом виде.

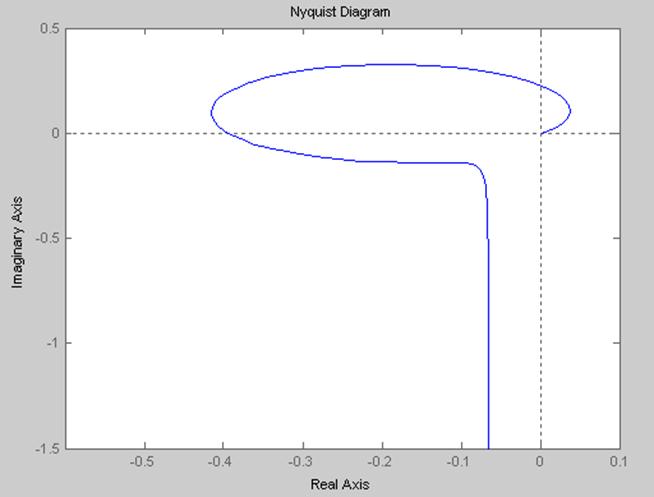
Рис.4.6

Годограф не охватывает точку (–1; j0). Система устойчива по Найквисту.

5.Анализ скорректированной САУ при введении нелинейного элемента.

5.1.Введение в прямой тракт скорректированной системы нелинейного элемента.      

В качестве нелинейного элемента выступает частный случай нелинейности типа насыщение и зона нечувствительности (рис.5.1).

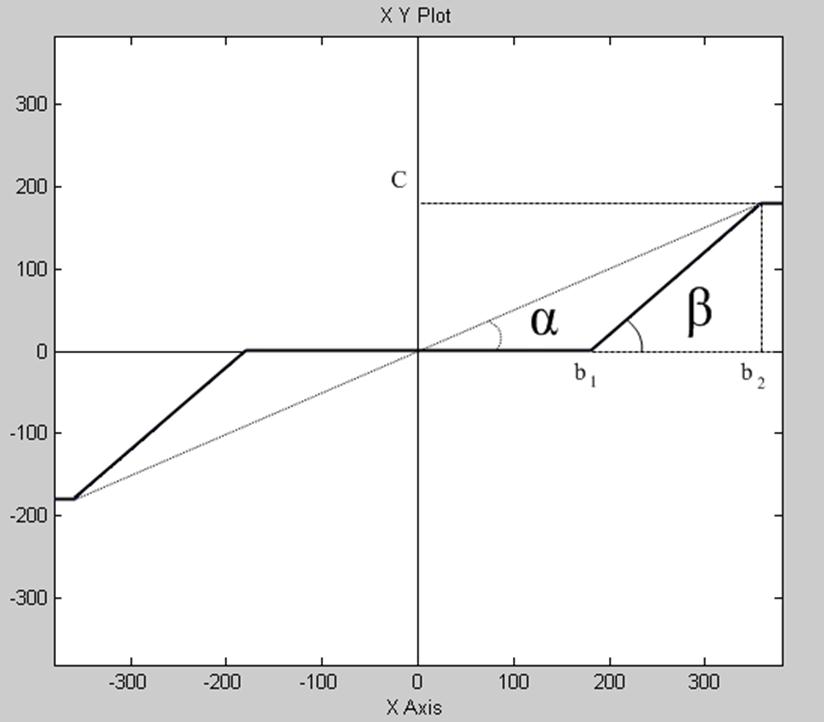
Рис.5.1

Параметры нелинейности:

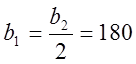
Коэффициенты гармонической линеаризации:

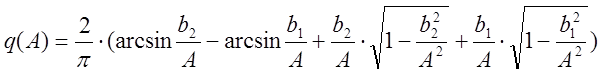
Используя метод Гольдфарба, составляют выражения для обратного инверсного коэффициента.

-

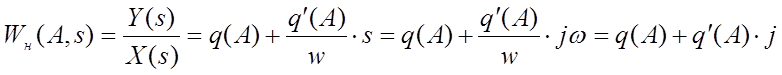
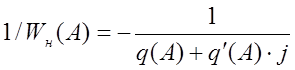
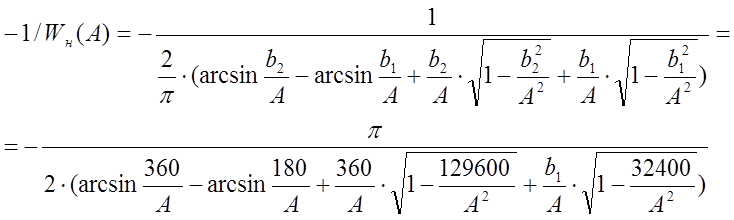
Затем определяют передаточную функцию линейной части

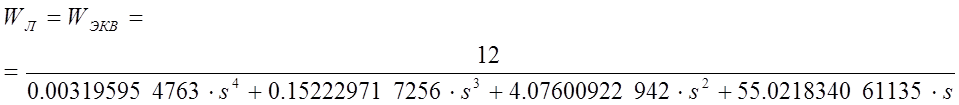
Для оценки возникновения автоколебаний выполняют построение АФХ линейной части и обратного инверсного коэффициента в одной плоскости (рис.5.2).

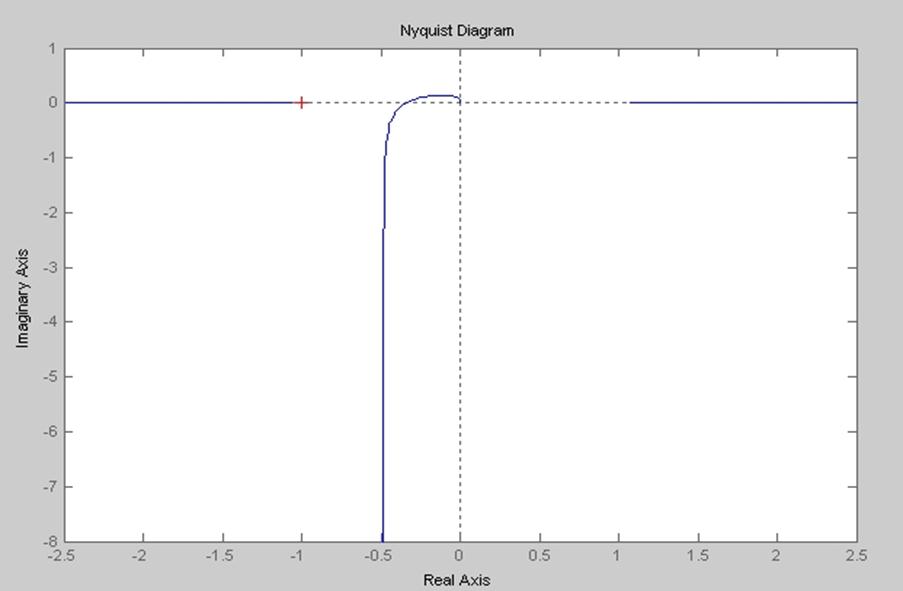
ГОЛЬД

Рис.5.2

Как видно АФХ линейной части и обратного инверсного коэффициента не пересекаются, что говорит о невозможности возникновения  автоколебаний.

5.2.Анализ абсолютной устойчивости нелинейной системы.

Критерий Попова: нелинейная система абсолютно устойчива, если модифицированный годограф весь находится правее прямой проходящей через точку (-1/k ;  j0).

Согласно критерию Попова необходимо привести передаточную функцию линейной части к виду:

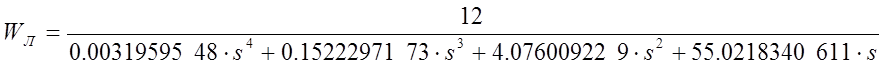
При s→jω выражение примет вид:

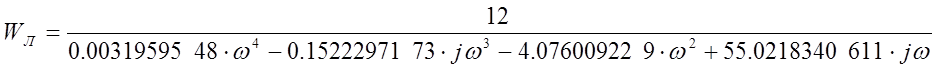
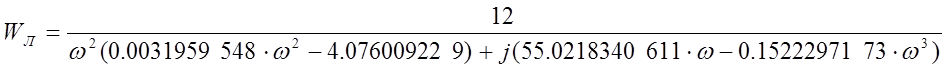
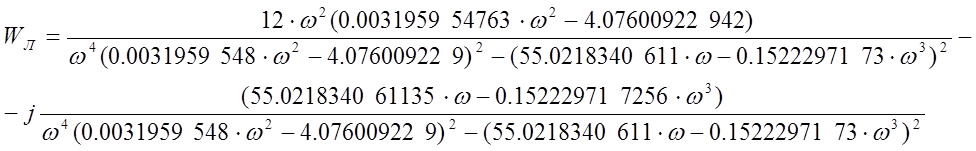          Затем модифицируют полученное выражение, умножив мнимую часть на ω

Далее выполняют построение АФХ для модифицированной передаточной функции (рис.5.3)

 

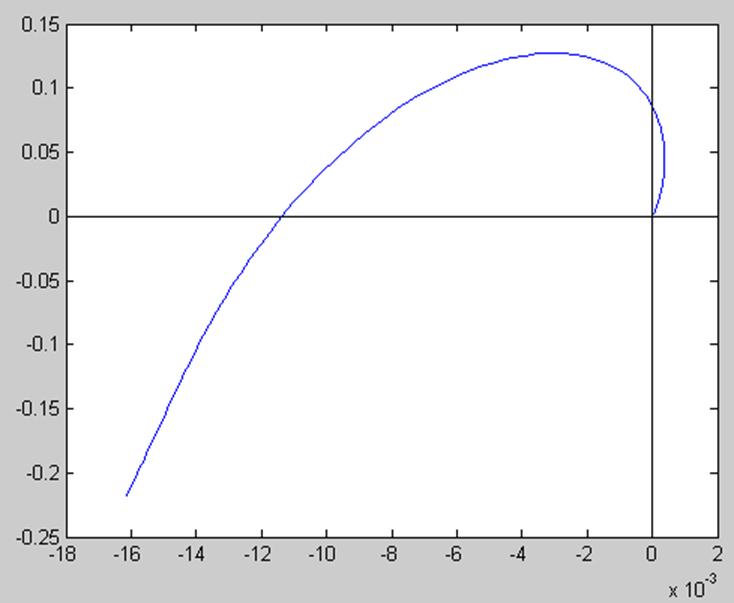
Рис.5.3

Как  видно из данного рисунка, существует возможность проведения хотя бы одной прямой через точку (-2; j0) левее модифицированного годографа, что указывает на абсолютную устойчивость нелинейной системы.

Заключение

В ходе выполнения данной курсовой работы был проведен анализ нескорректированной системы автоматического управления. Были рассмотрены передаточные функции разомкнутой и замкнутой систем.

Произведен анализ устойчивости системы по трем критериям. Нескорректированная САУ оказалась неустойчивой.

Анализ качества показал полную нестабильность системы. Переходные процессы нескорректированной САУ имели расходящийся колебательных характер.

Был произведен синтез корректирующего устройства методом Соколова. Основным требованием к синтезируемой системе стало минимальное время регулирования. На этой основе получена передаточная функция корректирующего устройства.

Анализ качества скорректированной системы показал, что переходные характеристики соответствуют требованиям к синтезируемой системе. Полученная система имеет положительные запасы устойчивости как по модулю, так и по фазе.

В результате оценки влияния на устойчивость системы одного из ее параметров, была определена область устойчивости системы для данного параметра.

Методом Гольдфарба было определено, что при введении в прямой тракт скорректированной системы автоколебаний не возникает, а частотный критерий Попова показал, что система при этом абсолютно устойчива.

Список литературы

1.  Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. – СПб.:Профессия, 2003. – 744 с.

2.  http://www.tehnoinfa.ru/teorijasistempravlenija/108.html

Скачать файл