Анализ нескорректированной системы автоматического управления, страница 2

W2(s)

                  f(t)                                                                    x(t)

 

W1(s)

                                                                   ε(t)  

 

                                                                                             g(t)=0

Рис.1.12

Эквивалентная передаточная функция системы, структурная схема которой изображена на рис.1.12, может быть выражена как

;

.

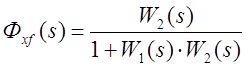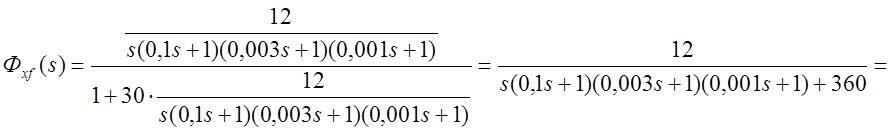
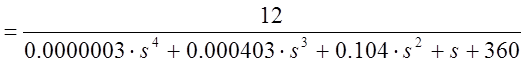Схема моделирования в Matlab представлена на рис.1.13

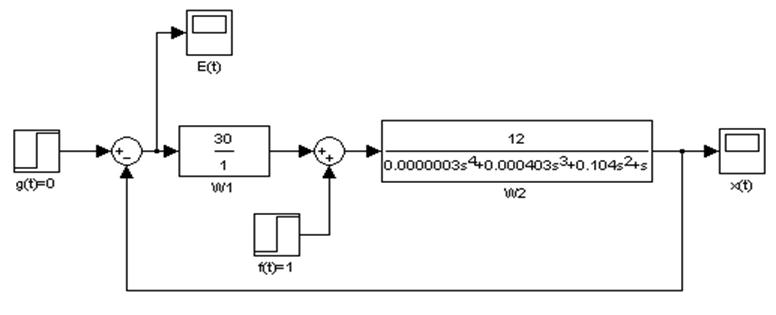
Рис.1.13

Переходная характеристика замкнутой системы при нулевом задающем воздействии изображения на рис.1.14.

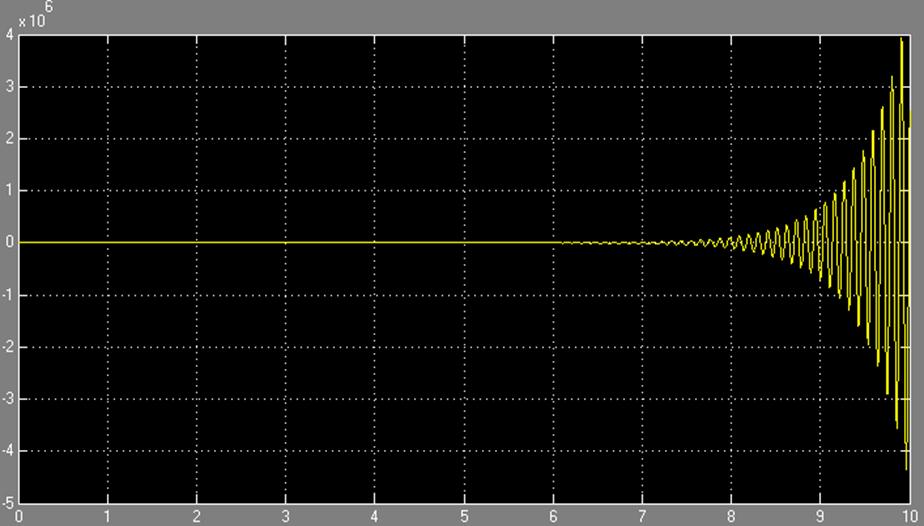
Рис.1.14

Структурная схема замкнутой системы при нулевом задающем воздействии представлена на рис.1.15. Выходной сигнал – ошибка.

                                                                                g(t)=0

W2(s)

                  f(t)                                                                    ε(t)  

 

Рис.1.15

Эквивалентная передаточная функция системы по ошибке, структурная схема которой изображена на рис.1.15, может быть выражена как

;

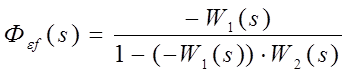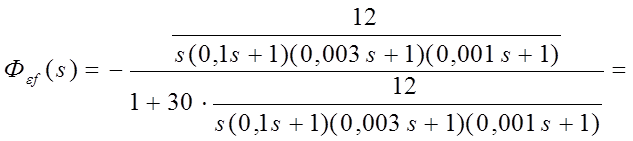
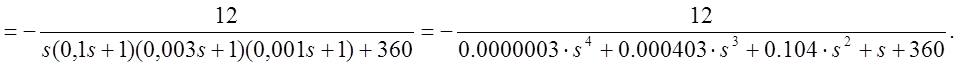
Переходная характеристика ошибки замкнутой системы изображена на рис.1.16.

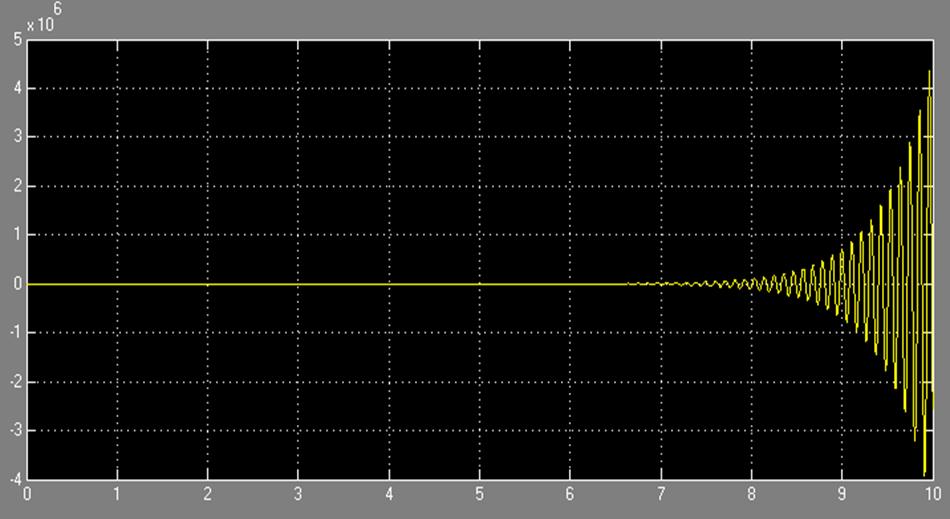
Рис.1.16

В ходе анализа структуры нескорректированной САУ были получены передаточные функции и переходные характеристики в разомкнутом и замкнутом состоянии.

2.Анализ устойчивости нескорректированной САУ.

2.1.Критерий Гурвица.

Алгебраический критерий Гурвица звучит следующим образом: необходимым и достаточным условием устойчивости замкнутой САУ будет выполнение условия, согласно которому все определители матриц составленных из коэффициентов характеристического уравнения должны иметь тот же знак что и b₀.

Передаточная функция замкнутой системы имеет вид

.

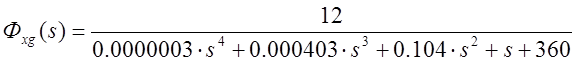Характеристическим полиномом замкнутой системы является знаменатель ее передаточной функции

.

Из полученного характеристического полинома определяют коэффициенты

b₀=0.0000003,    b₁=0.000403,    b₂=0.104,   b₃=1,   b₄=360.

      b₀>0

 

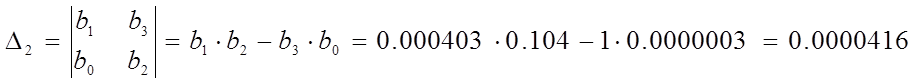
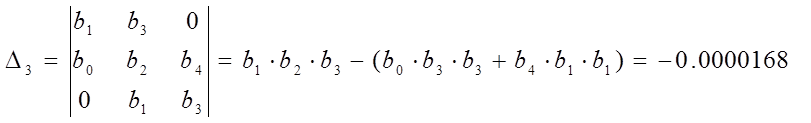
Условие устойчивости по критерию Гурвица не выполняется. Система не устойчива.

2.2.Критерий Найквиста.

Замкнутая система устойчива, если при изменении частоты от 0 до +∞ годограф передаточной функции разомкнутой САУ охватывал точку (–1 ,j0)    λ/2 раз, вращаясь в положительном направлении.

В рамках критерия Найквиста рассматривают передаточную функцию разомкнутой системы, которая имеет вид

.

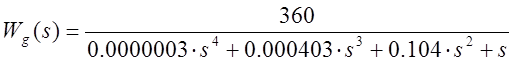Откуда характеристическое уравнение будет выражено как

.

Корни характеристического уравнения разомкнутой системы можно найти с помощью Matlab (рис.2.1)

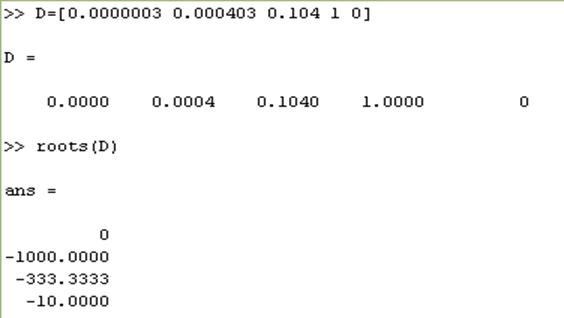
Рис.2.1

Все корни характеристического уравнения расположены в левой полуплоскости.

Построение АФХ можно выполнить с помощью Matlab (рис.2.2):

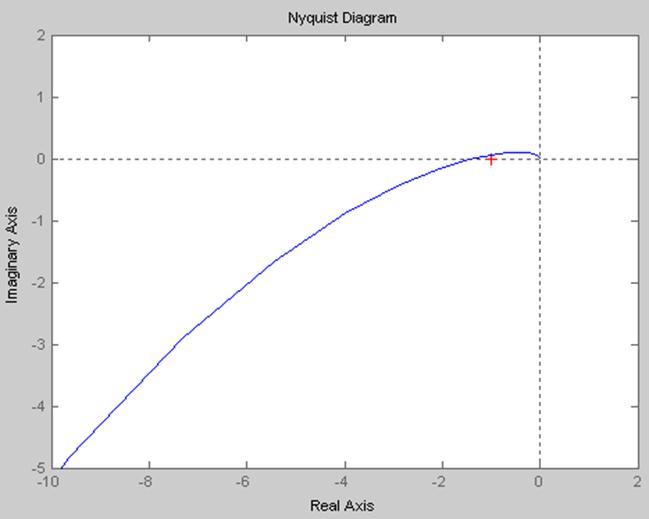
Рис.2.2

Годограф передаточной функции разомкнутой САУ, изображенный на рис.2.2 охватывает точку (–1 ,j0). Что говорит о не устойчивости системы.

2.3.Критерий Михайлова.

Для устойчивости линейной САУ необходимым и достаточным условием является то, что годограф Михайлова при изменении частоты от 0 до +∞, начав движение из точки, лежащей на положительной вещественной полуоси, вращаясь только против часовой стрелки, нигде на обращаясь в нуль, прошел последовательно n-квадрантов и повернулся на угол nπ/2, где   n– степень характеристического полинома.

Передаточная функция замкнутой системы имеет вид

.

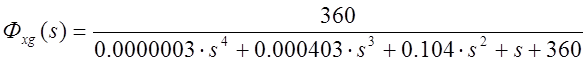Откуда характеристическое уравнение можно записать как

.

С помощью Matlab можно определить корни характеристического уравнения замкнутой системы (рис.2.3)

Рис.2.3

На рис.2.4 изображен годограф Михайлова для замкнутой системы.

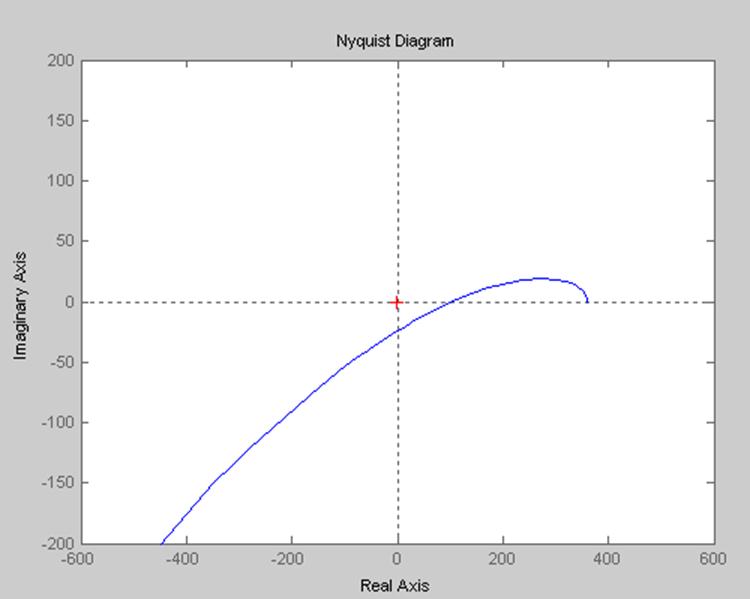
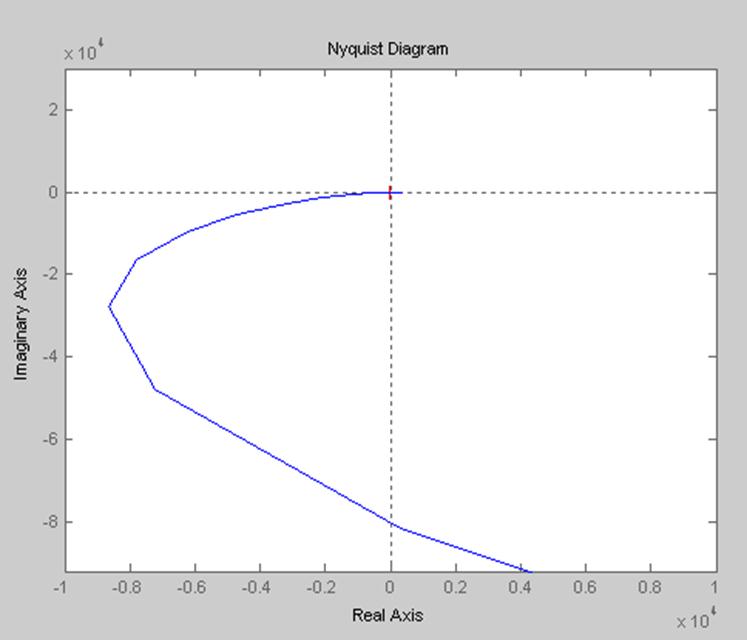
Рис.2.4

Система неустойчива, так как годограф Михайлова, при изменении частоты от 0 до +∞, повернулся по часовой стрелке.

2.4.Анализ логарифмических частотных характеристик.

На рис.2.5 изображены логарифмическая амплитудная характеристика (ЛАХ) и логарифмическая фазная характеристика (ЛЧХ), полученные с помощью Matlab.

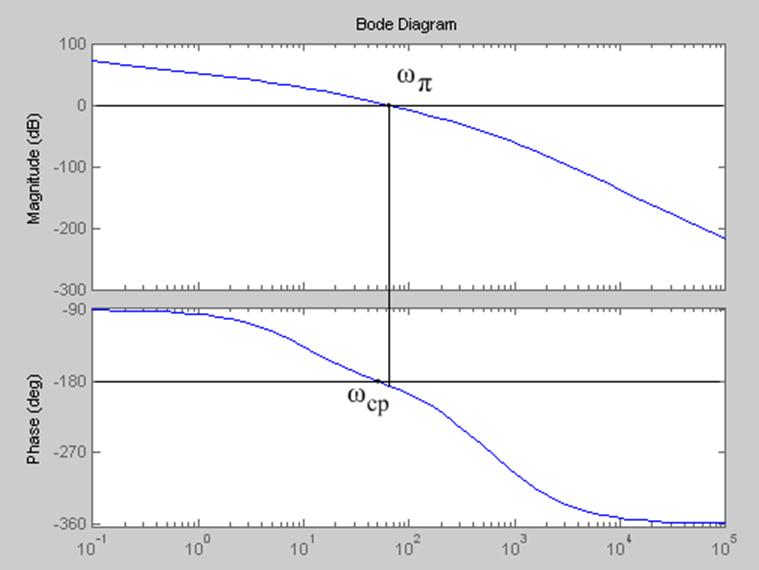
Рис.2.5

По рис.2.5 можно определить ω_π и ω_ср.

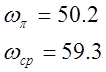
Система неустойчива, так как .

3.Анализ качества нескорректированной САУ.

Переходные характеристики замкнутой системы (рис.1.10) расходятся, что делает невозможным определение времени регулирования и перерегулирование, имеется характерные колебания.

Показатель колебательности μ – это отношение максимального значения мнимой части корней характеристического уравнения к соответствующей вещественной.

С помощью Matlab найдем корни характеристического уравнения замкнутой системы (рис.3.1)

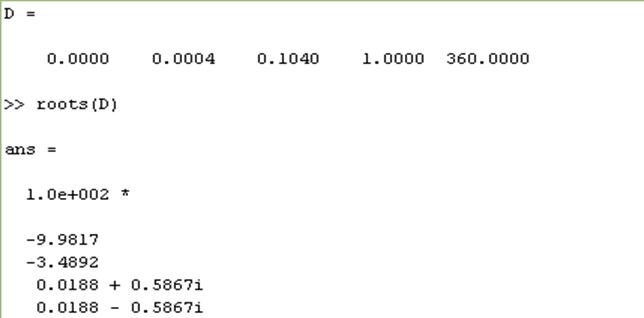
Рис.3.1

Корень с максимальным значением мнимой части:

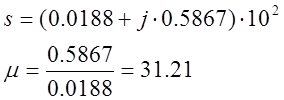
Карта корней характеристического уравнения изображена на рис.3.2

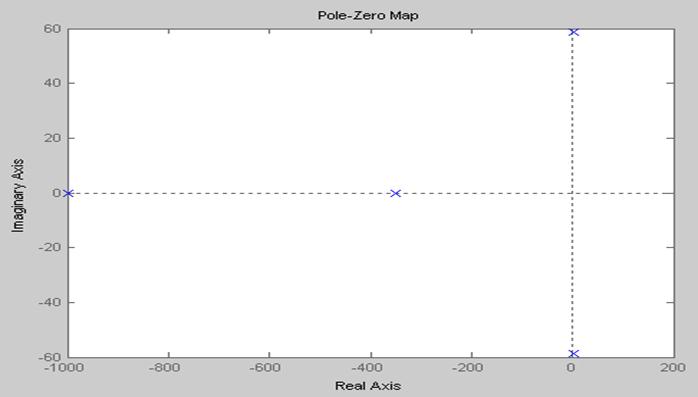
Рис.3.2

Частотные оценки. Запасы устойчивости.

ЛАХ и ЛЧХ нескорректированной САУ (рис.3.3)

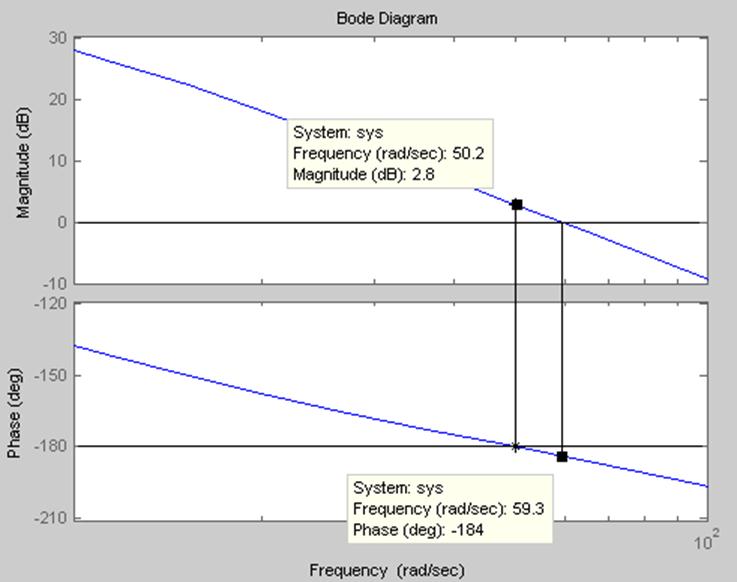
Рис.3.3

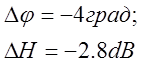
Система имеет отрицательные запасы устойчивости.

4.Синтез корректирующего устройства.

4.1.Синтез корректирующего устройства методом Соколова.

На первом этапе определяется разность порядков полиномов знаменателя (n₁) и числителя (m₁) передаточной функции замкнутой  нескорректированной  системы 

(n₁-m₁).

n₁-m₁=4-0=4

ν=1

На втором этапе формируется желаемая передаточная функция  замкнутой  системы,  удовлетворяющая  заданным требованиям к качеству синтезируемой системы на основе нормированных   передаточных   функций.

Требования к синтезируемой системе:

s^зад=20 %;

=0,25, с

При формировании желаемой передаточной функции

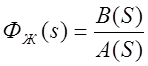степени  m и n соответственно полиномов B(S) и A(S) выбирают,

исходя из следующих соотношений:

m=ν-1=1-1=0,

n=(n₁-m₁)+ν-l=4+1-1=4,                                        

Нормированная передаточная функция Ф_н(р) будет иметь те же порядки n и m. Коэффициенты этой  функции  определяют из  соответствующей   Таблицы А.1 Приложение. Минимальное время регулирования в приложении.

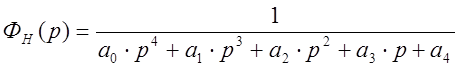
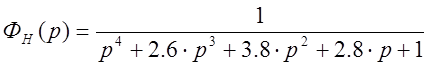
По переходной характеристике нормированной   функции  (рис.4.1) определяют   время переходного процесса τ_н.

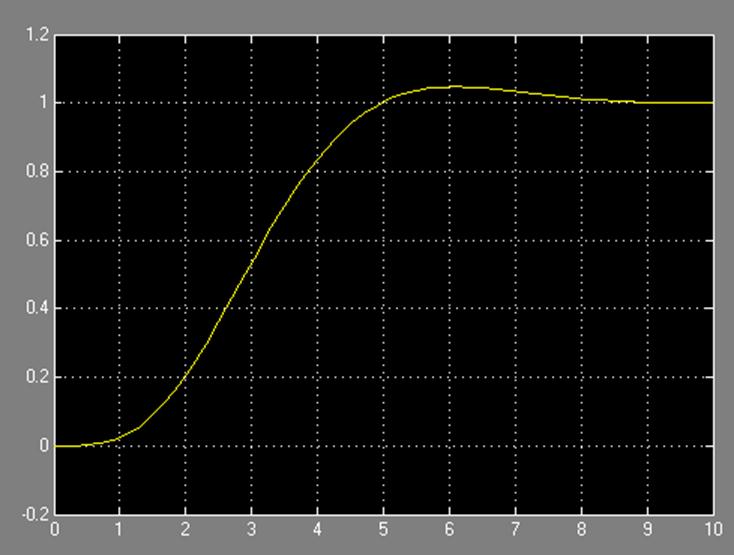
Рис.4.1

τ_н=4.58 c.