Анализ и синтез замкнутой системы автоматического управления, страница 14

Оптимальные настройки для П – регулятора S1_опт = S1(m,w_опт) = 18,421

Рис.65  Кривая равной степени колебательности m=0,221, без запаздывания с И – регулятором и с П – регулятором.

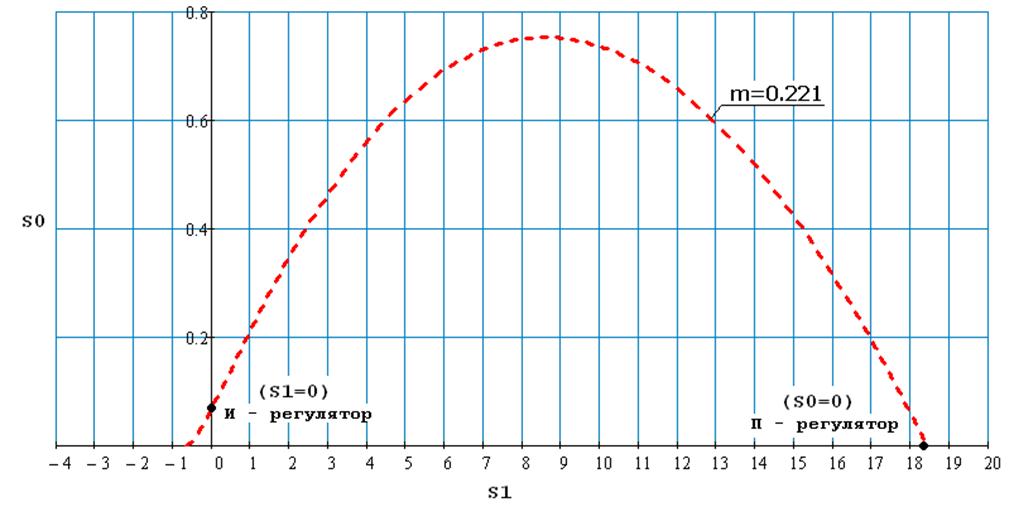
Этап 3. Анализ замкнутой САУ с оптимальными настройками

И - регулятора и П – регулятора

3.1 Построение амплитудно-фазовой характеристики разомкнутой системы и определение запаса устойчивости системы по модулю и по фазе.

Передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора:

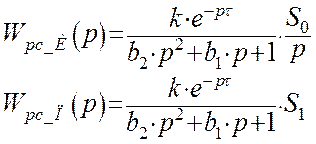
Для построения АФХ разомкнутой системы необходимо знать АФХ используемого регулятора. Поскольку мы рассчитываем систему с И – регулятором и систему с П – регулятором, то сначала рассчитаем их частотные характеристики.

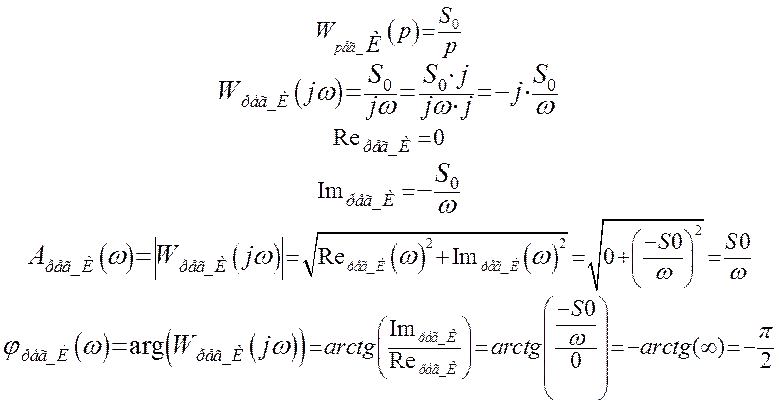
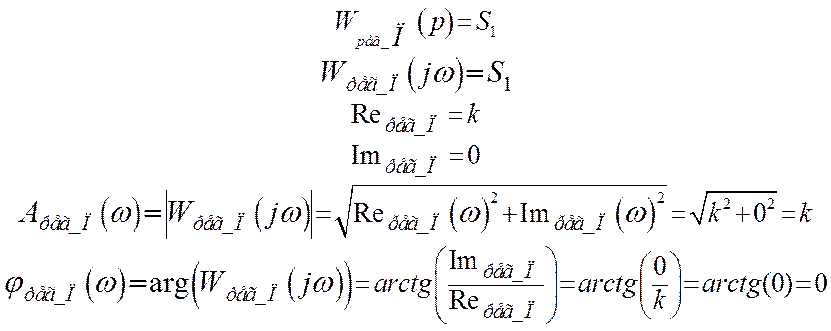
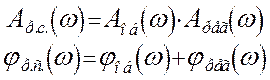
Используя полученные уравнения частотных характеристик, и задаваясь различными значениями w, получим амплитудно-фазовую характеристику разомкнутой системы для каждого регулятора.

Таблица  № 48

	0	0,05	0,1	0,2	0,4	0,5	0,7	1
Ар.с._И()	¥	6,027	1,926	0,434	0,071	0,038	0,014	0,005
р.с._И()	¥	-7,17	-7,73	-2,03	-2,51	-2,62	-2,76	-2,87
Ар.с._П()	2,25	1,746	1,116	0,503	0,165	0,11	0,059	0,029
р.с._П()	-	-2,45	-3,01	-3,6	-4,08	-4,19	-4,33	4,45

Рис.66.  АФХ разомкнутой системы с оптимальными

настройками И–регулятора, с оптимальными

настройками П–регулятора  и t =0

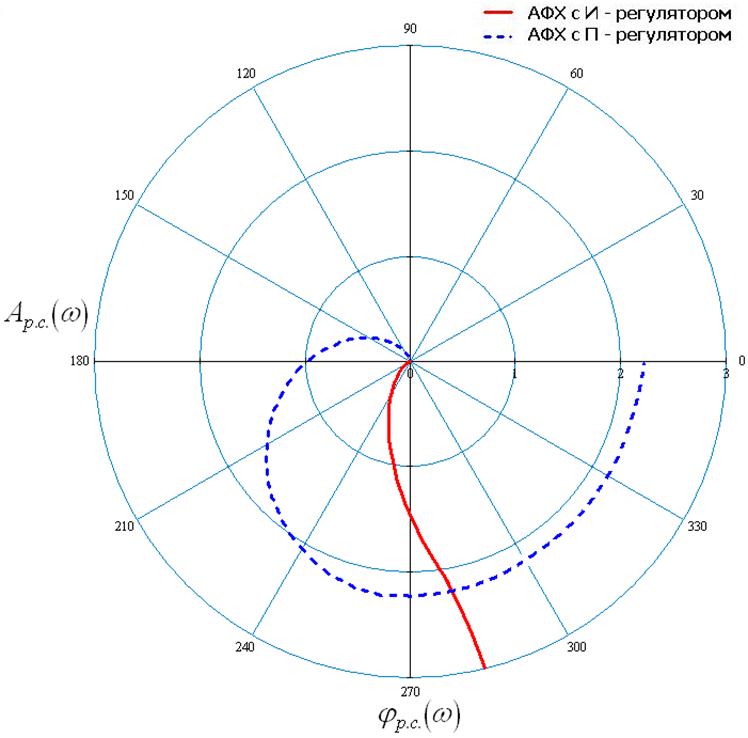
Запас устойчивости по модулю при И и П регуляторах не изменяется. Запас устойчивости по фазе при И – регуляторе увеличивается, а при П – регуляторе уменьшается.

3.2 Расчет переходного процесса в замкнутой системе автоматического регулирования по каналу управления

Построение переходного процесса в замкнутой системе автоматического регулирования без запаздывания по каналу управления для упрощения выполним с помощью следующего интеграла:

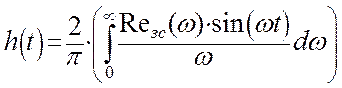
Построим переходные процессы в одних осях для настроек регулятора, взятых в оптимальной точке, правее и левее:

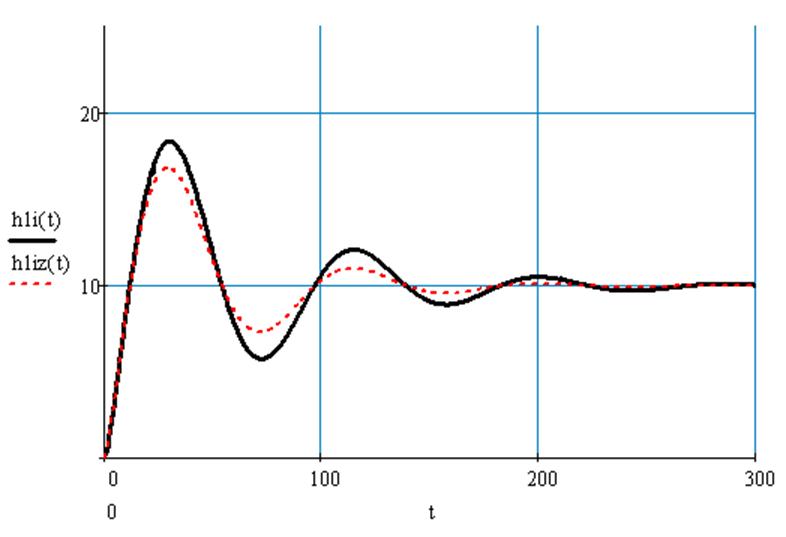
Рис.67 Переходный процесс замкнутой  системы по каналу управления с И – регулятором и переходный процесс замкнутой  системы по каналу управления с П – регулятором при оптимальных настройках и  t=0

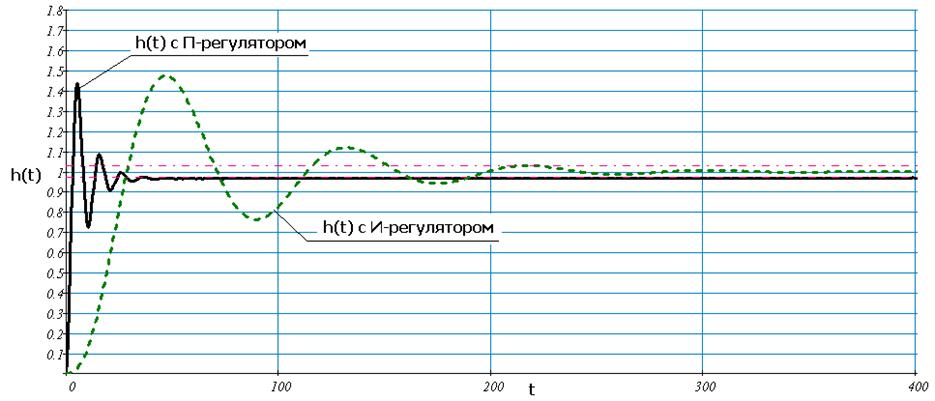
По полученному графику определим показатели качества для переходного процесса без запаздывания и с оптимальными настройками И – регулятора и П – регулятора.

Время переходного процесса  для И – регулятора T = 240с

Величина перерегулирования  для И – регулятора σ = 47,7%

Время переходного процесса  для П – регулятора T = 60с

Величина перерегулирования  для П – регулятора σ = 44,5%

При анализе переходного процесса по каналу управления с И – регулятором на возможное появление статической ошибки установлено следующее:

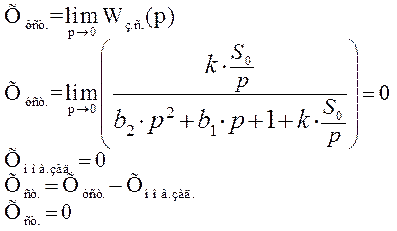
Квадратичная интегральная оценка с И – регулятором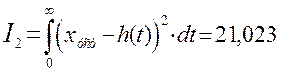

При анализе переходного процесса по каналу управления с П – регулятором на возможное появление статической ошибки установлено следующее:

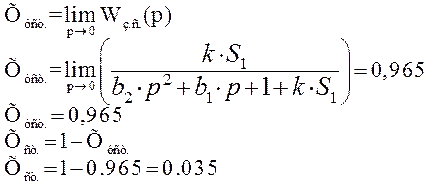
Квадратичная интегральная оценка с П – регулятором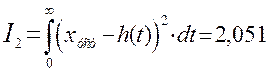

По графику переходных процессов каналу управления сделаем следующее заключение.

П - регулятор обладает высоким быстродействием, время регулирования достаточно маленькое. Однако так же обладает статической ошибкой, уменьшить её можно, но это выведет систему на границу устойчивости. И – регулятору для создания воздействия необходимо больше времени, чем П – регулятору, т.е. он работает медленно. Но статическая ошибка равна нулю.

3.3 Расчет переходного процесса в замкнутой системе автоматического регулирования по каналам возмущения

Для построения переходного процесса в замкнутой системе по первому каналу возмущения с И – регулятором и с П – регулятором предварительно выведем передаточную функцию:

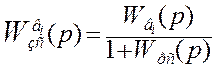
Представим в показательной форме:

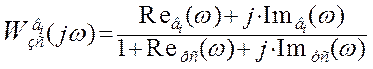
Построение переходного процесса в замкнутой системе автоматического регулирования по каналу возмущения выполним по интегралу:

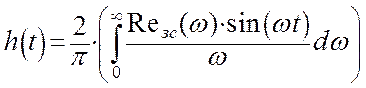
где R_зс(w) - вещественная частотная характеристика замкнутой системы, которая представлена в общем виде:

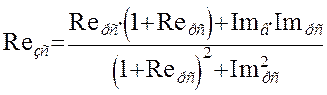
Приведем передаточную функцию  к отношению произведений полиномов, подставив в формулу  полученные ранее выражения передаточных функций: объекта по каналам управления, возмущения, и регулирования.

Передаточная функция замкнутой системы по первому каналу возмущения с И – регулятором примет следующий вид:

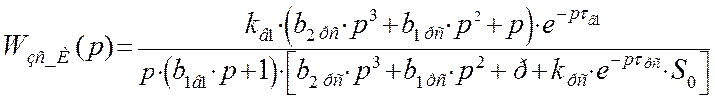
Найдем изображение переходной функции замкнутой системы:

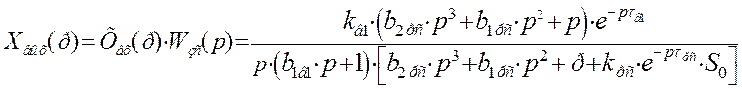
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения с И - регулятором:

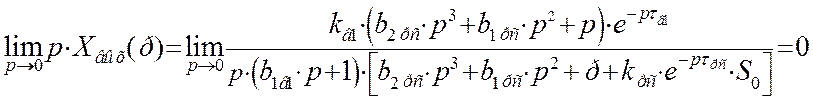
                       При анализе переходного процесса по первому каналу возмущения на возможное появление статической ошибки установлено следующее:

Квадратичная интегральная оценка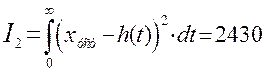

Рис.68  Переходный процесс по первому каналу возмущения в системе с И – регулятором без запаздывания и с запаздыванием.

Передаточная функция замкнутой системы по первому каналу возмущения с П – регулятором примет следующий вид:

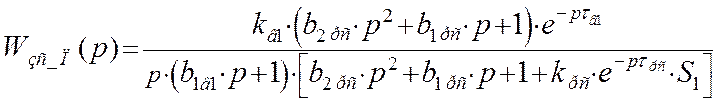
Найдем изображение переходной функции замкнутой системы:

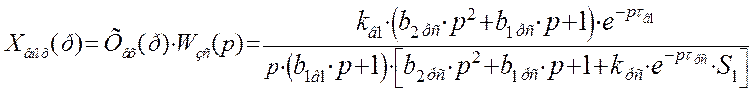
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения с П - регулятором:

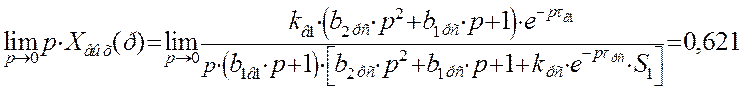
При анализе переходного процесса по первому каналу возмущения на возможное появление статической ошибки установлено следующее:

Квадратичная интегральная оценка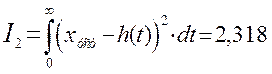

Рис.69  Переходный процесс по первому каналу возмущения в системе с П  регулятором без запаздывания и с запаздыванием.

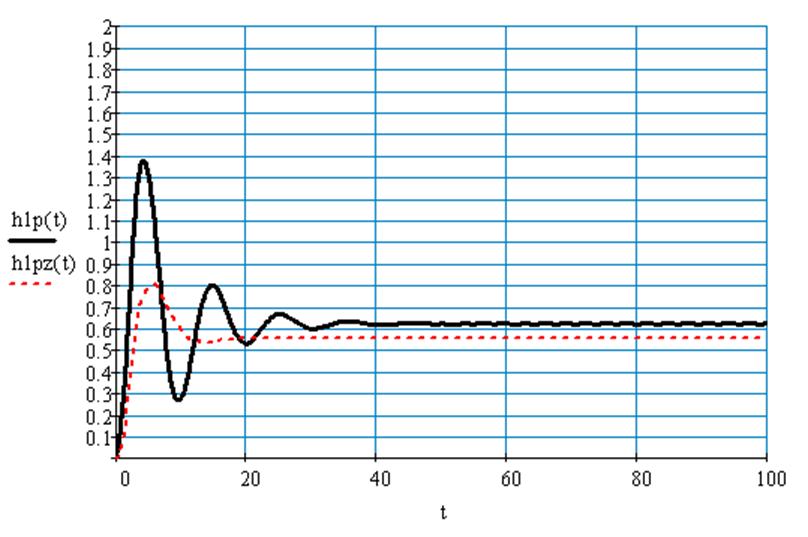
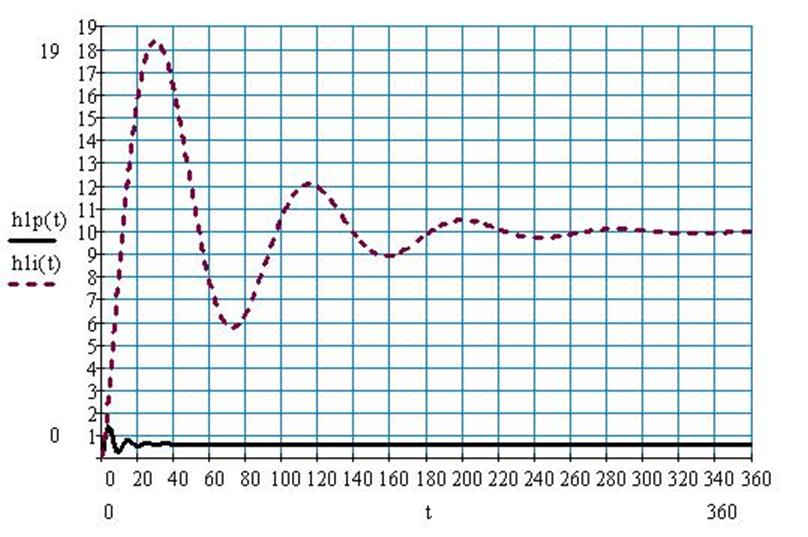
Рис.70  Переходный процесс по первому каналу возмущения в системе с И  регулятором и в системе с П  регулятором без запаздывания.

Для построения переходного процесса в замкнутой системе по второму каналу возмущения с И – регулятором и с П – регулятором предварительно выведем передаточную функцию:

Передаточная функция замкнутой системы по второму каналу возмущения с И – регулятором примет следующий вид:

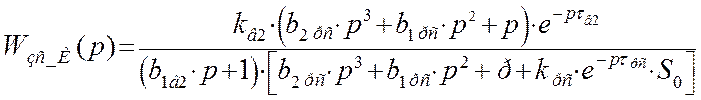
Найдем изображение переходной функции замкнутой системы: