Анализ и синтез замкнутой системы автоматического управления, страница 2

w	0	0,01	0,02	0,03	0,05	0,07	0,1	0,115	0,116	0,12	0,14	0,18	0,2
j(w)	0	-0,219	-0,431	-0,632	-0,988	-1,286	-1,642	-1,797	-5,154	-5,07	-4,69	-4,107	-3,878

Рис3 Фазо-частотная характеристика по каналу регулирования

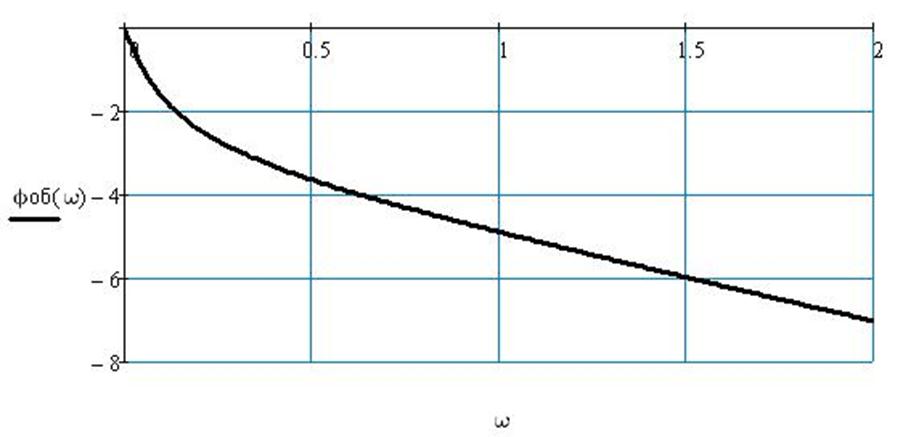
Так как объект по каналу регулирования является комбинацией колебательного звена  и звена транспортного запаздывания, то в режиме гармонических колебаний он вносит отрицательны фазовые сдвиги.

- построение амплитудно-фазовой характеристики

Определяем вещественную и мнимую части.

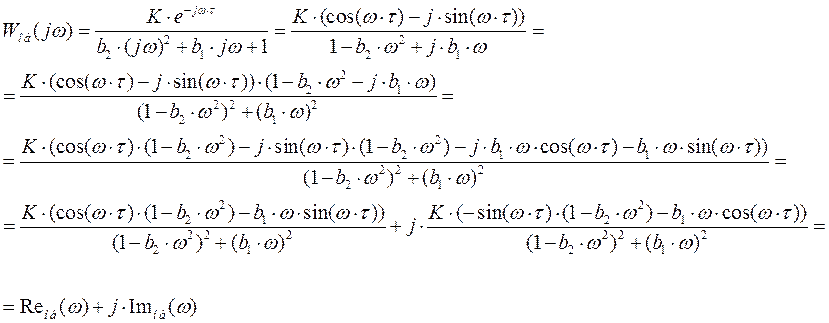
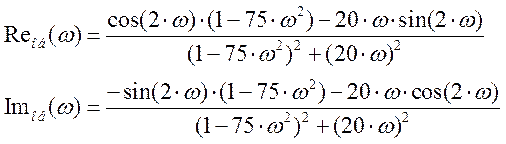
Расчетные данные для построения АФХ в Таблице 4

Таблица 4

w	0	0,02	0,04	0,06	0,08	0,1	0,12	0,14	0,18	0,2	0,3
Reоб(w)	1,5	1,299	0,862	0,442	0,137	-0,056	-0,169	-0,228	-0,261	-0,255	-0,177
Imоб(w)	0	-0,597	-0,92	-0,972	-0,881	-0,742	-0,601	-0,477	-0,286	-0,218	-0,037

w	0,4	0,5	0,6	0,7	0,7869	0,787	0,7875	0,788
Reоб(w)	-0,109	-0,065	-0,038	-0,02	-0,01	-0,01	-0,01	-0,01
Imоб(w)	0,019	0,034	0,036	0,03	0,03	0,03	0,029	0,029

Рис.4  Амплитудно-фазовая  характеристика по каналу регулирования

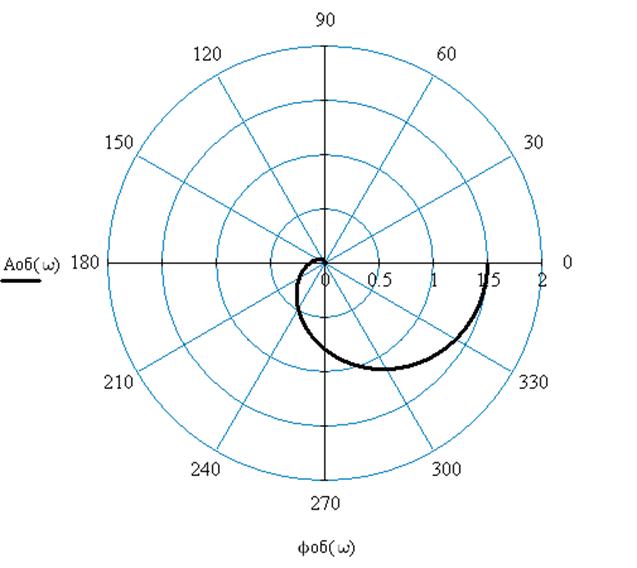
1.2. Первый канал возмущения

- построение переходной функции

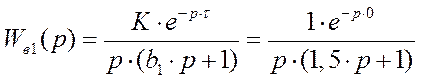
Так как запаздывание только сдвигает переходную функцию на время t, то вывод переходной функции будем делать для аналогичного звена без запаздывания, т.к. t=0 вэ том случай переходная функция будет выглядеть, так же как и переходная функция реального интегрирующего звена.

Таким образом, передаточную функцию объекта представим в  виде:

W_в1(p)=W_в1⁰(p)×е^-pt

Х_вх(t)=1(t) – входной сигнал.

Изображение выходного сигнала имеет вид:

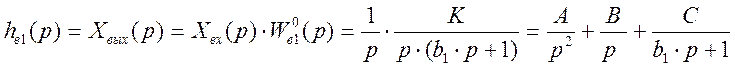
Определяем коэффициенты А, В, С:

A×(b₁×p + 1) + B×p×(b₁×p + 1) + С×р² =A×b₁×p + A + B×b₁× p² + B×p + C×p² = K

при р²: B×b₁+C = 0

при р¹: A×b₁ + B = 0

при р⁰: A = K

A =K

B = -K× b₁

C = K× b₁²

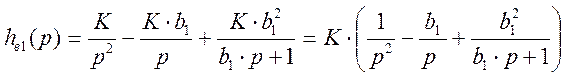
Находим оригинал:

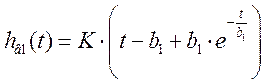
Учтем явление транспортного запаздывания, то есть при t ³ t переходная функция имеет вид:

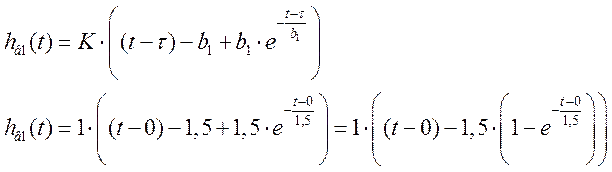
При  t < t   h(t) = 0.

Расчетные данные для построения переходного процесса в Таблице 5

Таблица 5

t	0	1	2	4	6	8	10	12	16	18	20
h(t)	0	0,568	1,509	3,5	5,5	7,5	9,5	11,5	15,5	17,5	19,5

Рис.5 Переходная функция объекта по каналу возмущения 1.

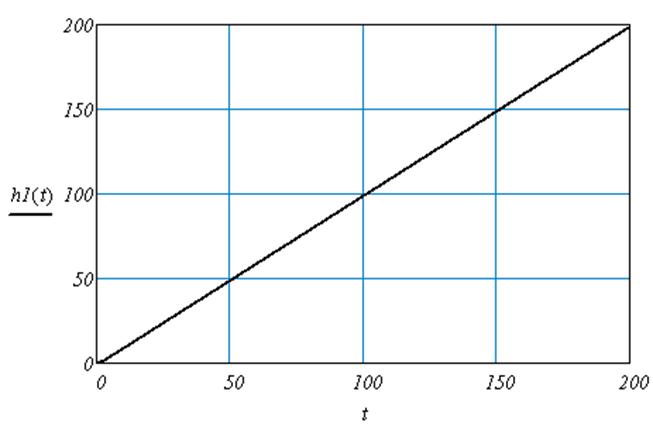
Так как передаточная функция объекта по каналу регулирования представляет собой передаточную функцию реального интегрирующего звена, то переходный процесс объекта по каналу регулирования имеет астатический характер и по окончании переходного процесса выходная величина изменяется по линейному закону. Передаточная функция включает в себя и передаточную функцию звена запаздывания, но время запаздывания t = 0, поэтому переходный процесс сдвигаться не будет.

- построение амплитудно-частотной характеристики

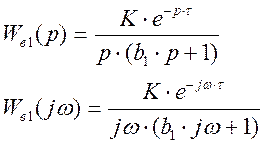
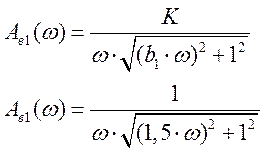
Расчетные данные для построения АЧХ в Таблице 6

Таблица 6

w	0	0,1	0,3	0,5	0,7	1	1,5	2	3	4	6	10	14
А(w)	¥	9,9	3,29	1,94	1,34	0,89	0,53	0,35	0,18	0,11	0,05	0,02	0,01

Рис. 6  Амплитудно-частотная характеристика  по каналу возмущения 1.

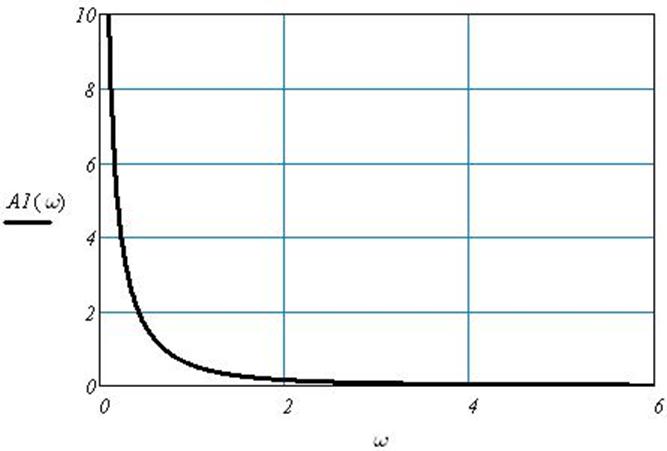
Объект по каналу возмущения 1 является фильтром низких частот потому, что по этому каналу объект является интегрирующим звеном.

- построение фазо-частотной характеристики

    

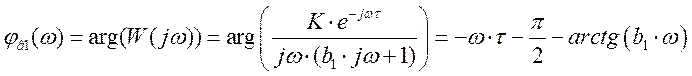
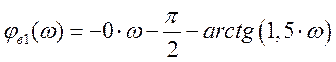
Расчетные данные для построения ФЧХ в Таблице 7

Таблица 7

w	0	0,2	0,4	0,6	0,8	1	1,4	1,6	2
j(w)	-1,57	-1,67	-1,767	-1,861	-1,951	-2,034	-2,181	-2,245	-2,355

Рис. 7 Фазо-частотная характеристика  по каналу возмущения 1.

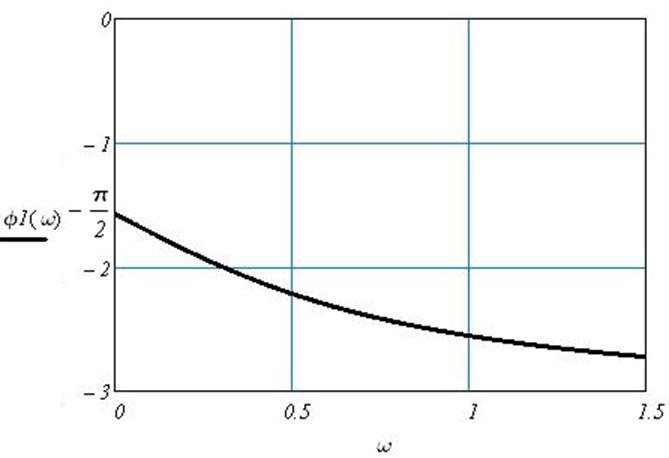
Так как объект по каналу возмущения 1 является комбинацией реального интегрирующего звена и звена транспортного запаздывания, то в режиме гармонических колебаний  он вносит отрицательные фазовые сдвиги.

- построение амплитудно-фазовой характеристики

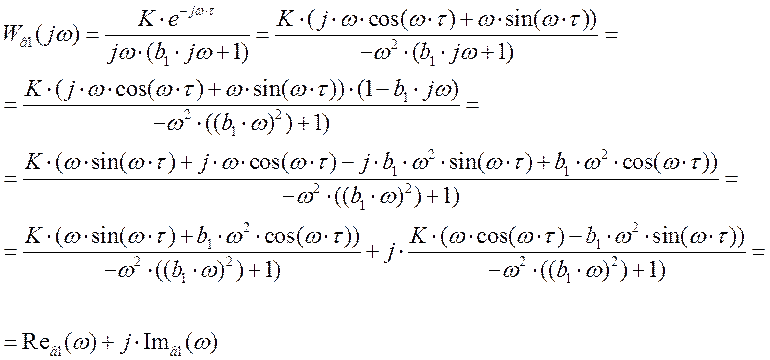
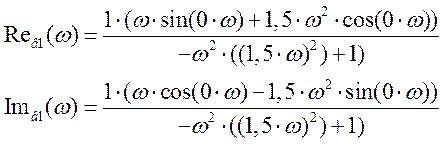
Расчетные данные для построения АФХ в Таблице 8

Таблица 8

w	0	0,05	0,1	0,15	0,2	0,3	0,4	0,5	0,7	0,9	1,2
Re(w)	¥	-0,48	-0,48	-0,48	-0,47	-0,44	-0,41	-0,38	-0,32	-0,27	-0,20
Im(w)	¥	-19,9	-9,87	-6,48	-4,76	-3,06	-2,12	-1,55	-0,93	-0,63	-0,34

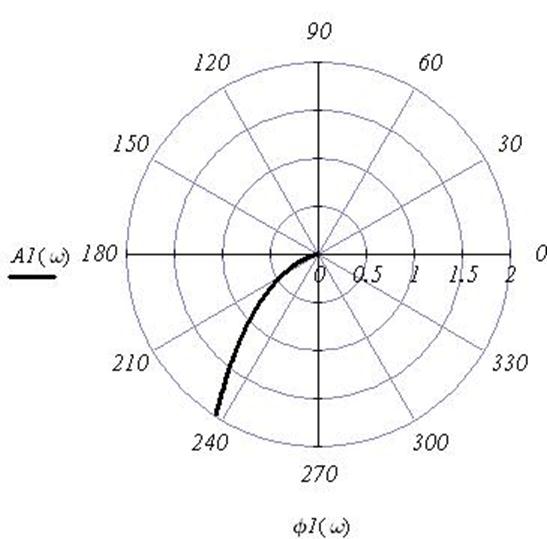
Рис.8  Амплитудно-фазовая  характеристика по каналу возмущения 1

1.3. Второй канал возмущения

- построение переходной функции

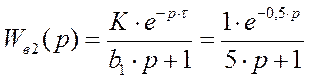
Так как запаздывание только сдвигает переходную функцию на время t, то вывод переходной функции будем делать для апериодического звена 1-го порядка без запаздывания, а «t» - учтем в окончательной формуле. Таким образом, передаточная функция объекта имеет вид:

W_в2(p)=W_в2⁰(p)×е^-pt

Х_вх(t)=1(t) – входной сигнал.

Изображение выходного сигнала имеет вид:

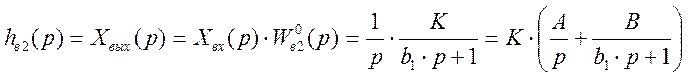
Определяем коэффициенты А, В: