Анализ и синтез замкнутой системы автоматического управления, страница 10

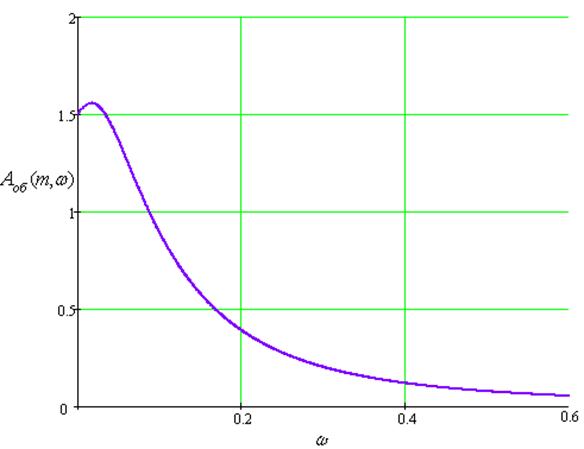
Расширенная фазо-частотная характеристика объекта по каналу регулирования

Выражение для расширенной фазо-частотной характеристики найдем как разность аргументов числителя и знаменателя:

 

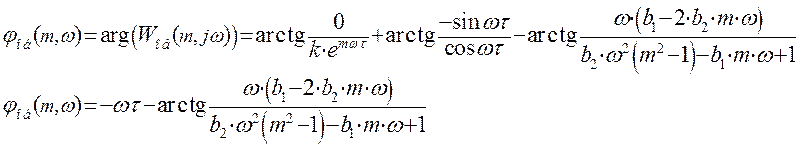
Функция 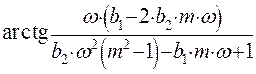 имеет две точки разрыва, в которых функция arctg изменяется с p/2 до -p/2, однако нас интересует поведение функции при положительном значении частоты ω. Чтобы найти эти точки, необходимо приравнять знаменатель функции к нулю.

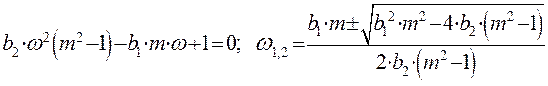
Для обеспечения непрерывности графика РАФХ необходимо прибавить период, равный -p:

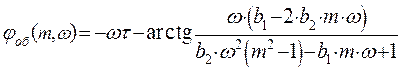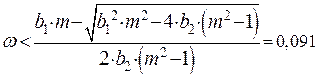
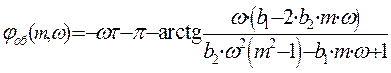 при

 при

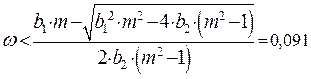
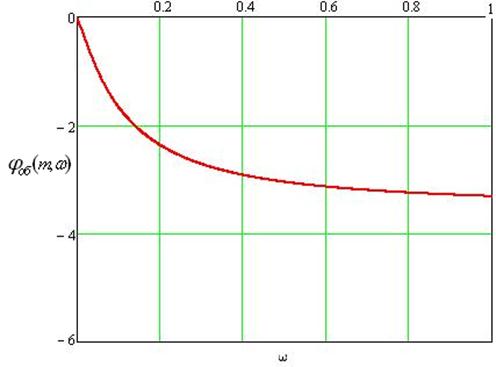
Расчетные данные для построения РФЧХ в Таблице 43. Расширенная ФЧХ проходит ниже обыкновенной ФЧХ.

Таблица 43

w	0	0,005	0,01	0,03	0,07	0,1	0,3	0,7	1	3
j(m,w)	0	-0,101	-0,204	-0,617	-1,302	-2,083	-2,721	-3,202	-3,316	-3,491

Рис.45 Расширенная фазо-частотная характеристика по каналу регулирования со степенью колебательности m=0,221 и без запаздывания.

2.2.   Построение кривой равной степени колебательности m=0,221 для объекта без запаздывания и выбор оптимальных, левых и правых настроечных параметров регулятора.

Для реализации задачи синтеза САУ необходимо в плоскости настроек ПИ – регулятора построить кривую равной степени колебательности и на ней выбрать точку, соответствующую минимуму квадратичной интегральной оценки качества. Эта точка обычно находится при w_опт = 1.3 ^. w_max , где w_max – значение частоты w  в максимуме графика S₀(S₁).

Чтобы заданная система имела переходный процесс с заданной степенью колебательности m нужно, чтобы РАФХ заданной системы проходила через точку с координатами (-1, j^·0), т.е.:

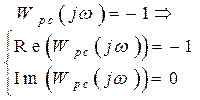
При этом степень колебательности будет равна m. Из этих условий найдем настройки пропорционально-интегрального регулятора. Для этого в передаточной функции регулятора сделаем  подстановку: p=-m·w+j·w,:

 

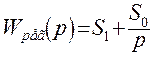
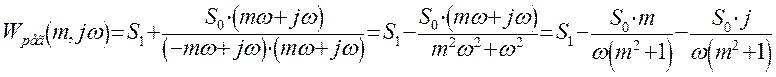
Представим передаточную функцию объекта в показательном виде:

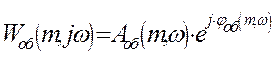
Используя уравнение Эйлера, получим:

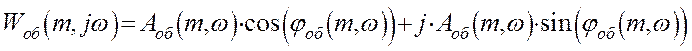
Поскольку передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора , следовательно, передаточную функцию разомкнутой системы можно также представить в показательном виде. В свою очередь, условия устойчивости  по критерию Найквиста представим в показательной форме, то есть мы можем составить систему из двух уравнений:

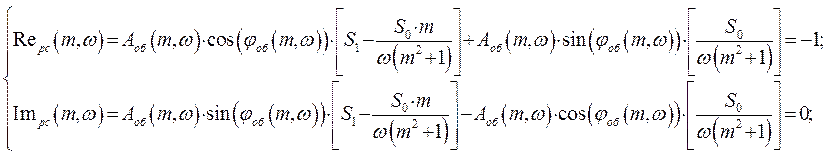
Можно получить область, где находятся значения настроечных параметров S₀, S₁, w.

Решая систему уравнений, найдем настройки пропорционально-интегрального регулятора

Решение этой системы для S₀, S₁ :

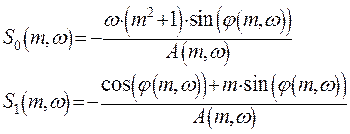
Используя полученные уравнения настроек регулятора, и задавая различные значениям w, получим кривую заданной степени колебательности m=0,221:

Расчетные данные для построения кривой равной степени колебательности в Таблице 44

Таблица 44

						w max		w лев	w опт	w прав
w	0	0,03	0,05	0,1	0,2	0,39829	0,45	0,48438	0,51777	0,54937	0,55	0,6
S1	-0,667	-0,451	-0,265	0,349	2,219	8,45	10,627	12,2	13,825	15,45	15,484	18,232
S0	0	0,012	0,032	0,117	0,374	0,754	0,72	0,647	0,532	0,377	0,374	0,028

Рис.46  Кривая равной степени колебательности m=0,221 и без запаздывания

Так как объект по каналу регулирования является статическим, то кривая равной степени колебательности выходит из отрицательной области настройки S₁.

Оптимальные настройки ПИ-регулятора, обеспечивающие при заданной степени колебательности  минимизацию квадратичной интегральной оценки переходного процесса в замкнутой системе, определяются как координаты точки, лежащей на правой ветви кривой S0-S1 вблизи ее вершины. Найти положение этой точки без расчета квадратичной интегральной оценки можно, используя  знания о том, что в точке с оптимальными настройками значение частоты составляет примерно  на (20—30)%   больше   частоты в точке максимума кривой S0-S1.

 Согласно графику:

  w_max = 0,39829   =>    w_опт = 1.3w_max = 1.3·0,39829 = 0,51777

Находим  оптимальные  настройки ПИ-регулятора:

S0_опт = S0(m,w_опт) = 0,532

     S1_опт = S1(m,w_опт) = 13,825

w _лев = 0,0,48438

S0_лев = S0(m,w_лев) = 0,647

S1_лев = S1(m,w_лев) = 12,2

w _прав = 0,54937

S0_прав = S0(m,w_прав) = 0,377

S1_прав = S1(m,w_прав) = 15,45

Этап 3. Анализ замкнутой САУ с тремя парами настройками регулятора.

3.1 Построение амплитудно-фазовой характеристики разомкнутой системы и определение запаса устойчивости системы по модулю и по фазе

Передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора:

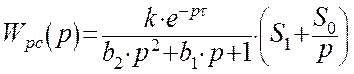
Для построения АФХ разомкнутой системы необходимо знать АФХ используемого регулятора. Поскольку мы рассчитываем систему с ПИ – регулятором, то сначала рассчитаем его частотные характеристики.

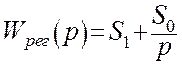
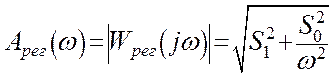
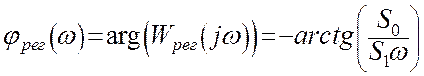
Для получения вещественной и мнимой частотных характеристик разомкнутой системы надо числитель и знаменатель выражения частотной передаточной функции помножить на число, сопряженное со знаменателем и упростить полученное выражение. Как было найдено ранее вещественная и мнимая характеристики разомкнутой системы при учете τ=0 выражаются:

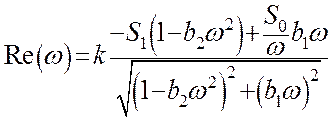
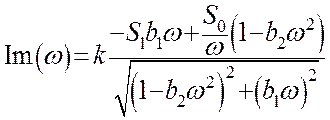
Используя полученные уравнения вещественной и мнимой частотных характеристик, и задаваясь различными значениями w, получим амплитудно-фазовую характеристику разомкнутой системы. Определим запас устойчивости по модулю и фазе.

Рис.47.  АФХ разомкнутой системы с оптимальными настройками иt =0

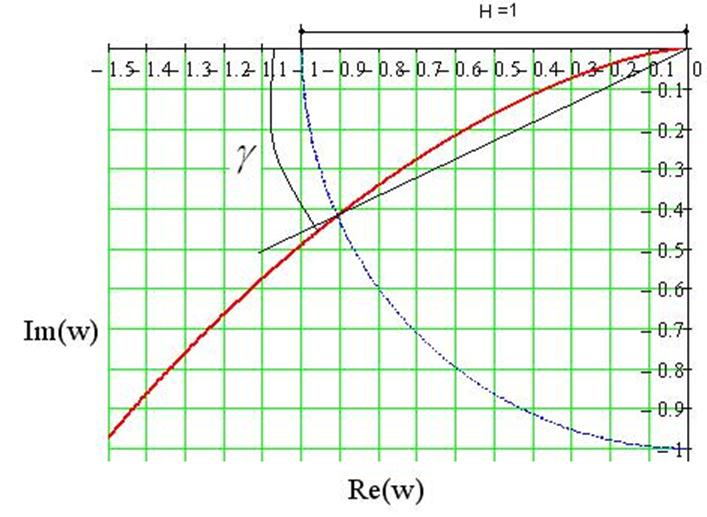
При оптимальных настройках: H=1, g =24°74'

Для нахождения амплитудно-фазовой характеристики разомкнутой системы для левых настроек ПИ-регулятора выполним последовательность вычислений, аналогично приведенным выше.

Рис.48.  АФХ разомкнутой системы с настройками, расположенными левее оптимальных, и t =0

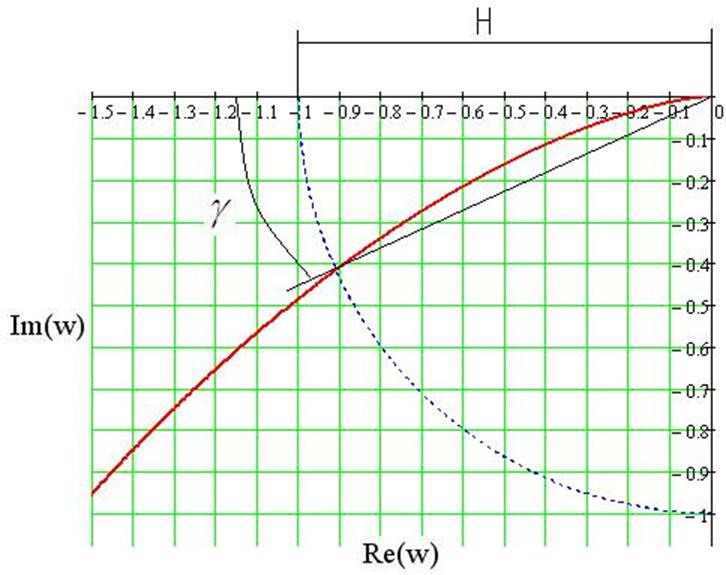
При настройках левее оптимальных: H=1, g =24°53'