Анализ и синтез замкнутой системы автоматического управления, страница 5

Расчетные данные для построения кривой равной степени колебательности в Таблице 19

Таблица 19

w	0	0,001	0,01	0,05	0,1	0,15	0,2	0,23517	0,25	0,27
S1	-0,667	-0,66	-0,595	-0,19	0,535	1,417	2,363	3,016	3,279	3,451
S0	0	0,0000153	0,0015	0,033	0,107	0,175	0,179	0,112	0,06	0,016

Рис.19  Кривая равной степени колебательности

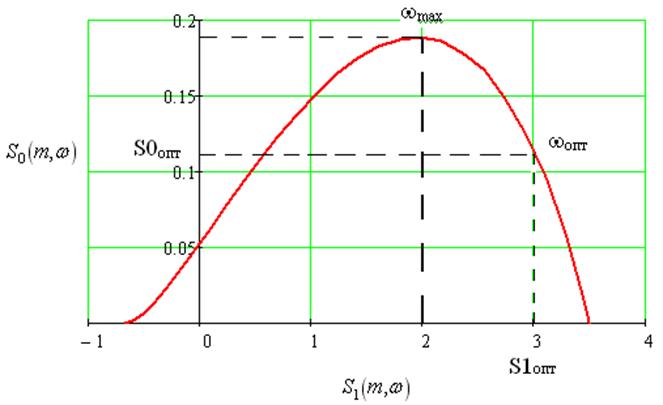
Так как объект по каналу регулирования является статическим, то кривая равной степени колебательности выходит из отрицательной области настройки S₁.

2.3 Определение оптимальных настроек ПИ-регулятора

Оптимальные настройки ПИ-регулятора, обеспечивающие при заданной степени колебательности  минимизацию квадратичной интегральной оценки переходного процесса в замкнутой системе, определяются как координаты точки, лежащей на правой ветви кривой S0-S1 вблизи ее вершины. Найти положение этой точки без расчета квадратичной интегральной оценки можно, используя  знания о том , что в точке с оптимальными настройками значение частоты составляет примерно  на (20—30)%   больше   частоты в точке максимума кривой S0-S1.

 Согласно графику

  w_max = 0,1809   =>    w_опт = 1.3w_max = 1.3·0.1809 = 0,23517

Находим  оптимальные  настройки ПИ-регулятора:

         S0_опт = S0(m,w_опт) = 0,112

         S1_опт = S1(m,w_опт) = 3,016

Этап 3. Анализ замкнутой САУ с оптимальными настройками

ПИ-регулятора

3.1. Построение АФХ разомкнутой системы

АФХ разомкнутой системы имеют вид:  

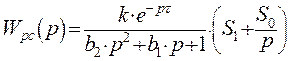
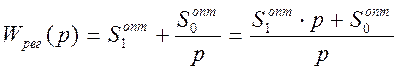
Из выражения следует, что для построения АФХ разомкнутой системы необходимо знать АФХ используемого регулятора. Поскольку мы рассчитываем систему с ПИ – регулятором, то сначала рассчитаем его частотные характеристики:

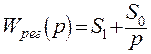
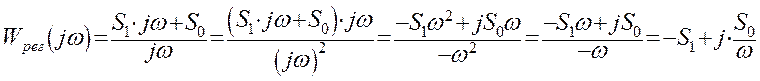
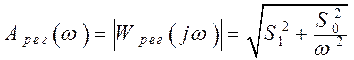
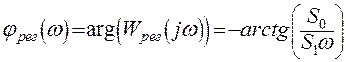
Для получения вещественной и мнимой частотных характеристик разомкнутой системы надо числитель и знаменатель выражения частотной передаточной функции  помножить на число, сопряженное со знаменателем и упростить полученное выражение:

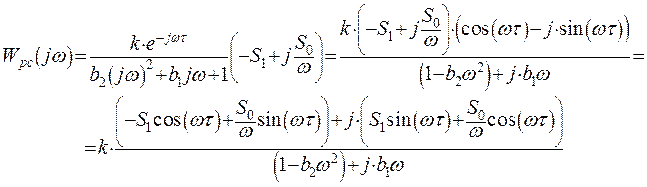
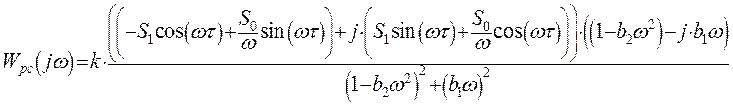
Представим результат преобразований в виде вещественной и мнимой частотных характеристик:

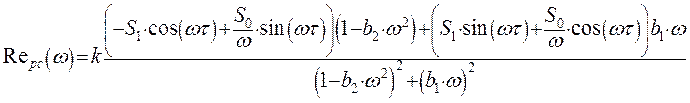
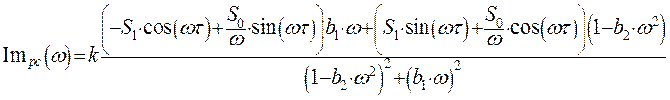
Используя полученные уравнения вещественной и мнимой частотных характеристик, и задаваясь различными значениями w, получим амплитудно-фазовую характеристику разомкнутой системы.

Расчетные данные для построения АФХ разомкнутой системы в Таблице 20

Таблица 20

w	0,01	0,02	0,03	0,04	0,05	0,1	0,15	0,2	0,5
Reрс(w)	0,759	0,572	0,31	0,024	-0,247	-1,001	-1,052	-0,891	-0,188
Imрс(w)	-17,168	-9,075	-6,484	-5,19	-4,367	-2,175	-1,089	-0,514	-0,118

Рис.20  Амплитудно-фазовая характеристика разомкнутой системы

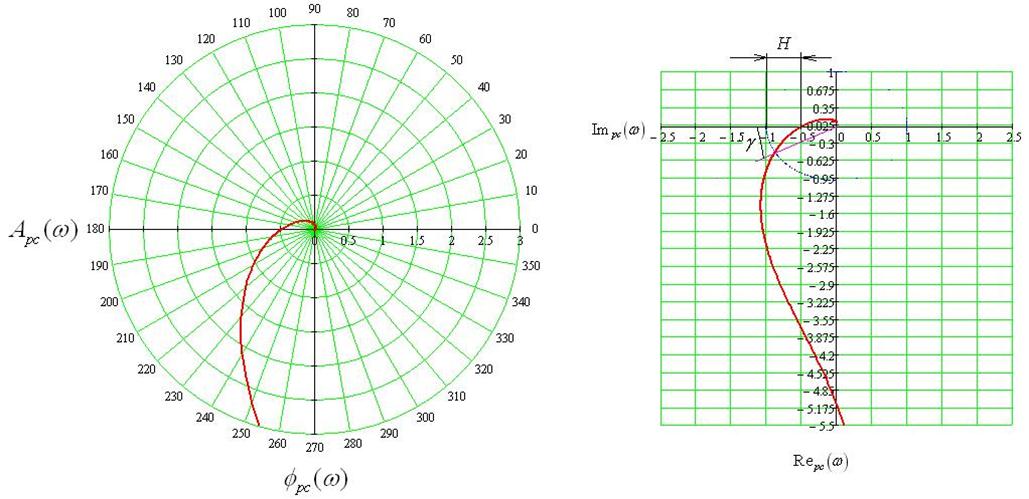
Замкнутая система является устойчивой, так как АФХ разомкнутой системы не охватывает точку (-1,j×0).

3.2. Определение запаса устойчивости

Определим запас устойчивости по модулю и фазе. Запас устойчивости по модулю определяется как расстояние от годографа амплитудно-фазовой характеристики разомкнутой системы до точки с координатами (-1;j·0). Запас устойчивости по фазе определяется как угол между отрицательным направлением оси вещественной частотной характеристики Re(w) и единичного вектора A(w) разомкнутой системы.

- определение запаса устойчивости по фазе.

Определяем из графика значение мнимой части АФХ при w=w_ср , то есть при A_рс(w)=1:

Im(w_ср)=0,437

- определение запаса устойчивости по модулю.

Определяем из графика значение амплитуды, при которой j(w)=-p :

Определяем запас устойчивости по модулю:

В ТАУ считается, что система обладает хорошим запасом устойчивости, если  и

3.3. Построение переходного процесса в замкнутой системе по каналу управления

Расчет переходного процесса в замкнутой системе при наличии запаздывания в канале регулирования ведется методом вещественных частотных характеристик – методом трапеций. Это графоаналитический метод.

Сначала нужно построить график вещественной частотной характеристики замкнутой системы. Эта функция представляет собой вещественную часть передаточной функции замкнутой системы по анализируемому каналу.

Для построения переходного процесса используем метод трапеций.

Вывод  передаточной  функции  замкнутой  системы  по  каналу  управления:

Передаточную функцию замкнутой системы регулирования можно представить как передаточную функцию разомкнутой системы охваченной отрицательной обратной связью.

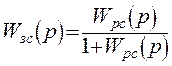
Выведем аналитическое выражение для расчета вещественной части частотной характеристики замкнутой системы Re_зс(w) через определенные ранее частотные характеристики разомкнутой системы. Обозначим Re_рс(w) – вещественную частотную характеристику разомкнутой системы, а Im_рс(w) – мнимую частотную характеристику разомкнутой системы и подставим их в выражение:

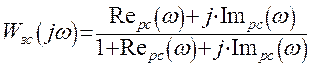
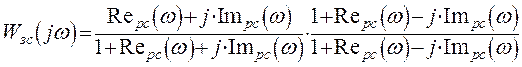
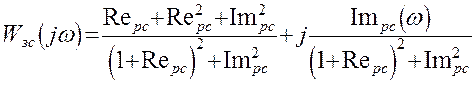
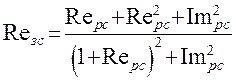
Используя полученное уравнение вещественной частотной характеристики замкнутой системы  и задаваясь различными значениями w, получим кривую вещественной частотной характеристики.

Расчетные данные для построения переходного процесса в замкнутой системе по каналу регулирования  в Таблице 21

Таблица 21

w	0	0,005	0,01	0,05	0,1	0,15	0,2	0,25	0,28	0,3	0,4	0,5	0,8
Reзс(w)	1	0,998	0,994	0,962	1	1,044	0,606	-1,259	-1,389	-1,183	-0,452	-0,207	-0,015

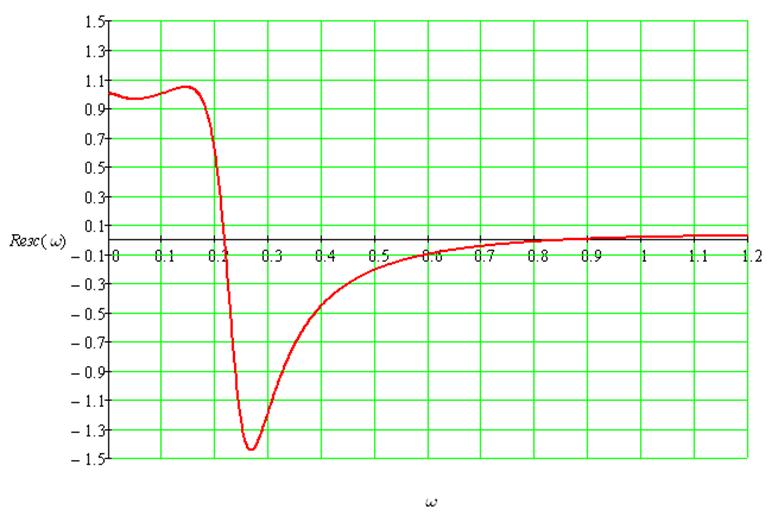
Рис.21 Вещественная частотная характеристика

 замкнутой системы по каналу управления (задание – выход)