Анализ и синтез замкнутой системы автоматического управления, страница 4

w	0	0,01	0,03	0,06	0,07	0,1	0,15	0,2	0,25	0,3	0,4	0,5
j(w)	0	-0,322	-0,984	-1,805	-1,989	-2,36	-2,708	-2,953	-3,174	-3,391	-3,834	-4,291

Рис.15 Фазо-частотная характеристика по каналу возмущения 3

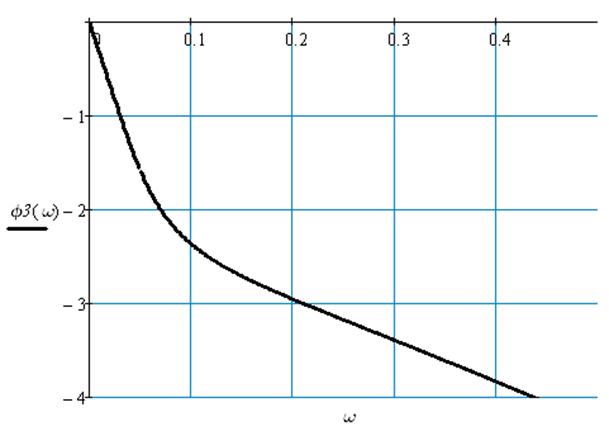
В режиме гармонических колебаний  присутствуют отрицательные фазовые сдвиги из-за составляющей колебательного звена и звена транспортного запаздывания. А так как еще есть и составляющая пропорционально-дифференциального звена, то могут быть  положительные фазовые сдвиги, но они не проявились из-за того, что коэффициенты пропорционально-дифференциального звена небольшие, т.е. его влияние слабее влияния колебательного звена и звена транспортного запаздывания.

- построение амплитудно-фазовой характеристики

Для получения амплитудно-фазовой характеристики необходимо найти вещественную и мнимую частотные характеристики.

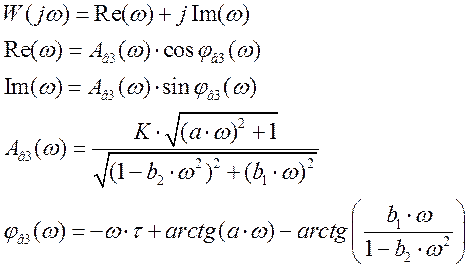
Расчетные данные для построения АФХ в Таблице 16

Таблица 16

w	0	0,01	0,02	0,03	0,04	0,06	0,07	0,08	0,1	0,2	4
Re(w)	1	0,94	0,76	0,49	0,206	-0,123	-0,177	-0,193	-0,181	-0,085	-0,003
Im(w)	0	-0,313	-0,577	-0,73	-0,739	-0,516	-0,397	-0,303	-0,179	-0,016	-0,001

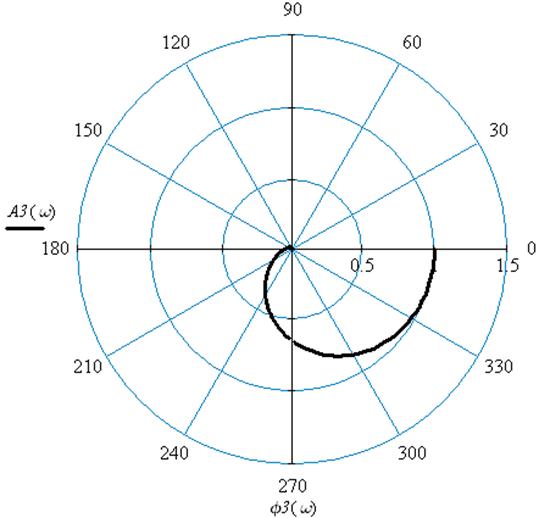
 Рис.16  Амплитудно-фазовая характеристика по каналу возмущения 3

Этап 2. Синтез замкнутой САУ с ПИ-регулятором

на заданную степень колебательности m=0.221

2.1 Расширенные частотные характеристики объекта управления по каналу регулирования.

Синтез замкнутой САУ осуществляется методом расширенных частотных характеристик.

Для определения расширенных частотных характеристик объекта по каналу регулирования необходимо в передаточной функции объекта сделать подстановку: p=-m·w+j·w, где m=0.221-заданная степень колебательности системы:

Передаточная  функция  по  каналу  регулирования  имеет  вид:

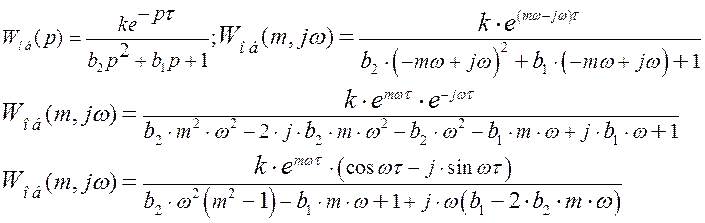
-расширенная амплитудно-частотная характеристика объекта по каналу регулирования

Выражение для расширенной амплитудно-частотной характеристики найдем как отношение модулей числителя и знаменателя:

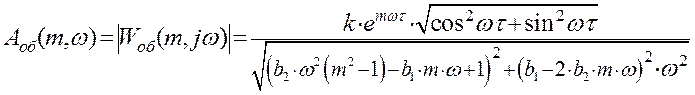
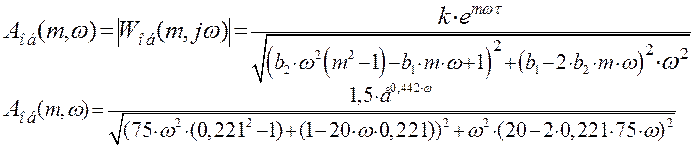
Расчетные данные для построения РАЧХ в Таблице 17. Расширенная АЧХ проходит выше обыкновенной АЧХ.                                                          

Таблица 17

w	0	0,005	0,01	0,03	0,04	0,05	0,1	0,2	0,3	0,5	1
A(m,w)	1,5	1,532	1,555	1,543	1,482	1,399	0,936	0,428	0,232	0,098	0,031
A(w)	1,5	1,48	1,452	1,274	1,164	1,053	0,609	0,225	0,099	0,027	0,002

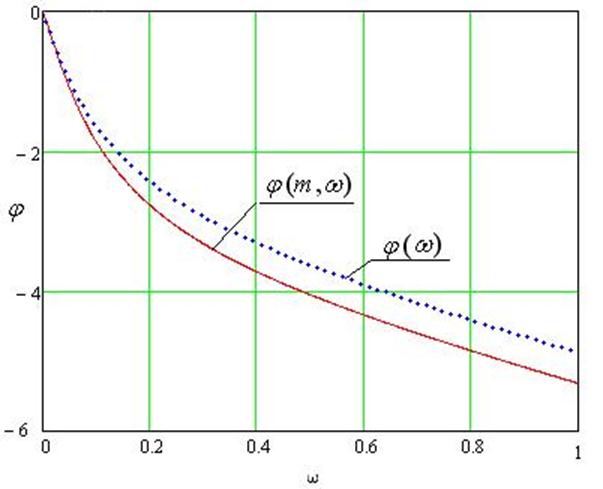
Рис.17 Расширенная амплитудно-частотная характеристика по каналу регулирования

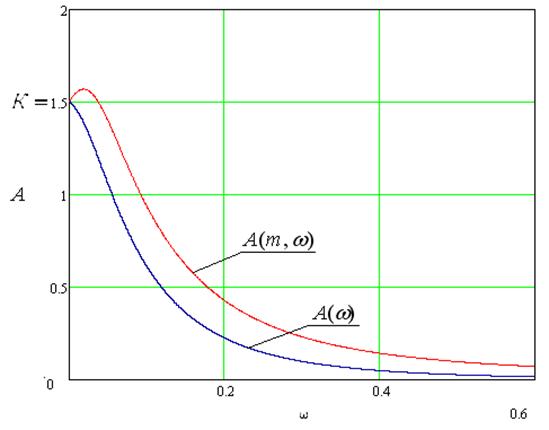
-расширенная фазо-частотная характеристика объекта по каналу регулирования

Выражение для расширенной фазо-частотной характеристики найдем как разность аргументов числителя и знаменателя:

 

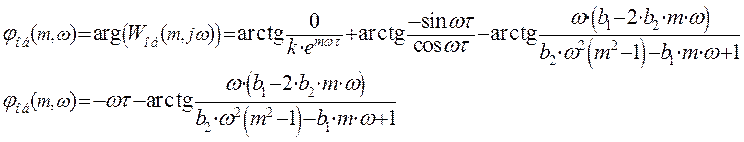
Функция 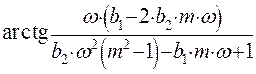 имеет две точки разрыва, в которых функция arctg изменяется с p/2 до -p/2, однако нас интересует поведение функции при положительном значении частоты ω. Чтобы найти эти точки, необходимо приравнять знаменатель функции к нулю.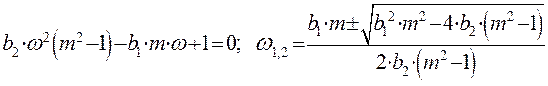                

Для обеспечения непрерывности графика РАФХ необходимо прибавить период, равный -p:

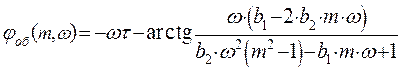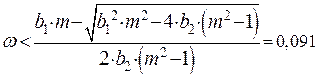
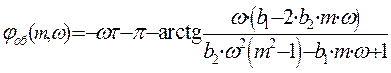 при

 при

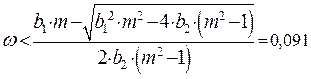
Расчетные данные для построения РФЧХ в Таблице 18. Расширенная ФЧХ проходит ниже обыкновенной ФЧХ.

Таблица 18

w	0	0,005	0,01	0,03	0,07	0,1	0,3	0,7	1	3
j(m,w)	0	-0,111	-0,224	-0,677	-1,442	-2,383	-3,321	-4,602	-5,316	-9,491
j(w)	0	-0,11	-0,219	-0,632	-1,286	-1,646	-2,935	-4,168	-4,878	-9,053

Рис.18 Расширенная фазо-частотная характеристика по каналу регулирования

2.2 Построение кривой равной степени колебательности m=0,221

Для реализации задачи синтеза САУ необходимо в плоскости настроек ПИ – регулятора построить кривую равной степени колебательности и на ней выбрать точку, соответствующую минимуму квадратичной интегральной оценки качества. Эта точка обычно находится при w_опт = 1.3 ^. w_max , где w_max – значение частоты w  в максимуме графика S₀(S₁).

Чтобы заданная система имела переходный процесс с заданной степенью колебательности m нужно, чтобы РАФХ заданной системы проходила через точку с координатами (-1, j^·0), т.е.:

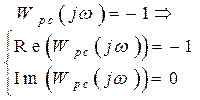
При этом степень колебательности будет равна m. Из этих условий найдем настройки пропорционально-интегрального регулятора. Для этого в передаточной функции регулятора сделаем  подстановку: p=-m·w+j·w,:

 

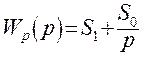
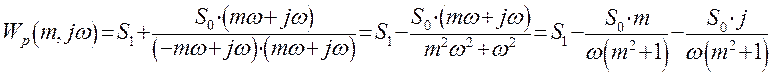
Представим передаточную функцию объекта в показательном виде:

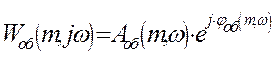
Используя уравнение Эйлера, получим:

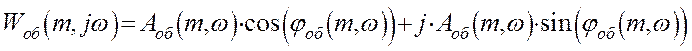
Поскольку передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора , следовательно, передаточную функцию разомкнутой системы можно также представить в показательном виде. В свою очередь, условия устойчивости  по критерию Найквиста представим в показательной форме, то есть мы можем составить систему из двух уравнений:

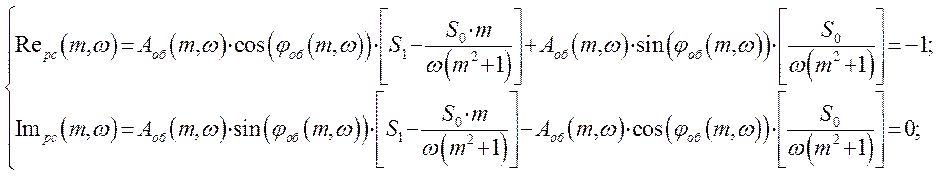
Можно получить область, где находятся значения настроечных параметров S₀, S₁, w.

Решая систему уравнений найдем настройки пропорционально-интегрального регулятора

Решение этой системы для S₀, S₁ :

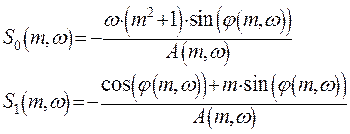
Используя полученные уравнения настроек регулятора, и задавая различные значениям w, получим кривую заданной степени колебательности m=0,221: