Для нахождения амплитудно-фазовой характеристики разомкнутой системы для правых настроек ПИ-регулятора выполним последовательность вычислений, аналогично приведенным выше.
Рис.49 АФХ разомкнутой системы с настройками, расположенными правее оптимальных, и t =0
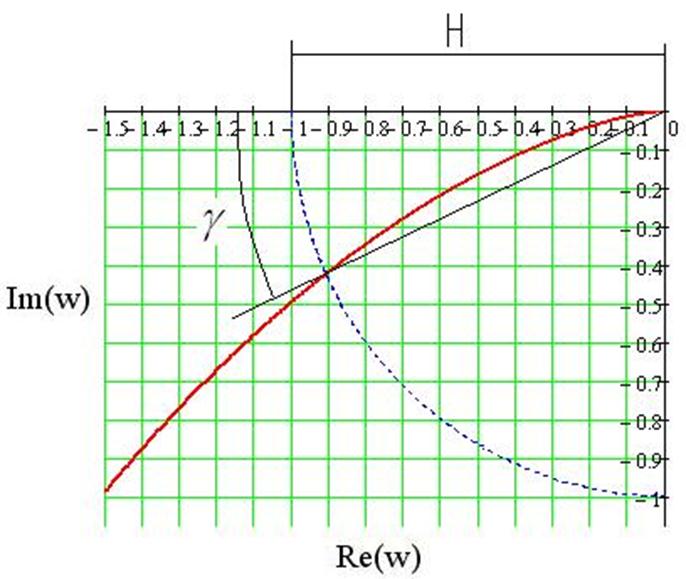
При настройках правее оптимальных: H=1, g =24°93'
Рис. 50 АФХ разомкнутой системы с оптимальными настройками, с настройками расположенными правее оптимальных, и с настройками расположенными левее оптимальных, и t =0
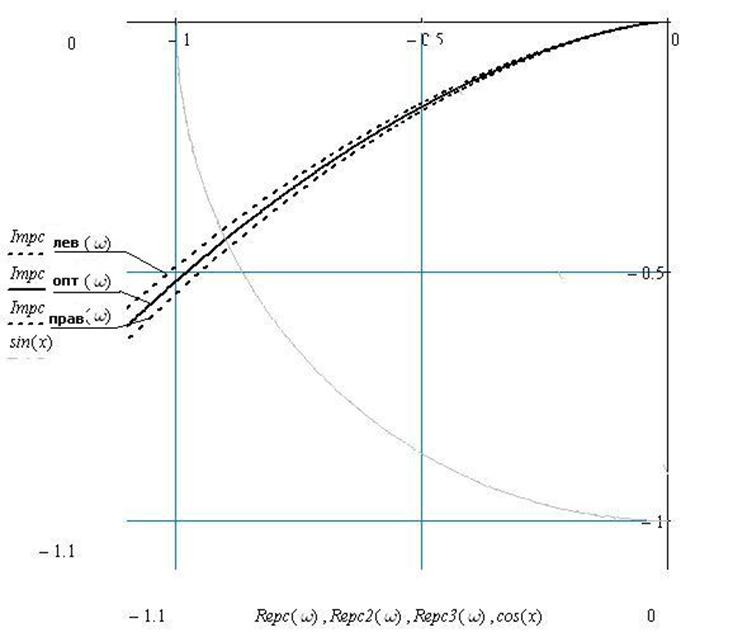
Заключение:
При настройках левее оптимальных: H=1, g =24°53'
При оптимальных настройках: H=1, g =24°74'
При настройках правее оптимальных: H=1, g =24°93'
О запасе устойчивости САУ можно судить по критерию Найквиста в следующей формулировке: если разомкнутая САУ устойчива, то для того, чтобы замкнутая САУ была устойчивой необходимо и достаточно, чтобы АФХ разомкнутой САУ не охватывала бы критическую точку с координатами (-1;j0).
В данном случае замкнутая САУ является устойчивой. Запас устойчивости по модулю Н и по фазе g при всех настройках регулятора является хорошим, т.к. отсутствует запаздывание. Но настройки, взятые правее оптимальных настроек, обеспечивают больший запас устойчивости системы.
3.2 Расчет переходного процесса в замкнутой системе автоматического регулирования по каналу управления
Построение переходного процесса в замкнутой системе автоматического регулирования без запаздывания по каналу управления для упрощения выполним с помощью следующего интеграла:
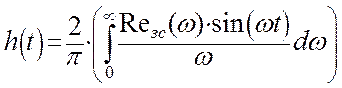
Построим переходные процессы в одних осях для настроек регулятора, взятых в оптимальной точке, правее и левее:
|
w |
S0(w) |
S1(w) |
|
|
Левые |
0,48438 |
0,647 |
12,2 |
|
Оптимальные |
0,51777 |
0,532 |
13,825 |
|
Правые |
0,54937 |
0,377 |
15,45 |
Рис.51 Переходный процесс замкнутой системы
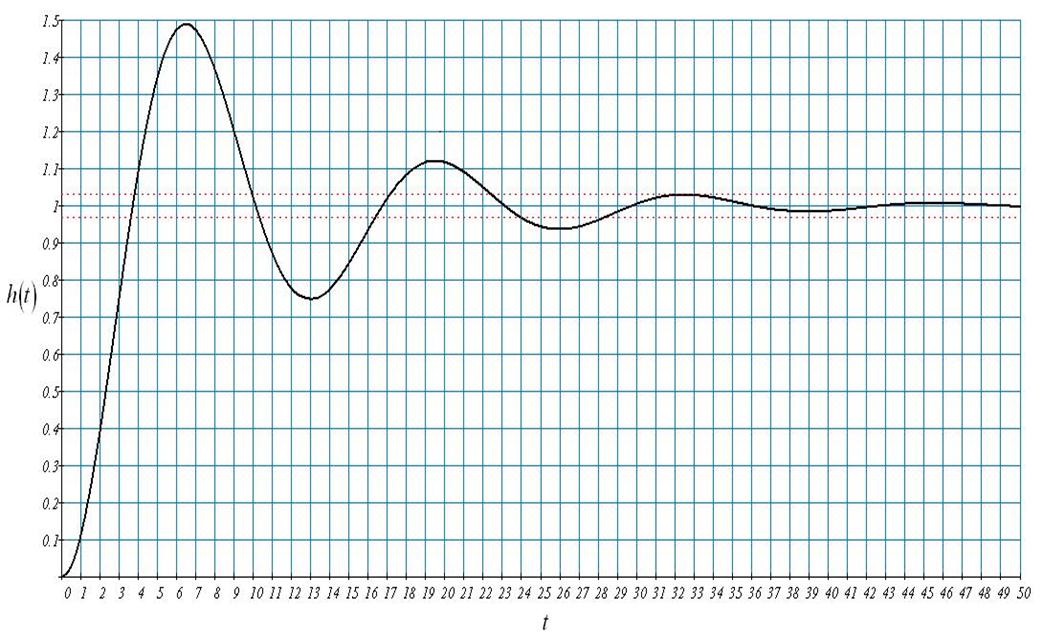при
настройках, расположенных левее оптимальных и t=0
По полученному графику определим показатели качества для переходного процесса без запаздывания и с настройками регулятора левее оптимальных настроек.
Время переходного процесса (регулирования) T = 36 с
Величина перерегулирования (динамическая ошибка) σ = 48,9 %
Квадратичная
интегральная оценка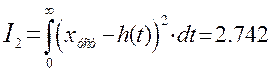 
Рис.52 Переходный процесс замкнутой системы
при оптимальных настройках и t=0
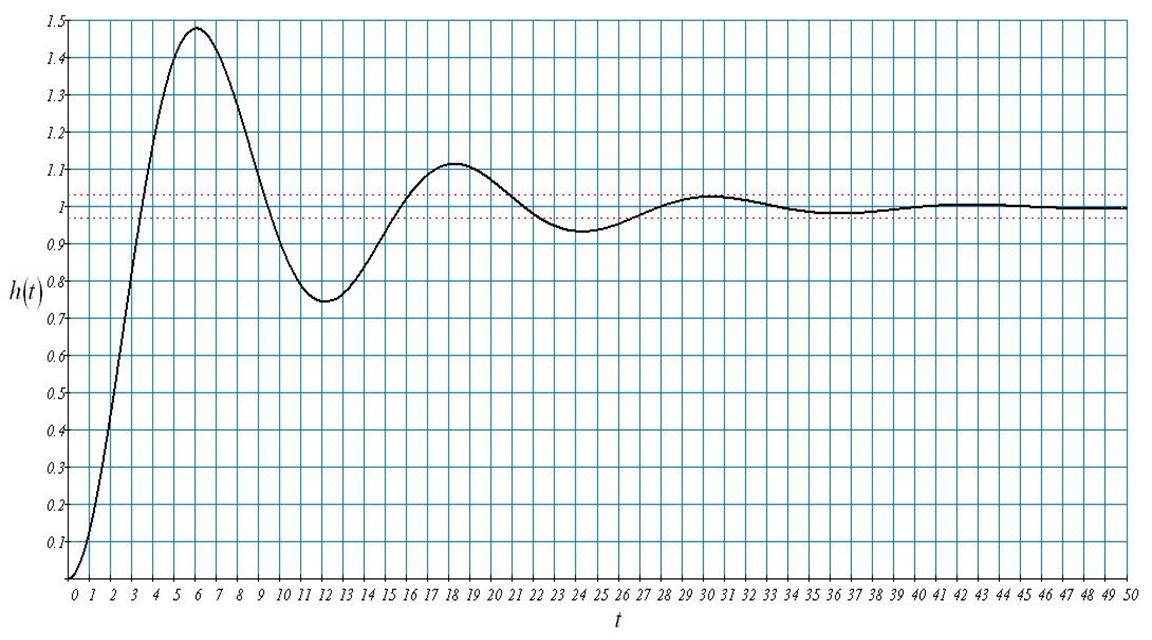По полученному графику определим показатели качества для
переходного процесса без запаздывания и с оптимальными настройками
регулятора.
Время переходного процесса T = 28 с
Величина перерегулирования σ = 47,7%
Квадратичная
интегральная оценка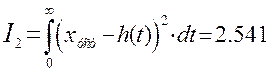 
Рис.53 Переходный процесс замкнутой системы при настройках, расположенных правее оптимальных и t=0.
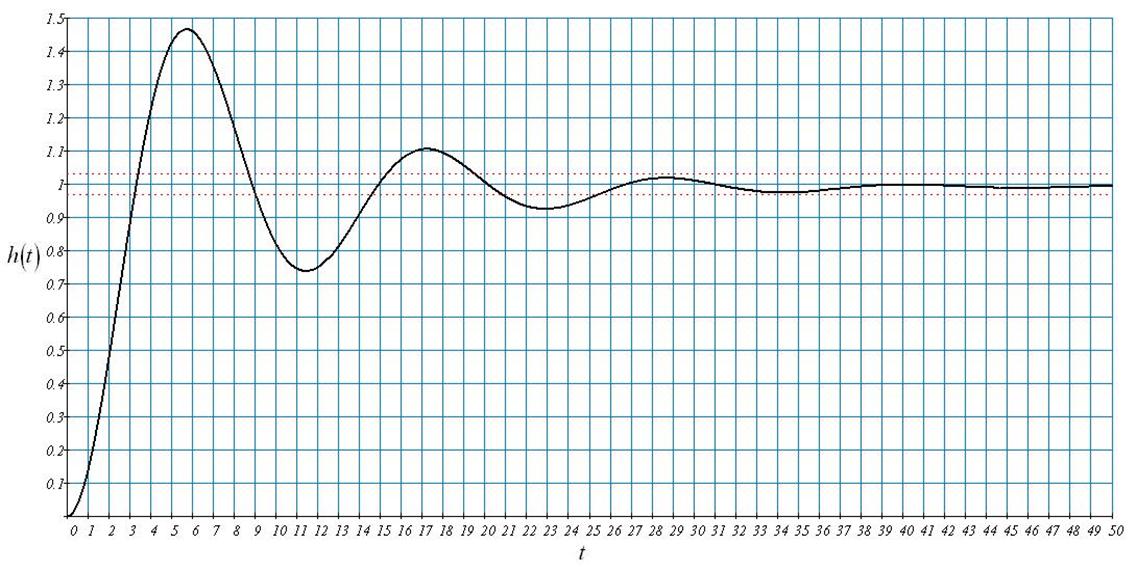
По полученному графику определим показатели качества для переходного процесса без запаздывания и с настройками регулятора правее оптимальных настроек.
Время переходного процесса T = 26,75 с
Величина перерегулирования σ = 46,6%
Квадратичная
интегральная оценка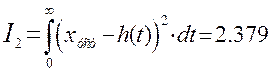 
С целью оценки влияния запаздывания по каналу управления при оптимальных настройках регулятора на характер переходного процесса (ПП) в замкнутой системе, изобразим в одних координатных осях график ПП с запаздыванием и график ПП без него.
Рис.54 Переходные процессы замкнутой системы по каналу управления с запаздыванием t=2 и без запаздывания.
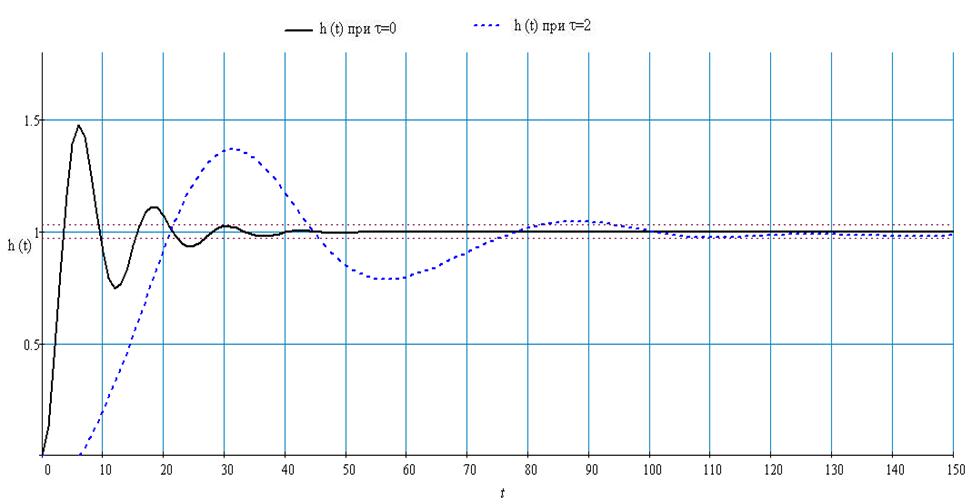
Таким образом, при появлении запаздывания в канале управления объекта регулирования график переходного процесса сдвигается по оси времени в положительном направлении на величину t чистого транспортного запаздывания, а так же увеличивается длительность и перерегулирование переходного процесса.
Теперь оценим влияние расположения настроек ПИ-регулятора на характер переходного процесса в системе при времени запаздывания, равном 0. Для этого изобразим в одних координатных осях три графика переходных процессов: при оптимальных настройках ПИ-регулятора, при настройках, взятых левее оптимальных и при настройках, взятых правее оптимальных.
Рис. 55. Переходный процесс замкнутой системы с тремя парами настроек
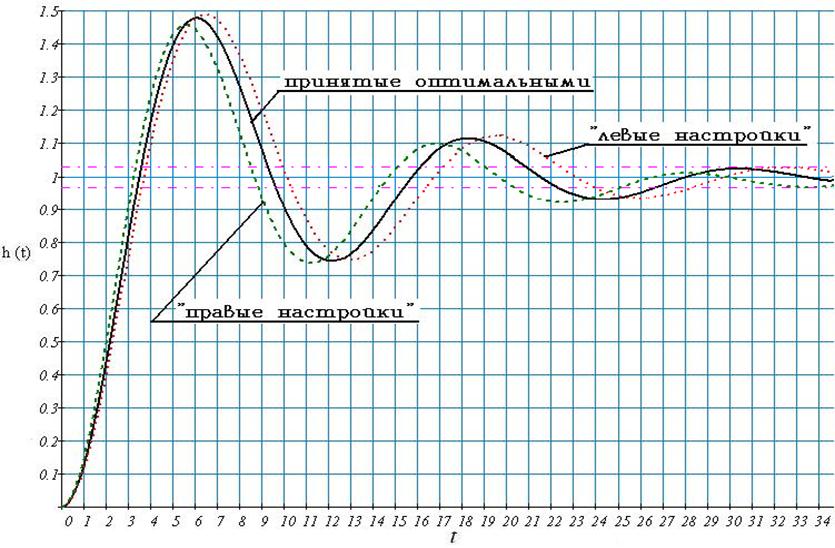
По графику видно, что оптимальные настройки регулятора обеспечивают наименьшую величину перерегулирования. Однако настройки регулятора, взятые левее, позволяют системе быстрее выйти в установившийся режим (в зону нечувствительности). Тем не менее, именно оптимальные настройки соответствуют минимуму квадратичной интегральной оценки качества на кривой равной степени колебательности в плоскости настроек ПИ – регулятора. Поэтому именно их будем использовать при дальнейших расчетах.
При анализе переходного процесса по каналу управления на возможное появление статической ошибки установлено следующее:
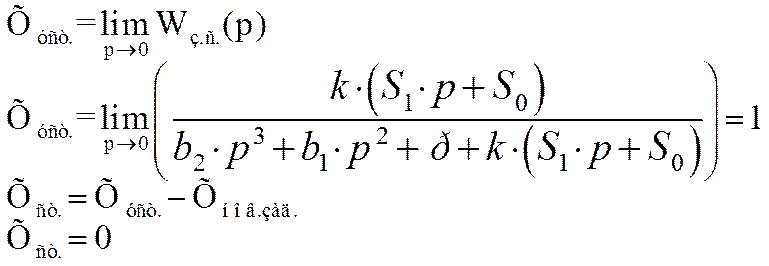
3.3 Расчет переходного процесса в замкнутой системе автоматического регулирования по каналам возмущения
Для построения переходного процесса в замкнутой системе по первому каналу возмущения предварительно выведем передаточную функцию:
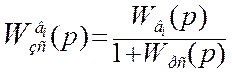
Представим в показательной форме:
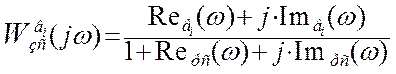
Построение переходного процесса в замкнутой системе автоматического регулирования по каналу возмущения выполним по интегралу:
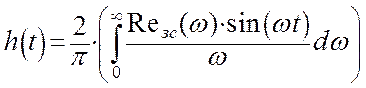
где Rзс(w) - вещественная частотная характеристика замкнутой системы, которая представлена в общем виде:
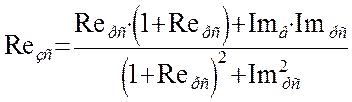
Приведем передаточную функцию к отношению произведений полиномов, подставив в формулу полученные ранее выражения передаточных функций: объекта по каналам управления, возмущения, и регулирования.
Передаточная функция замкнутой системы по первому каналу возмущения примет следующий вид:
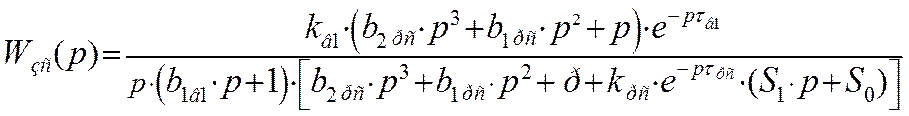
Найдем изображение переходной функции замкнутой системы:
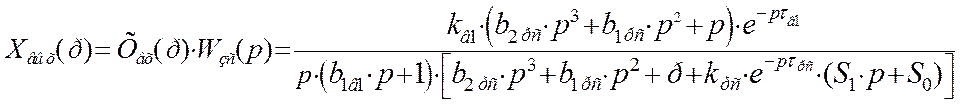
Воспользуемся теоремой о конечном значении оригинала для определения установившегося значения в переходном процессе замкнутой системы автоматического регулирования по каналу возмущения:
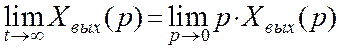
При
анализе переходного процесса по первому каналу возмущения на возможное
появление статической ошибки установлено следующее:
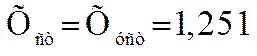
Квадратичная
интегральная оценка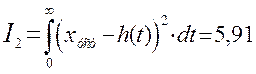 
Рис.56 Переходный процесс по первому каналу возмущения в системе с ПИ регулятором без запаздывания и с запаздыванием.
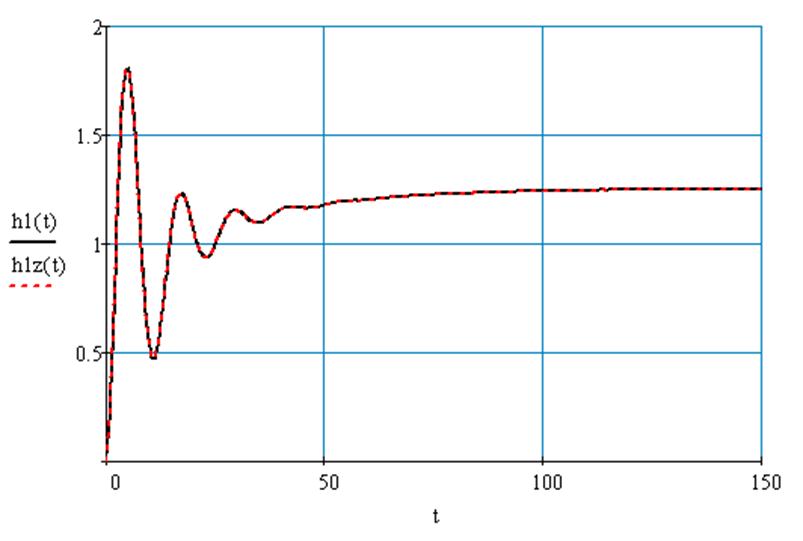
Для построения переходного процесса в замкнутой системе по второму каналу возмущения проделаем ту же последовательность преобразований:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.