Анализ и синтез замкнутой системы автоматического управления, страница 13

 Доминирующими полюсами являются П₁ П₂, П₅. Уменьшение амплитуды колебательной составляющей, создаваемое комплексными полюсами П₁ и П₅ зависит от модуля вещественной составляющей этих полюсов. Время регулирования переходной характеристики зависит от абсолютного значения вещественной части доминирующих полюсов, наибольшее значение из доминирующих полюсов оказывает П₂. Полюса П₃, П₄ оказывают малое влияние из-за удаленности от мнимой оси.

Время регулирования переходной характеристики также зависит от ноля Н₆, который оказывает сильное влияние. Время регулирования переходной характеристики также зависит от нулей Н₇, Н₈, Н_9. Ноль Н₆  оказывает существенное влияние. Нули Н₇, Н₈, Н₉ не оказывает существенного влияния из-за удаленности от мнимой оси.

Часть 3. Расчет системы автоматического управления

с И – регулятором и с П – регулятором для объекта,

не обладающего запаздыванием в канале регулирования

Этап 1. Анализ динамических свойств объекта,

не обладающего запаздыванием в канале регулирования,

во временной и частотной областях

Анализ динамических свойств объекта управления во временной и частотной областях по каналу регулирования и по трем каналам возмущения выполнен в первом этапе второй части пояснительной записки.

Этап 2. Синтез замкнутой САУ с И - регулятором и с П – регулятором

на заданную степень колебательности m=0,221

для объекта без запаздывания в канале регулирования

2.1 Расширенные частотные характеристики объекта управления по каналу регулирования

Синтез замкнутой САУ осуществляется методом расширенных частотных характеристик. Для определения расширенных частотных характеристик объекта по каналу регулирования необходимо в передаточной функции объекта сделать подстановку: p=-m·w+j·w, где m=0.221-заданная степень колебательности системы. Передаточная  функция  по  каналу  регулирования  имеет  вид:

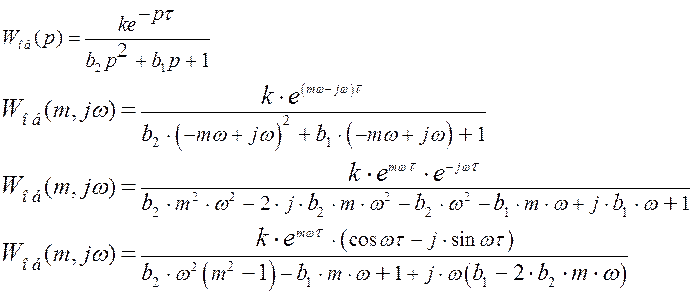
- расширенная амплитудно-частотная характеристика объекта по каналу регулирования

Выражение для расширенной амплитудно-частотной характеристики найдем как отношение модулей числителя и знаменателя:

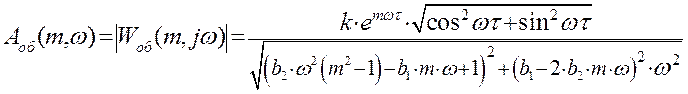
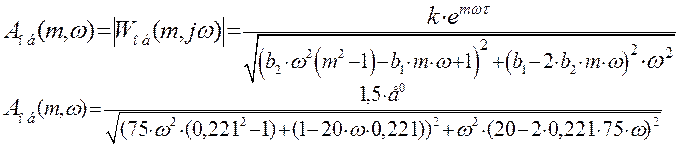
Расширенная АЧХ проходит выше обыкновенной АЧХ.

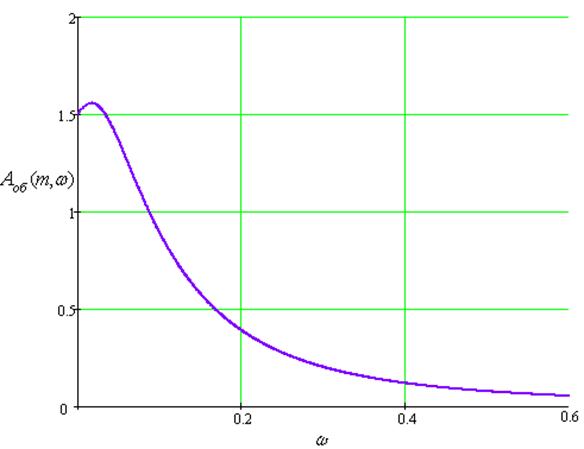
Расчетные данные для построения РАЧХ в Таблице 45.

Таблица 45

w	0	0,005	0,01	0,03	0,04	0,05	0,1	0,2	0,3	0,5	1
A(m,w)	1,5	1,529	1,548	1,523	1,456	1368	0,895	0,392	0,203	0,078	0,02

Рис.63 Расширенная амплитудно-частотная характеристика по каналу регулирования со степенью колебательности m=0,221 и без запаздывания.

- расширенная фазо-частотная характеристика объекта по каналу регулирования

Выражение для расширенной фазо-частотной характеристики найдем как разность аргументов числителя и знаменателя:

 

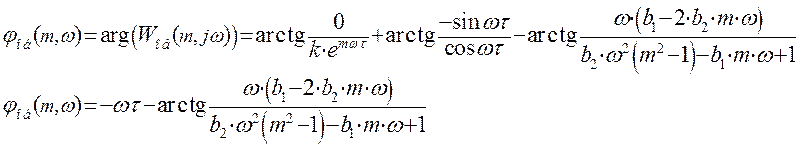
Функция 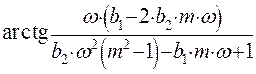 имеет две точки разрыва, в которых функция arctg изменяется с p/2 до -p/2, однако нас интересует поведение функции при положительном значении частоты ω. Чтобы найти эти точки, необходимо приравнять знаменатель функции к нулю.

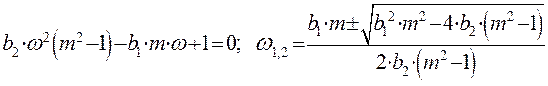
Для обеспечения непрерывности графика РАФХ необходимо прибавить период, равный -p:

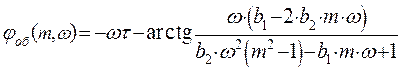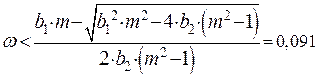
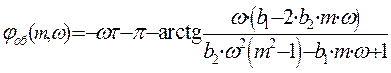 при

 при

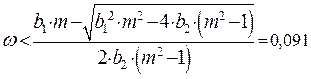
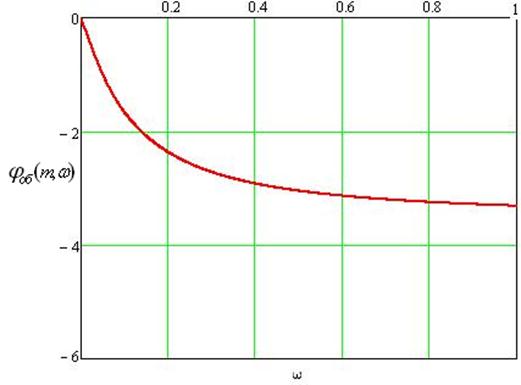
Расчетные данные для построения РФЧХ в Таблице 46. Расширенная ФЧХ проходит ниже обыкновенной ФЧХ.

Таблица 46

w	0	0,005	0,01	0,03	0,07	0,1	0,3	0,7	1	3
j(m,w)	0	-0,101	-0,204	-0,617	-1,302	-2,083	-2,721	-3,202	-3,316	-3,491

Рис.64 Расширенная фазо-частотная характеристика по каналу регулирования со степенью колебательности m=0,221 и без запаздывания.

2.3.  Построение кривой равной степени колебательности m=0,221 для объекта без запаздывания и выбор оптимальных настроечных параметров И - регулятора и П – регулятора.

Для реализации задачи синтеза САУ необходимо в плоскости настроек И – регулятора и в плоскости настроек П – регулятора построить кривую равной степени колебательности и на ней выбрать точку, соответствующую минимуму квадратичной интегральной оценки качества. Эта точка обычно находится при w_опт = 1.3 ^. w_max , где w_max – значение частоты w  в максимуме графика S₀(S₁).

Чтобы заданная система имела переходный процесс с заданной степенью колебательности m нужно, чтобы РАФХ заданной системы проходила через точку с координатами (-1, j^·0), т.е.:                                  

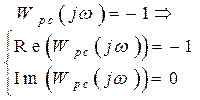
При этом степень колебательности будет равна m. Из этих условий найдем настройки пропорционально-интегрального регулятора. Для этого в передаточной функции регулятора сделаем  подстановку: p=-m·w+j·w,:

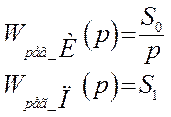
Представим передаточную функцию объекта в показательном виде:

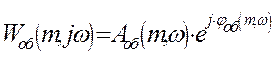
Используя уравнение Эйлера, получим:

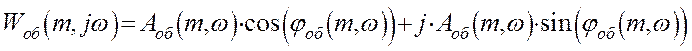
Поскольку передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора , следовательно, передаточную функцию разомкнутой системы можно также представить в показательном виде. В свою очередь, условия устойчивости  по критерию Найквиста представим в показательной форме, то есть мы можем составить систему из двух уравнений:

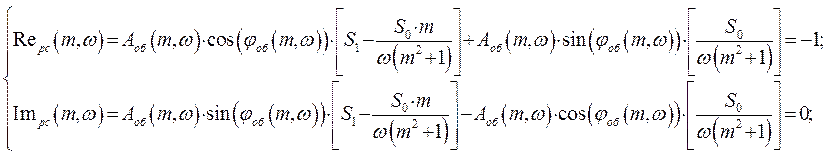
Можно получить область, где находятся значения настроечных параметров S₀, S₁, w.

Решая систему уравнений, найдем настройки интегрального регулятора

 и пропорционального регулятора.

Настройки И – регулятора:

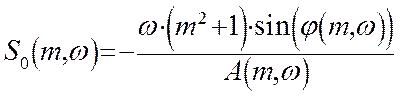
Настройки П – регулятора:

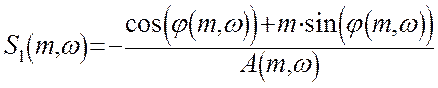
Используя полученные уравнения настроек И – регулятора и П - регулятора, и задавая различные значениям w, получим кривую заданной степени колебательности m=0,221.

Расчетные данные для построения кривой равной степени колебательности с И – регулятором  и с П – регулятором в Таблице 47

Таблица 47

w	0	0,03	0,05	0,1	0,2	0,39829	0,45	0,51777	0,55	0,6
S1	-0,667	-0,451	-0,265	0,349	2,219	8,45	10,627	13,825	15,484	18,232
S0	0	0,012	0,032	0,117	0,374	0,754	0,72	0,532	0,374	0,028

Оптимальные настройки для И – регулятора S0_опт = S0(m,w_опт) = 0,067