Анализ и синтез замкнутой системы автоматического управления, страница 6

Аппроксимация кривой вещественной частотной характеристики и выделение трапеций

Аппроксимируем полученную кривую ломаной линией и проводим через точки сопряжения отрезков ломаной горизонтальные прямые. Разбиение  графика  вещественной  частотной  характеристики  на трапеции, показано на Рис.2.22

Рис.22 Аппроксимация кривой переходного процесса в замкнутой системе

по каналу регулирования

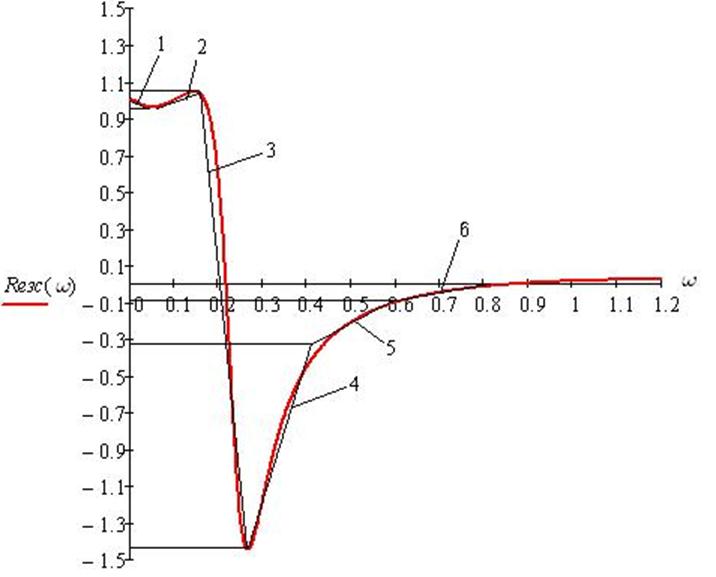
Следующим шагом является представление этой ВЧХ в асимптотическом виде. Начиная из точки Re_зс(0), аппроксимируем вещественную частотную характеристику прямолинейными отрезками 1,2,3,4,5,6 Концы каждого из этих отрезков соединим с осью ординат прямыми, параллельными оси абсцисс. Такую асимптотическую ВЧХ можно представить в виде 6 трапеций. Для каждой трапеции по графику определяем параметры частоту сопряжения w_d, частоту среза w₀ и высоту трапеции P. Величину P считаем положительной, если меньшая параллельная сторона трапеции расположена выше большей, в противоположном случае – отрицательной.

Характеристики трапеций, полученных в результате аппроксимации в Таблице 3.22

Таблица 22

Номер трапеции	1	2	3	4	5	6
P0	0,06	-0,1	2,48	-1,08	-0,23	-0,07
wd	0	0,05	1,05	0,27	0,34	0,61
w0	0,05	1,05	0,27	0,34	0,61	0,8
c	0	0,047	3,88	0,79	0,55	0,76

Построение h-функций.

Строим отдельные составляющие переходного процесса, используя таблицы h-функций.

Для каждой трапеции в соответствии с ее коэффициентом наклона боковой стороны производим построение единичного переходного процесса. Для перехода от единичного нормализованного процесса к реальному ординаты переходного процесса умножаются на соответствующие высоты трапеций P_0i. По оси времени откладывается t_ист.t/w_0i (где i -  номер трапеции).

Суммируя отдельные составляющие переходного процесса, получаем переходный процесс в замкнутой системе по каналу задание-выход

Рис.23 Составляющие переходного процесса (h-функции)

Рис.24 Переходный процесс в замкнутой системе по каналу задание – выход

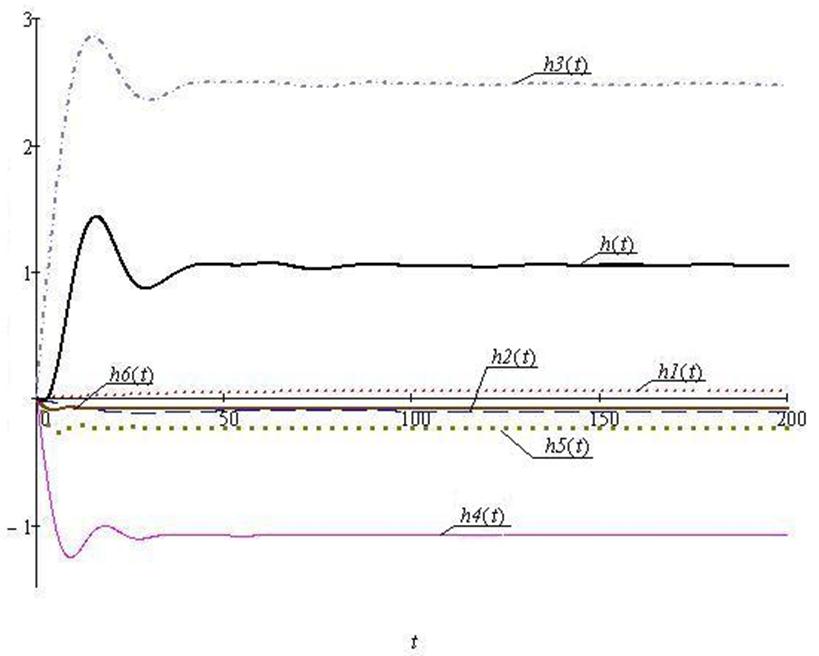
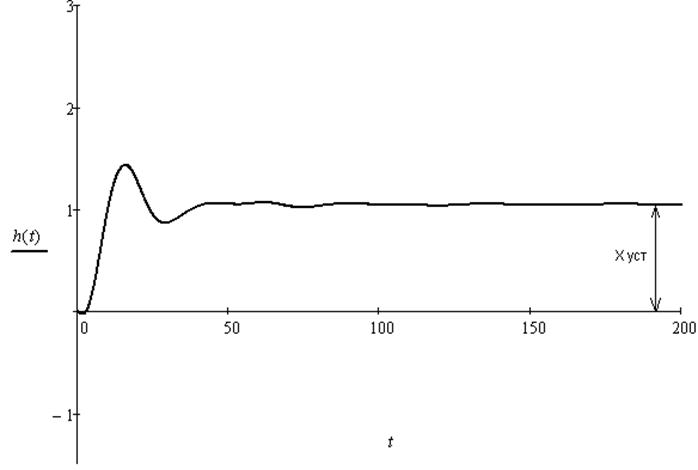
Переходный процесс в замкнутой системе по каналу задание – выход имеет колебательный характер со степенью колебательности m»0,221 и запаздыванием t=2. После окончания переходного процесса выходная величина выходит на установившееся значение Х_уст=1.

3.4. Построение переходного процесса в замкнутой системе по каналу возмущения 1

Воспользуемся формулой, которая позволяет найти переходный процесс через вещественную частотную характеристику системы:

     

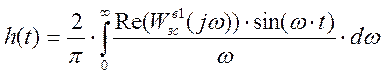
Передаточная функция замкнутой системы по каналу возмущения 1:

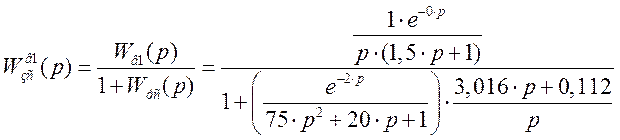
Производим замену: p=j×w

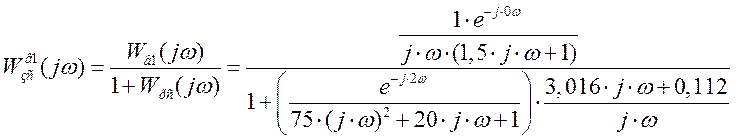
Расчетные данные (получены численным методом) для построения переходного процесса по каналу возмущение1 – выход в Таблице 23

Таблица 23

t	0	10	20	30	50	70	90	120	170	250
hвоз1(t)	0	3,462	4,219	4,589	4,984	5,201	5,34	5,473	5,603	5,71

t	500	3000	5000	6000	6500	6800
h(t)	5,829	5,931	5,94	5,941	5,943	5,943

Рис.25 Переходный процесс в замкнутой системе по каналу возмущение 1 - выход

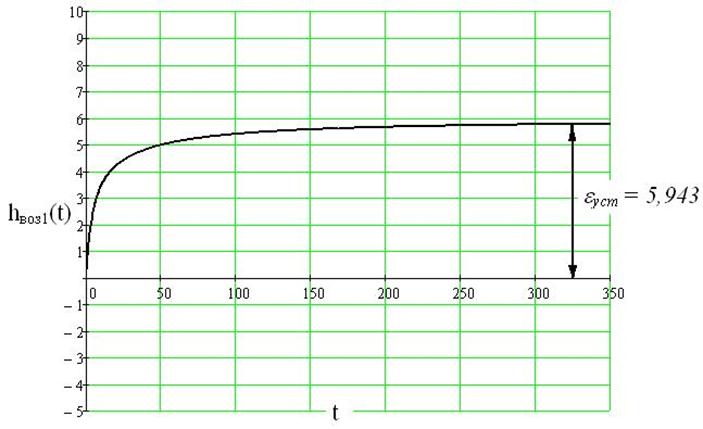
Переходный процесс в замкнутой системе по каналу возмущение 1 – выход имеет колебательный характер со степенью колебательности m»0,221 и запаздыванием t=0. После окончания переходного процесса выходная величина имеет статическую ошибку e_уст = 5,943.

3.5. Построение переходного процесса в замкнутой системе по каналу возмущения 2

Воспользуемся формулой, которая позволяет найти переходный процесс через вещественную частотную характеристику системы:

     

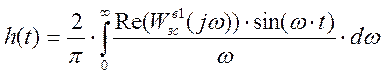
Передаточная функция замкнутой системы по каналу возмущения 2:

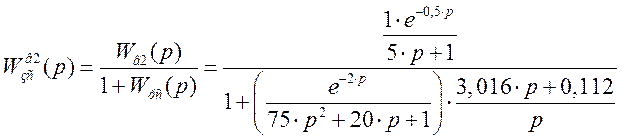
Производим замену: p=j×w

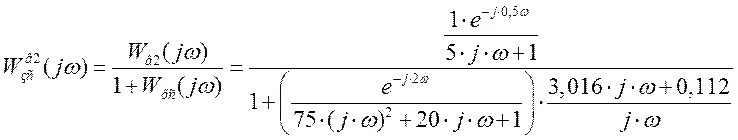
Расчетные данные для построения переходного процесса по каналу возмущение 2 – выход в Таблице 24.

Таблица 24

t	0	5	10	20	50	100	120	160	200	300	1000
hвоз2(t)	0	0,391	0,284	0,047	0,023	0,004	0,002	0,0003	0,0002	0,000003	0,00001

Рис.26  Переходный процесс в замкнутой системе по каналу возмущение 2 - выход

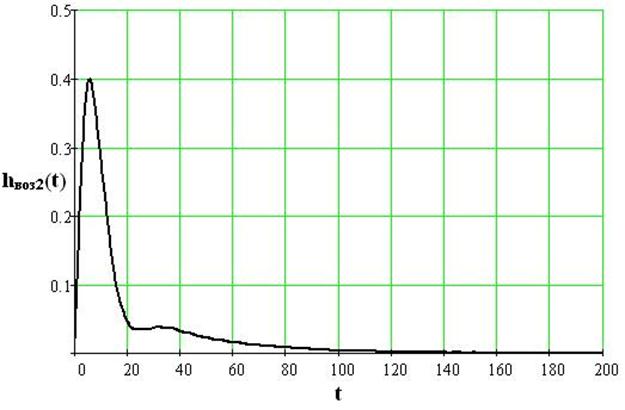
Переходный процесс в замкнутой системе по каналу возмущение 2 – выход имеет колебательный характер со степенью колебательности m»0,221 и запаздыванием t=0,5. После окончания переходного процесса выходная величина выходит на установившееся значение Х_уст=0.

3.6. Построение переходного процесса в замкнутой системе по каналу возмущения 3

Воспользуемся формулой, которая позволяет найти переходный процесс через вещественную частотную характеристику системы:

     

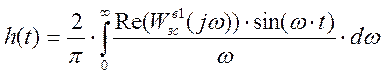
Передаточная функция замкнутой системы по каналу возмущения 3:

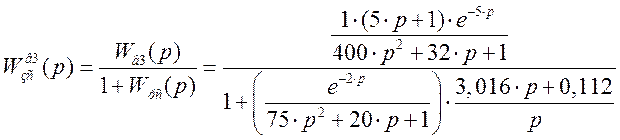
Производим замену: p=j×w

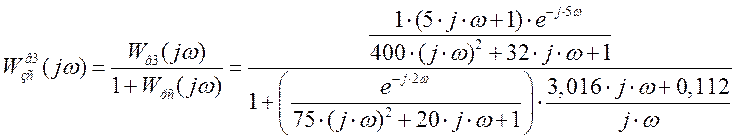
Расчетные данные для построения переходного процесса по каналу возмущение 3 – выход в Таблице 25.

Таблица 25

t	0	5	10	20	30	80	100	150	170
hвоз3(t)	0	0,126	0,125	0,079	0,091	0,017	0,0067	0,00053	0,00022

Рис.27 Переходный процесс в замкнутой системе по каналу возмущение 3 – выход

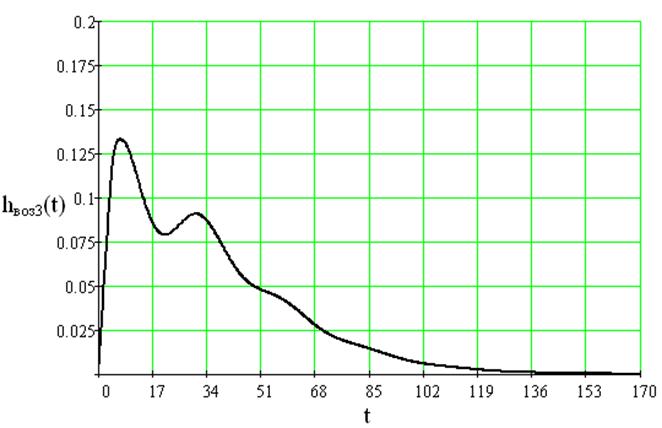
Переходный процесс в замкнутой системе по каналу возмущение 3 – выход имеет колебательный характер со степенью колебательности m»0,221 и запаздыванием в канале возмущения t=5. После окончания переходного процесса выходная величина выходит на установившееся значение Х_уст=0.