Анализ и синтез одноконтурных систем автоматического управления (САУ)

Содержание

Задачи курсовой работы по теории автоматического управления. 4

Исходные данные. 4

1.  Анализ динамических свойств объекта во временной и частотной областях. 6

1.1 Канал регулирования. 6

1.2 Первый канал возмущения. 10

1.3 Второй канал возмущения. 12

1.4 Третий канал возмущения. 16

2.  Синтез  замкнутой  САУ  с  ПИ-регулятором при τ = 1. 22

2.1  Построение  графиков  расширенных  амплитудно-частотной  и  фазо-частотной  характеристик. 22

2.2. Расчет  и  построение  кривой  с  заданной  степенью  колебательности   в  плоскости  настроек   ПИ-регулятора(S0-S1) 25

2.3 Определение оптимальных настроек ПИ-регулятора при τ =1. 26

2.4  Построение амплитудно-фазовой характеристики  разомкнутой системы определение запасов устойчивости по модулю и по фазе. 26

3.1 Построение  переходных  процессов при τ = 1. 28

3.1  Построение  переходного  процесса  в  замкнутой  системе  по  каналу  управления. 28

3.2 Расчет переходного процесса в замкнутой системе автоматического регулирования по каналам возмущения. 34

4. Анализ и синтез замкнутой САУ с ПИ-регулятором при τ=0. 41

4.1 Анализ свойств объекта при отсутствии запаздывания. 41

5. Определение оптимальных настроечных параметров пропорционально-интегрального регулятора. 44

5.1.Расчет расширенных частотных характеристик объекта по каналу регулирования. 44

5.2. Построение  кривой  с  заданной  степенью  колебательности   в  плоскости  настроек   ПИ-регулятора(S0-S1) 45

5.3 Определение оптимальных настроек ПИ-регулятора. 46

5.4  Построение амплитудно-фазовой характеристики  разомкнутой системы определение запасов устойчивости по модулю и по фазе. 47

6 Анализ замкнутой системы регулирования. 49

6.1 Построение переходного процесса с выбранными оптимальными настройками. 49

6.2 Построение переходного процесса с настройками выбранными левее оптимальных. 51

6.3 Построение переходного процесса с настройками выбранными правее оптимальных. 52

7  Построение переходных процессов в замкнутой системе по каналам возмущения при τ = 0. 55

7.1 Первый канал  возмущения. 55

7.2 Второй  канал  возмущения. 57

7.3 Третий   канал  возмущения. 58

8 Определение нулей и полюсов передаточных функций замкнутой системы.. 60

8.1 Канал управления. 60

8.2  Первый канал возмущения. 61

8.3  Второй канал возмущения. 62

8.4   Третий канал возмущения. 63

9 Анализ и синтез замкнутой САУ с ПД-регулятором, со степенью колебательности m=0.221 при условии, что τ=0 (индивидуальное задание) 65

10 Определение оптимальных настроечных параметров пропорционально-дифференциального регулятора. 65

10.1 Вывод формул для расчета настроек  ПД- регулятора – S2 и S1. 66

10.2 Выбор пар настроек ПД- регулятора. 67

10.3 Расчет амплитудно-фазовой характеристики разомкнутой системы и определение запасов устойчивости по модулю и фазе. 68

11. Расчет переходного процесса в замкнутой системе автоматического регулирования по каналу управления. 70

12. Расчет переходного процесса в замкнутой системе автоматического регулирования по каналам возмущения. 73

12.1  Первый канал возмущения. 73

12.2  Второй канал возмущения. 74

12.3  Третий канал возмущения. 75

13. Определение нулей и полюсов передаточных функций замкнутой системы по каналам управления и возмущения. 77

13.1 Канал управления. 77

13.2 Первый канал возмущения. 78

13.3  Второй канал возмущения. 79

13.4   Третий канал возмущения. 80

14. Анализ качества системы автоматического управления. 81

Список используемой литератуы.. 83

Задачи курсовой работы по теории автоматического управления

Курсовая работа посвящена анализу и синтезу одноконтурных систем автоматического управления (САУ) и состоит из следующих основных разделов:

1   анализ динамических свойств объекта управления во временной и частотной областях;

2   синтез замкнутой системы автоматического управления с пропорционально-интегральным регулятором, со степенью колебательности m=0,221;

3   построение переходных процессов в замкнутой системе автоматического управления по различным каналам с целью анализа ее качества;

4   синтез замкнутой системы автоматического управления с пропорционально-дифференциальным регулятором, со степенями колебательности m₁=0,147 иm₂=0,336;

5   построение переходных процессов в замкнутой системе автоматического управления с пропорционально-интегральным регулятором по одному из каналов возмущения с целью анализа ее качества.

Исходные данные

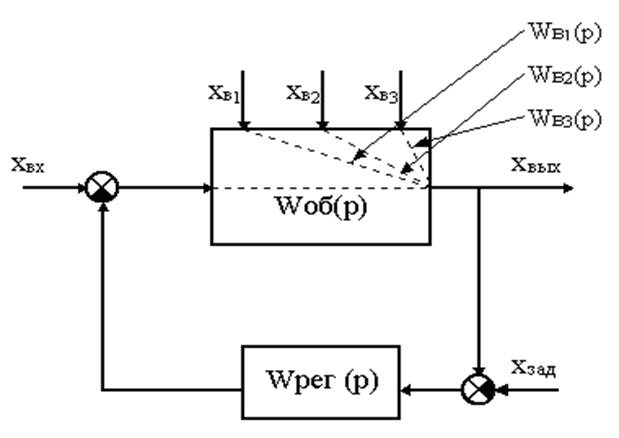
Рисунок 1 – Структурная схема системы автоматического управления

а) Вид передаточной функции по каналу регулирования:

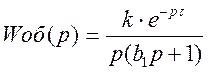 , где k = 1; b₁ = 5; τ = 1.

б) Вид передаточной функции по первому каналу возмущения:

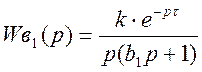 , где k = 0,5; b₁ = 1; τ = 0.

в) Вид передаточной функции по второму каналу возмущения:

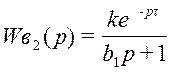 , где k = 0,5; b₁ = 6; τ = 3.

г) Вид передаточной функции по третьему каналу возмущения:

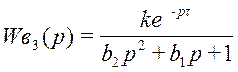 , где k = 0,5; b₂ = 400; b₁ = 32; τ = 10.

Анализ  и  синтез  замкнутой системы управления  необходимо  провести:

а) с  ПИ-регулятором  на  заданную  степень  колебательности  m=0,221.

б) с  типом  регулятора  и  условиями  расчета  его  настроек, выбираемыми  по  номеру  варианта  регулятора.

Номер  варианта  регулятора – 3:

Регулятор  ПД, выбрать три пары настроек S₁ – S₂ c кривой равной степени колебательности m=0,221 в области положительных значений настроек и диапазоне частот до частоты среза.

1.  Анализ динамических свойств объекта во временной и частотной областях

1.1 Канал регулирования

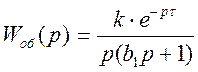, где k = 1; b₁ = 5; τ = 1

1.1.1 Построение переходного процесса:

Переходную функцию получаем при ступенчатом входном воздействии без учета чистого транспортного запаздывания, которое учтем в окончательной формуле. Расчет удобно  проводить  методом неопределённых коэффициентов   в  два  этапа.

;

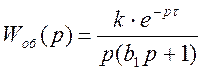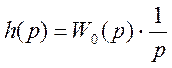
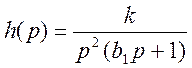
Разложим изображение на простые дроби:

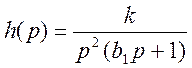
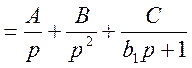
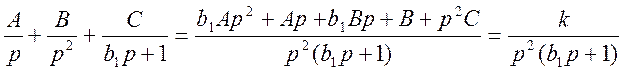
Найдём неизвестные коэффициенты разложения:

При :

При :  

При :  

Тогда:   ; ;  ;

Следовательно

;

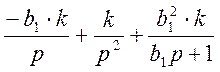Используя обратное преобразование Лапласа, получим оригинал переходной функции:

;

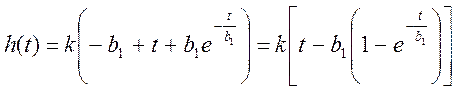Учитывая запаздывание получаем:

;

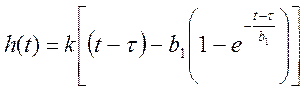Подставляя в полученную формулу k =1;  b₁ =5; τ =1, получаем переходную функцию по каналу регулирования:

;

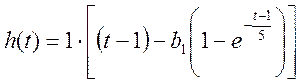Данные для построения переходного процесса по каналу регулирования представлены в таблице 1.1.

Таблица 1.1 

t	0	2.5	5	7.5	10	12.5	15	17.5	20
h(t)	0	0.217	1.233	2.887	4.827	7.02	9.327	11.733	14.161

График переходного процесса по каналу регулирования представлен на рис. 2.

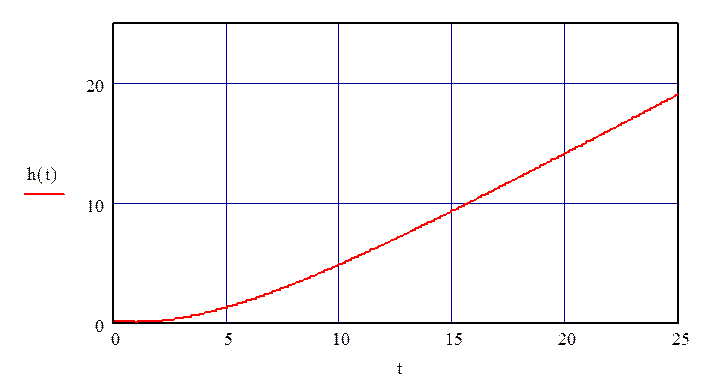
Рисунок 2 – переходная функция по каналу регулирования.     

1.1.2 Построение амплитудо-частотной характеристики:

Выражение для АЧХ:

;

;

;

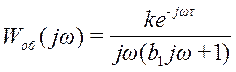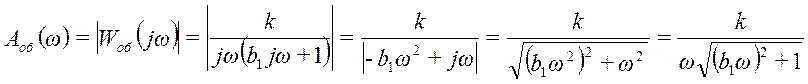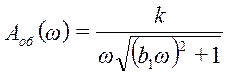         (1.2)

Подставляя в 1.2 исходные данные (k=1;  b₁=5; τ=1) получим:

;

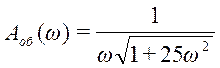Данные построения АЧХ канала регулирования представлены в таблице 1.2.

Таблица 1.2.