Анализ и синтез одноконтурных систем автоматического управления (САУ), страница 6

3.2.3  Третий   канал  возмущения

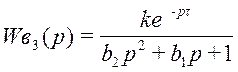 , где k = 0,5; b_3.2 = 400; b_3.1 = 32; τ = 10;

;

;

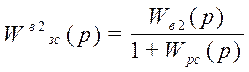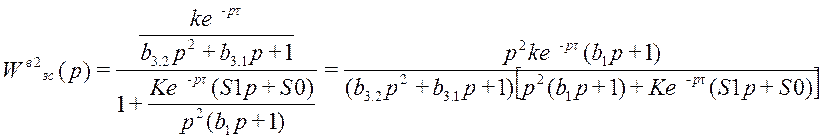S0=0.011, S1=0.295, b₁=5, K=1;

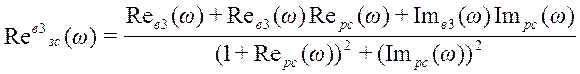,    где

;

;

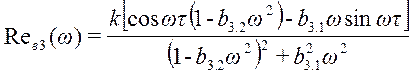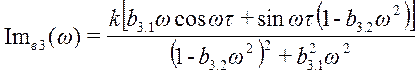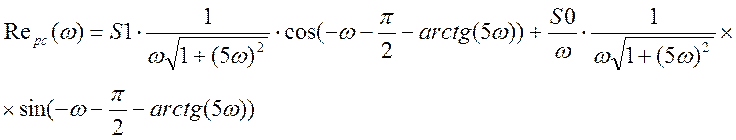
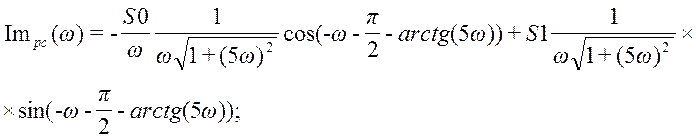
График ВЧХ замкнутой системы по третьему каналу возмущения (рис. 32).

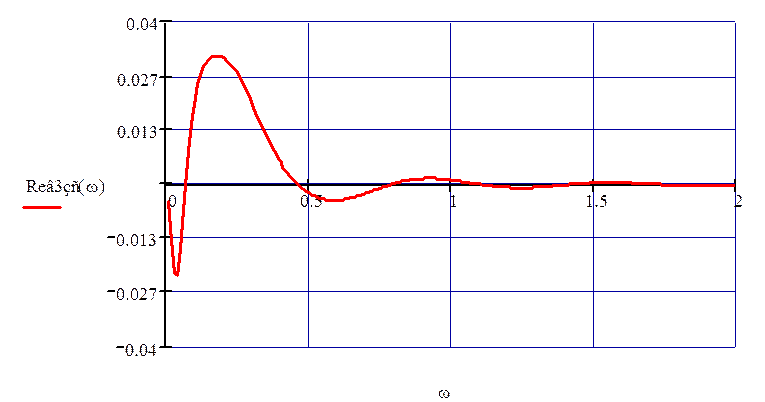
Рисунок 32 – График ВЧХ по третьему каналу возмущения

Рассчитаем переходный процесс по второму каналу возмущения с помощью следующего выражения:

;

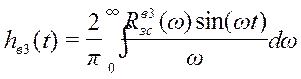Данные для построения переходного процесса по третьему каналу возмущения представлены в таблице 3.5

Таблица 3.5 

t	0	7	20	30	40	60	80	100	120
h(t)	0	0.018	-0.009	-0.016	-0.017	-0.012	-0.006	-0.002	-0.0004

Переходный процесс имеет вид представленный на рис. 33.

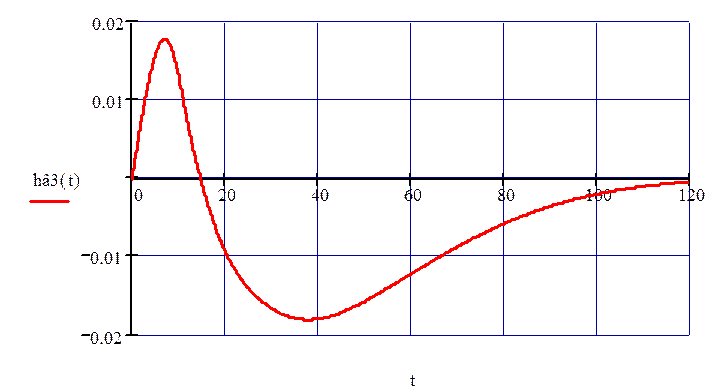
Рисунок  33 – Переходный процесс по третьему каналу возмущения

4.Анализ и синтез замкнутой САУ с ПИ-регулятором при τ=0

4.1 Анализ свойств объекта при отсутствии запаздывания

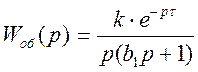, где k = 1; b₁ = 5; τ = 0;

4.1.1 Переходный процесс

Выражение для переходной функции было выведено выше и имеет следующий вид:

; 

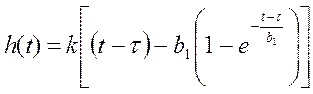Подставляя k =1;  b₁ =5; τ =0, получаем переходную функцию по каналу регулирования:

;

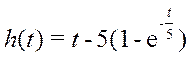Данные для построения переходного процесса по каналу регулирования представлены в таблице 4.1.

Таблица 4.1 

t	0	2.5	5	7.5	10	12.5	15	17.5	20
h(t)	0	0.532	1.807	3.615	5.655	7.91	10.344	12.651	15.092

График переходного процесса по каналу регулирования при отсутствии запаздывания представлен на рис. 34.

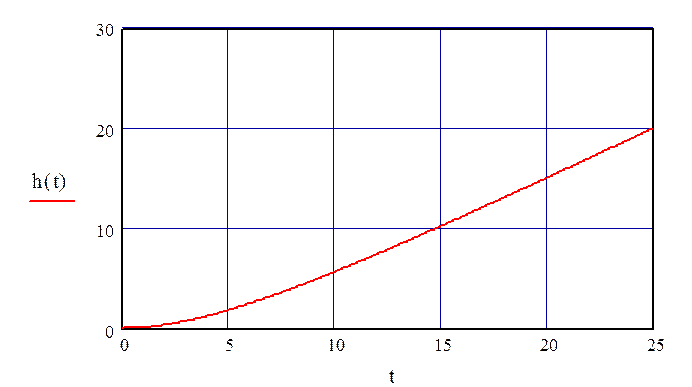
Рисунок 34 – переходного процесса по каналу регулирования при τ=0

4.1.2  Построение амплитудо-частотной характеристики:

Амплитудо-частотную характеристику построим по известной формуле:

;

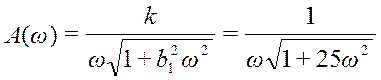Данные построения АЧХ канала регулирования представлены в таблице 4.2.

Таблица 4.2. 

ω	0.1	0.25	0.5	0.75	1.0	1.25	1.5	1.75	2.0
А(ω)	10	2.499	0.737	0.345	0.193	0.125	0.08	0.065	0.049

График АЧХ при τ=0 изображён на рис. 35.

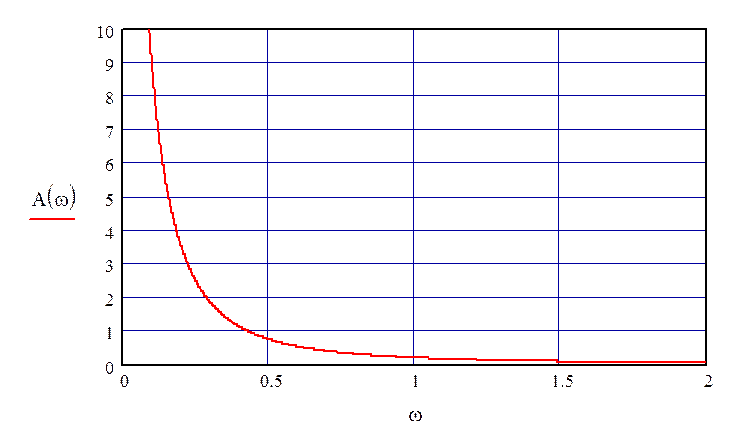
Рисунок 35 – АЧХ по каналу регулирования при τ=0

4.1.3  Построение фазо-частотной характеристики:

ФЧХ по  каналу регулирования определяется формулой:

;

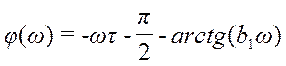Подставляя исходные данные k =1;  b₁ =5; τ =0, получаем:

;

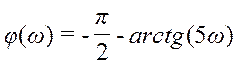Данные построения ФЧХ канала регулирования представлены в таблице 4.3.

Таблица 4.3. 

ω	0	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0
j(ω)	-1.57	-2.76	-2.95	-3.01	-3.04	-3.06	-3.07	-3.08	-3.09

График ФЧХ по каналу регулирования представлен на рис. 36.

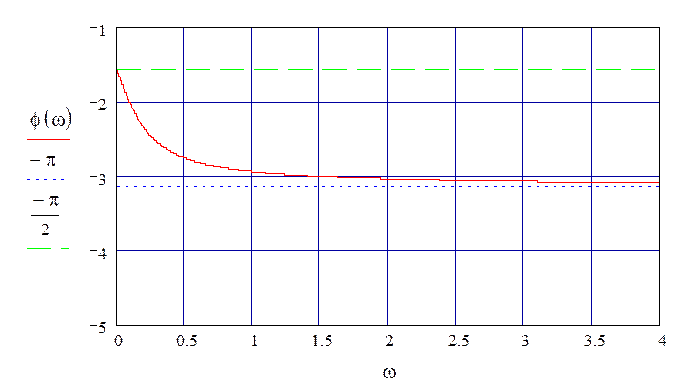
Рисунок 36 – ФЧХ по каналу регулирования при τ=0

4.1.4 Амплитудо-фазовая характеристика.

Для построения АФХ по каналу регулирования без запаздывания воспользуемся известными формулами:

;

  ;

где

; 

;

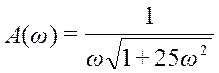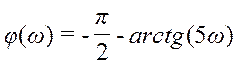Данные построения АФХ канала регулирования представлены в таблице 4.4.

Таблица 4.4. 

Re	-4.988	-4.706	-4.0	-2.5	-0.69	-0.294	-0.192
Im	-99.751	-18.824	-8.0	-2.5	-0.276	-0.074	-0.038
ω	0.01	0.05	0.1	0.2	0.5	0.8	1

График АФХ по каналу регулирования представлен на рис. 37.

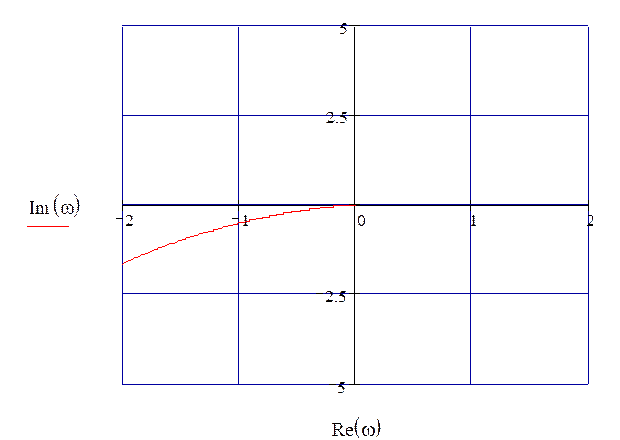
Рисунок 37 – АФХ по каналу регулирования при τ=0

5. Определение оптимальных настроечных параметров пропорционально-интегрального регулятора

5.1.Расчет расширенных частотных характеристик объекта по каналу регулирования.

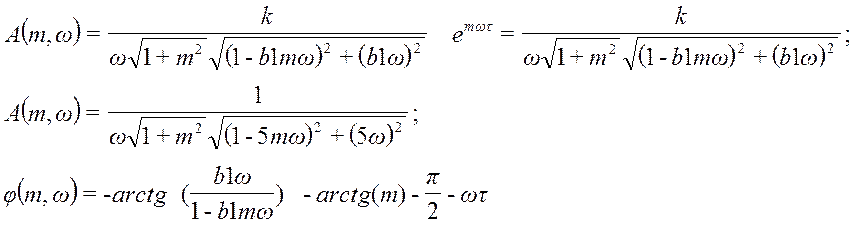Для построения  РАЧХ воспользуемся ранее выведенными формулами.

Данные для построения РАЧХ приведены в таблице 5.1.

 Таблица 5.1 

ω	0.01	0.2	0.4	0.6	0.8	1.0	1.2	1.4
А(m,ω)	98.8	4.03	1.27	0.617	0.36	0.24	0.18	0.13

На рис. 38 представлен график РАЧХ по каналу управления при отсутствии запаздывания.

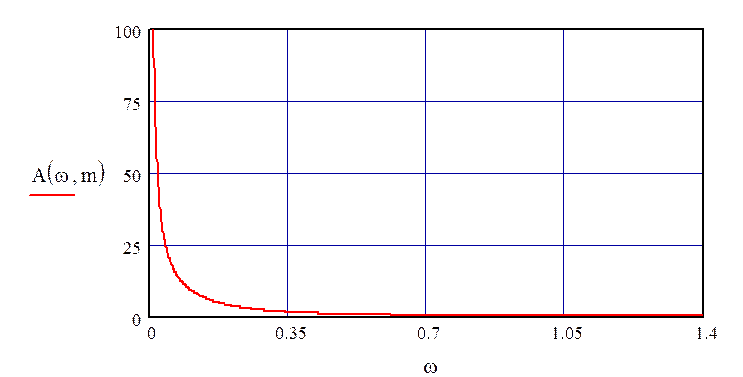
Рисунок  38 –  РАЧХ  по каналу управления

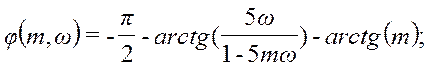 при ω < 0,905

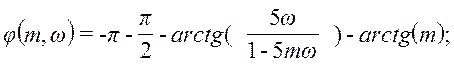при ω ≥ 0,905

Данные для построения РФЧХ приведены в таблице 2.2.

 Таблица 5.2 

ω	0	0.2	0.4	0.6	0.8	1.0	1.2	1.4
j(m,ω)	-1.79	-2.71	-3.09	-3.24	-3.33	-3.38	-3.41	-3.43

График полученной РФЧХ имеет вид, представленный на рис. 39.

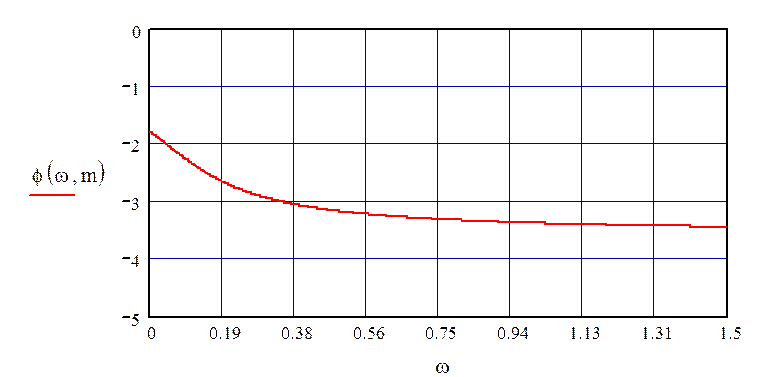
Рисунок 39  –  РФЧХ по каналу управления

5.2. Построение  кривой  с  заданной  степенью  колебательности   в  плоскости  настроек   ПИ-регулятора(S0-S1)

Воспользуемся формулами:

;

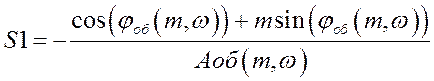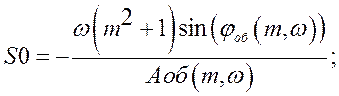
Данные для построения плоскости настроек ПИ-регулятора представлены в таблице 2.3.

Таблица 2.3

S0	0	0.007	0.016	0.023	0.032	0.013		0.019		0
S1	0	0.076	0.165	0.255	0.502	0.942		1.054		0
ω	0	0.05	0.15	0.20	0.25	0.30		0.40		0.45

Плоскость настроек ПИ-регулятора при τ = 0 имеет вид, представленный на рис. 40.

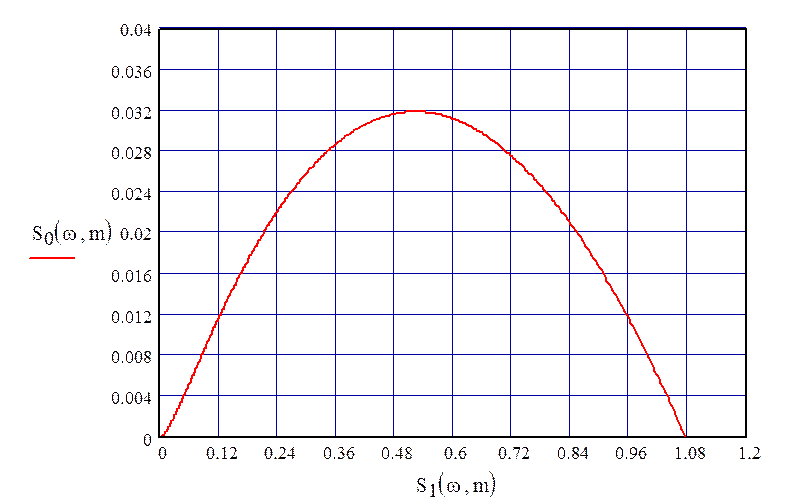
Рисунок 40  – Плоскость настроек ПИ-регулятора

5.3 Определение оптимальных настроек ПИ-регулятора

Оптимальные настройки ПИ-регулятора, обеспечивающие при заданной степени колебательности m минимизацию квадратичной интегральной оценки J₂ переходного процесса в замкнутой системе, определяются, как координаты точки, лежащей на правой ветви кривой S₀-S₁ вблизи её вершины. Найти положение этой точки можно при помощи следующего равенства: