Анализ и синтез одноконтурных систем автоматического управления (САУ), страница 11

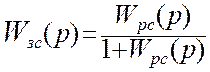
Определение полюсов передаточной функции необходимо производить для каждого сомножителя характеристического полинома отдельно.

13.1 Канал управления

;

;

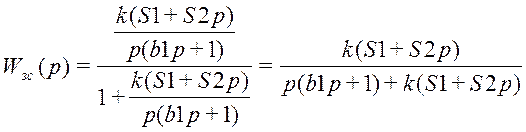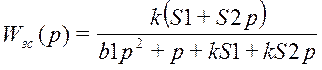Нули передаточной функции:

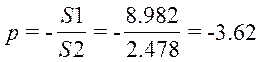
Полюса передаточной функции:

Решением этого квадратного уравнения являются два сопряжённых корня:

где , а m=0.221;

;

;

Изобразим на комплексной плоскости полюса и нули передаточной функции (рис. 74).

Рисунок 74 – Нули и полюса передаточной функции ЗС по каналу регулирования

13.2 Первый канал возмущения

;

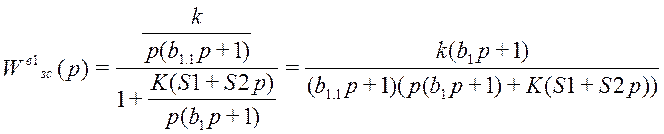где k = 0,5; b_1.1 = 1; S1=8.982, S2=2.478, b₁=5, K=1;

;

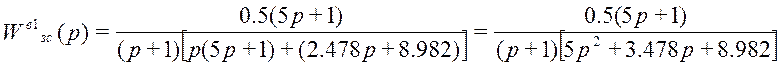Нули передаточной функции:

Полюса передаточной функции:

Решением этого квадратного уравнения являются два сопряжённых корня:

где , а m=0.221;

;

;

Третий полюс получим решая уравнение ;

Изобразим на комплексной плоскости полюса и нули передаточной функции (рис. 75).

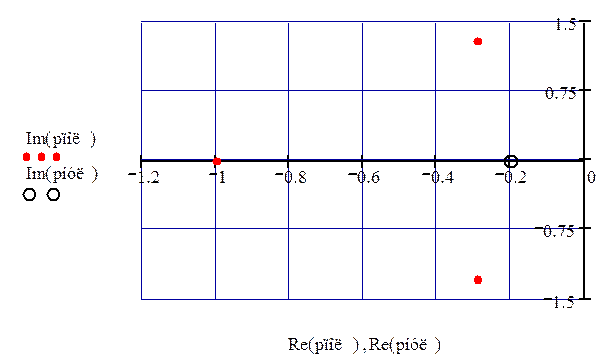
Рисунок 75 – Нули и полюса передаточной функции ЗС по первому каналу возмущения

13.3  Второй канал возмущения

;

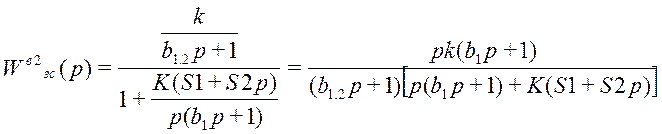где k = 0,5; b_1.2 = 6; S0=0.00505, S1=1.026, b₁=5, K=1;

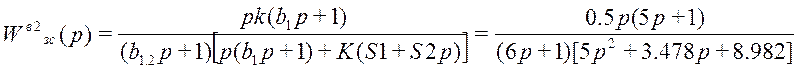
Нули передаточной функции:

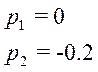
Полюса передаточной функции:

Решая уравнение,  найдем

;

;

Решением этого квадратного уравнения являются два сопряжённых корня:

;

;

где , а m=0.221;

;

;

Изобразим на комплексной плоскости полюса и нули передаточной функции (рис. 76).

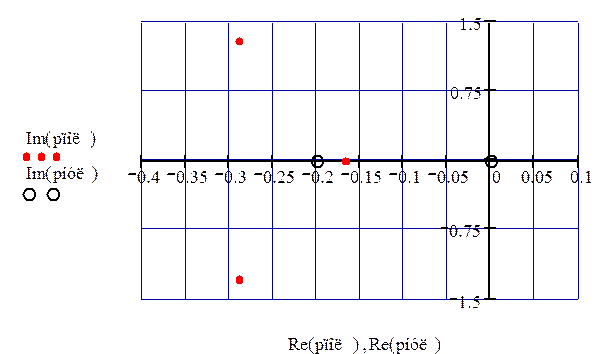
Рисунок 76 –  Нули и полюса передаточной функции ЗС по второму каналу возмущения

13.4   Третий канал возмущения

;

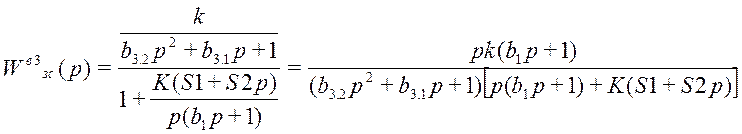где k = 0,5; b_3.2 = 400; b_3.1 = 32; S0=0.00505, S1=1.026, b₁=5, K=1;

;

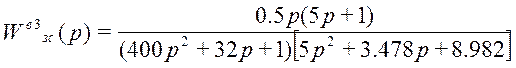Нули передаточной функции:

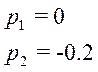
Полюса передаточной функции

Решая уравнение,  найдем:

;

;

;

;

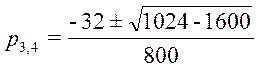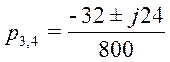Решением этого квадратного уравнения являются два сопряжённых корня:

;

;

где , а m=0.221;

;

;

Изобразим на комплексной плоскости полюса и нули передаточной функции      (рис. 77).

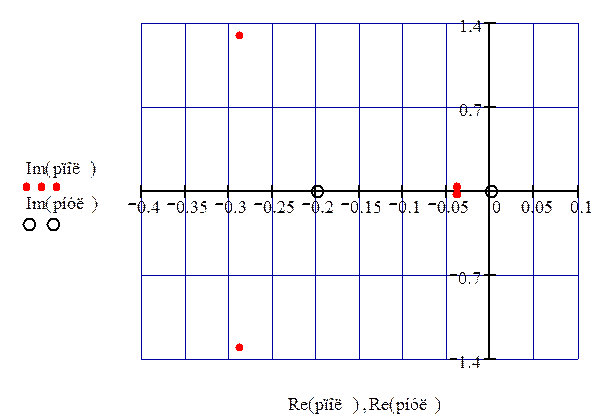
Рисунок 77 – Нули и полюса передаточной функции ЗС по третьему каналу возмущения

14. Анализ качества системы автоматического управления

В общем случае к числу характеристик определяющих качество процессов регулирования, относятся следующие: динамическая погрешность регулирования, которая представляет собой максимальное отклонение регулируемой величины от установившегося значения в переходном процессе, время и длительность процесса регулирования, статическая ошибка регулирования или остаточное отклонение регулируемой величины.

На качество процессов автоматического регулирования оказывают влияние корни характеристического уравнения системы. В каждом конкретном случае качество процесса регулирования определяется динамическими свойствами объекта, типом автоматического регулятора,  установкой числовых значений настроечных параметров регулятора. Проанализируем влияние различных параметров на качество системы автоматического регулирования:

1.  Запаздывание в канале регулирования ухудшает качество процессов регулирования. При его появлении уменьшается запас устойчивости по фазе и по модулю (тогда как запас устойчивости по модулю в системе без запаздывания максимален), причем при увеличении запаздывания система может выйти на границу устойчивости. Кроме того, запаздывание увеличивает время переходного процесса и уменьшает собственную частоту колебаний. Анализируя кривые настроек ПИ – регулятора, можно сделать вывод, что появление запаздывания уменьшает значения настроечных параметров регулятора.

2.     Запаздывание в канале возмущения не влияет на форму переходного процесса, но смещает его на время, равное транспортному запаздыванию, т.е. величине запаздывания возмущения. Что показано на рис. 53.

3.  Настроечные параметры, расположенные левее оптимальных увеличивают динамическую ошибку, увеличивают время переходного процесса, уменьшают запас устойчивости по фазе, не влияя при этом на запас устойчивости по модулю, а так же приближают комплексно-сопряженные полюса к мнимой оси. Настроечные параметры, расположенные правее оптимальных, влияют на выше перечисленные свойства обратным образом. Из графиков АФХ разомкнутой системы и анализа средней квадратичной ошибки отклонения видно, что правые настройки улучшают запас устойчивости по фазе (рис. 67).

4.  Инерционность канала возмущения объекта влияет на качество регулирования. Анализируя переходные процессы по различным каналам возмущения, мы видим, переходный процесс в замкнутой системе по каналу возмущения с инерционностью является наилучшим. Чем больше инерционность, тем быстрее регулятор компенсирует возмущающее воздействие.

5.  Анализируя взаимное расположение нулей и полюсов и соответствующие переходные процессы можно сделать следующие выводы:

-  близко расположенные нуль и полюс взаимно компенсируются и не влияют на вид переходного процесса;

-  наибольшее влияние на характер переходного процесса оказывают полюса, расположенные ближе к мнимой оси (они называются доминирующими);

           6.      Переходный процесс по каналу регулирования в системе с ПД-регулятором в отличие от переходного процесса по каналу регулирования в системе с ПИ-регулятором имеет статическую ошибку, которая при увеличении настроек регулятора уменьшается. Более того, в системе имеется канал возмущения, приводящий замкнутую систему к режиму незатухающих колебаний – первый канал возмущения. Сравнивая переходные процессы по каналу регулирования для систем с ПИ и ПД регуляторами, делаем вывод: динамическая ошибка в обоих случаях имеет один порядок, но время переходного процесса и квадратичная ошибка для ПД-регулятора меньше.

Список используемой литератуы

1. "Расчет линейных систем автоматического управления ". Методические указания к выполнению курсовой работы по теории автоматического управления. -Ярославль, ЯПИ, 1981;

2. "Динамические звенья автоматических систем и их характеристики. Понятие о типовом динамическом звене. Группа позиционных звеньев." Методические указания для самостоятельной работы студентов специальности 2102 по курсу "Теория автоматического управления"/Сост. Н.Н.Василькова. -Ярославль, ЯПИ, 1989;

3. Бесекерский В.А., Попопв Е.П. "Теория систем автоматического регулирования. " -М., Наука, 1975;

4. Иващенко Н.Н. "Автоматическое регулирование."-М., Машиностроение, 1972;