где k = 0,5; b3.2 = 400; b3.1 = 32; S0=0.00505, S1=1.026, b1=5, K=1;
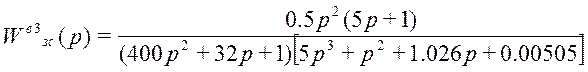
Нули передаточной функции:
![]()
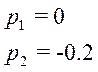
Полюса передаточной функции
Решая
уравнение, ![]() найдем:
найдем:
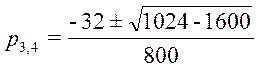 ;
;
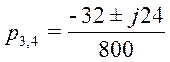 ;
;
![]() ;
;
![]()
Решая
уравнение ![]() , найдем
, найдем
![]() ;
;
![]() ;
;
![]()
Изобразим на комплексной плоскости полюса и нули передаточной функции
(рис. 59)
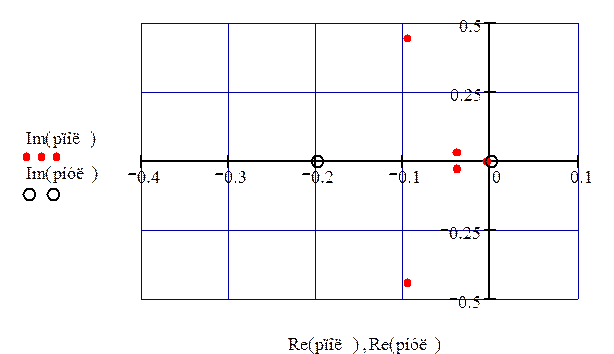
Рисунок – 59 нули и полюса третьего канала возмущения
9Анализ и синтез замкнутой САУ с ПД-регулятором, со степенью колебательности m=0.221 при условии, что τ=0 (индивидуальное задание)
Анализ свойств объекта по каналу регулирования
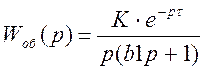
Данный анализ полностью проведён во второй части записки (для ПИ-регулятора), воспользуемся в дальнейшем выведенными ранее выражениями.
10 Определение оптимальных настроечных параметров пропорционально-дифференциального регулятора
Для определения расширенных частотных характеристик объекта по каналу регулирования в передаточную функцию сделаем подстановку:
![]() ,
,
где m - заданная степень колебательности системы , m=0.221;
w - частота (0≤w≤∞);
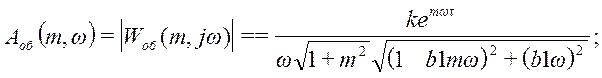
Выражение для расширенной амплитудно-частотной
характеристики :
График РАЧХ представлен на рис. 60.
Данные для построения РАЧХ приведены в таблице 10.1.
Таблица 10.1
|
ω |
0.01 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
1.4 |
|
А(m,ω) |
98.8 |
4.03 |
1.27 |
0.617 |
0.36 |
0.24 |
0.18 |
0.13 |
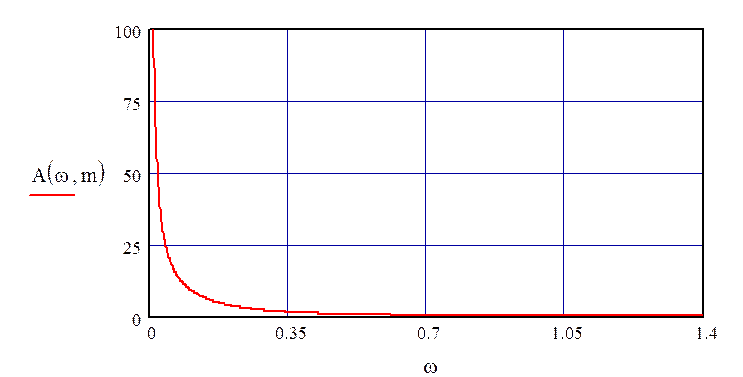
Рисунок 60 – РАЧХ объекта по каналу регулирования при τ=0
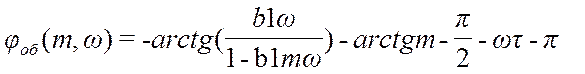
Выражение для расширенной фазо-частотной
характеристики:
Для обеспечения непрерывности фазо-частотной характеристики после точки разрыва 1/b1m=0,905 прибавляем период -p.
Данные для построения РФЧХ приведены в таблице 10.2.
Таблица 10.2
|
ω |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
1.4 |
|
j(m,ω) |
-1.79 |
-2.71 |
-3.09 |
-3.24 |
-3.33 |
-3.38 |
-3.41 |
-3.43 |
График РФЧХ представлен на рис. 61.
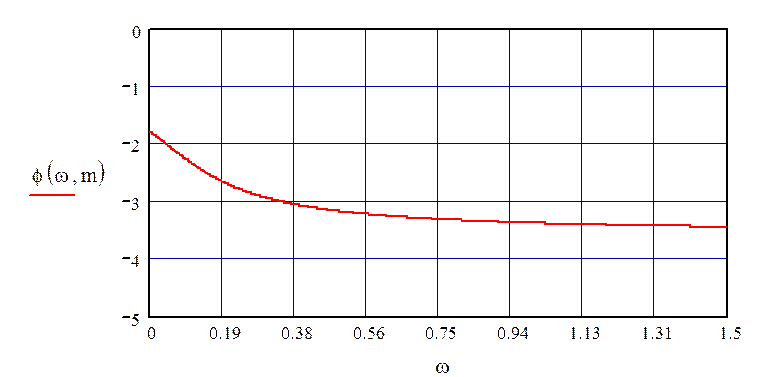
Рисунок 61 – РФЧХ объекта по каналу регулирования при τ=0
Согласно критерию Найквиста, годограф частотной характеристики устойчивой системы управления не должен охватывать точку с координатами (-1, j0), поэтому можно записать, что
Wpc(-mw+jw) = -1
Это критическое значение функции, когда система будет обладать заданной степенью колебательности.
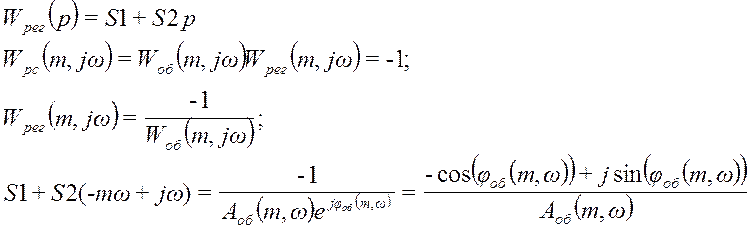
где Аоб(m,w) и jоб(m,w) – расширенные амплитудно-частотная и фазо-частотная характеристики.
Приравнивая вещественную и мнимую части выражения отдельно, находим настройки S1 и S2:
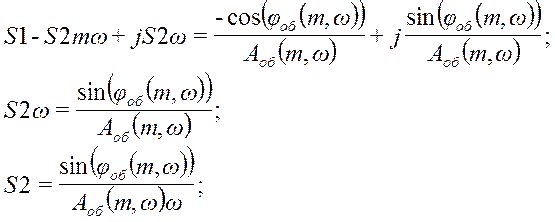
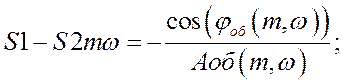
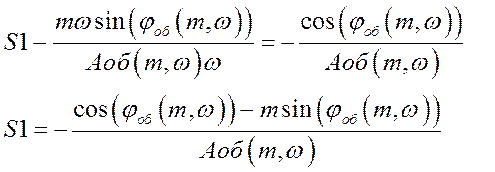
Данные построения АФХ разомкнутой системы представлены в таблице 10.3.
График АФХ представлен на рис. 62.
Таблица 10.3
|
S1 |
0 |
3.001 |
4.409 |
5.297 |
6.65 |
8.982 |
11.89 |
||
|
S2 |
0 |
0.509 |
0.905 |
1.227 |
1.75 |
2.478 |
3.52 |
||
|
ω |
0.5 |
0.75 |
0.9 |
1.0 |
1.15 |
1.3 |
1.5 |
|
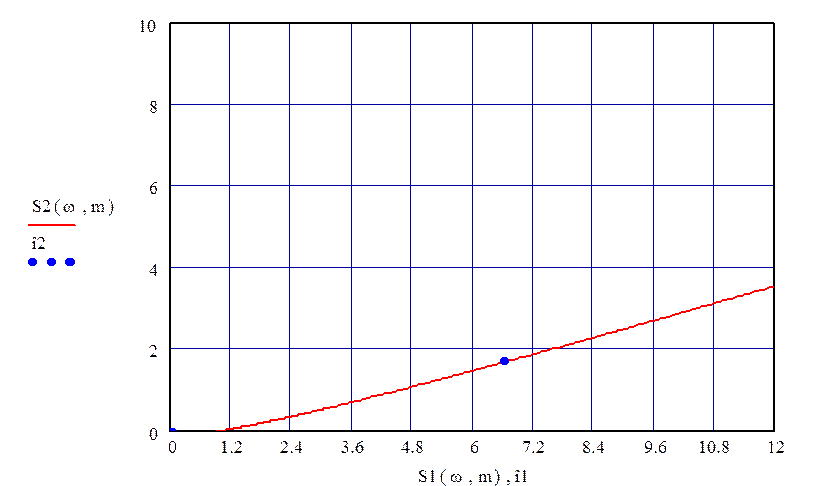
Рисунок 62. Кривая заданной степени колебательности m=0.221
Выбор пар настроек осуществляется в области положительных настроек регулятора в диапазоне частот до частоты среза объекта по каналу регулирования. Частота среза объекта равна ωср=1.5 с-1.
Первая пара настроек при частоте ωлев=1.0 с-1: S1=5,297
S2=1,227
Вторая пара настроек при частоте ωопт=1.15 с-1: S1=6,65
S2=1,75
Третья пара настроек при частоте ωправ=1.30 с-1: S1=8,982
S2=2,478
10.3 Расчет амплитудно-фазовой характеристики разомкнутой системы и определение запасов устойчивости по модулю и фазе
Передаточную функцию разомкнутой системы можно представить в виде произведения передаточных функций объекта и регулятора:
![]() ;
;
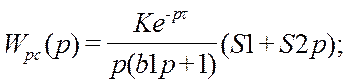
Для построения АФХ разомкнутой системы необходимо знать АФХ используемого регулятора. Поскольку мы рассчитываем систему с ПД – регулятором, то сначала рассчитаем его частотные характеристики.
![]() ;
;
![]() ;
;
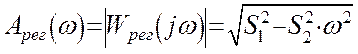 ;
;
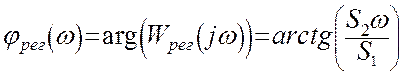 ;
;
Для получения вещественной и мнимой частотных характеристик надо числитель и знаменатель умножить на сопряженное знаменателю выражение:
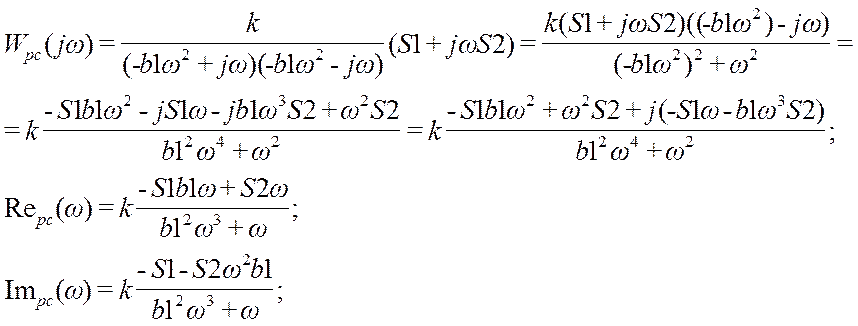
Используя полученные уравнения вещественной и мнимой частотных характеристик получим амплитудно-фазовую характеристику разомкнутой системы:
10.3.1 При настройках равных оптимальным АФХ будет иметь вид изображённый на рис. 63.
|

|

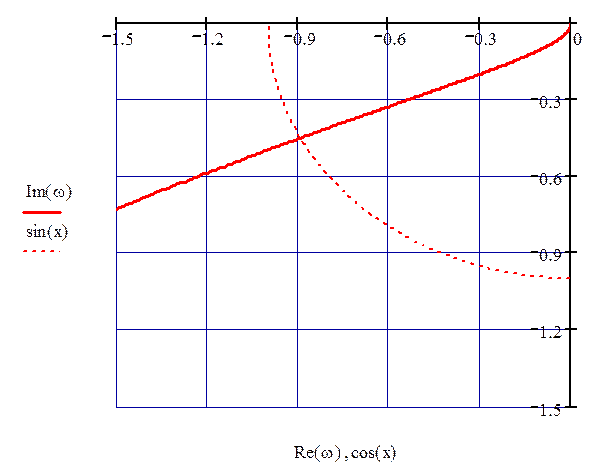
Рисунок 63 – АФХ разомкнутой системы при оптимальных настройках
В данном случае запасы устойчивости равны:
М =1; f = 28°.36'.
|
|

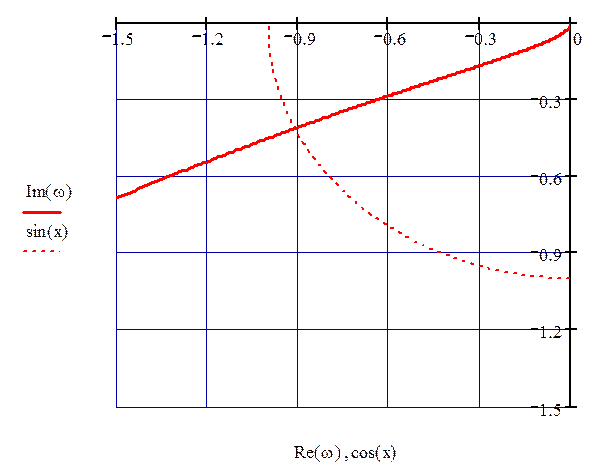
Рисунок 64 – АФХ разомкнутой системы при настройках левее оптимальных
В данном случае запасы устойчивости равны:
М =1; f = 25°.18'.
10.3.3 При настройках взятых правее оптимальных АФХ будет иметь вид, показанный на рис. 65.
|
|


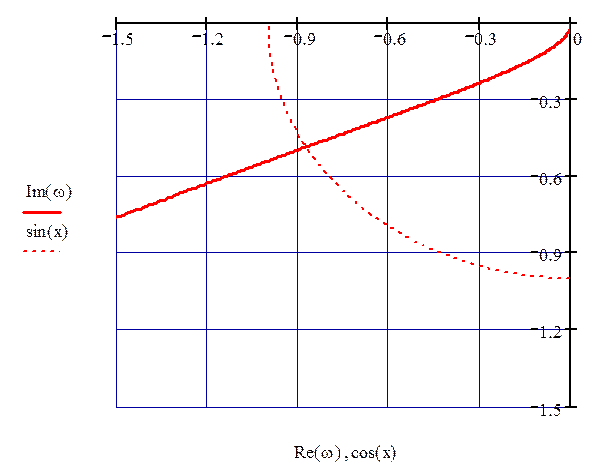
Рисунок 65 – АФХ разомкнутой системы при настройках правее оптимальных
В данном случае запасы устойчивости равны:
М =1; f = 30°.68'.
11. Расчет переходного процесса в замкнутой системе автоматического регулирования по каналу управления
Построение переходного процесса в замкнутой системе без запаздывания по каналу управления осуществляется по формуле:
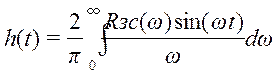 ;
;
Выведем аналитическое выражение и построим графики вещественной частотной характеристики.
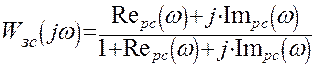 ;
;
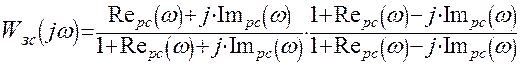 ;
;
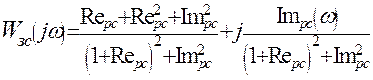 ;
;
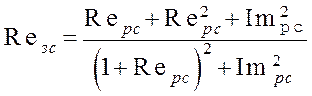 ;
;
где 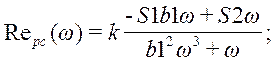
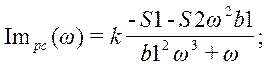
Построим в одних осях графики ВЧХ для настроек регулятора, взятых в оптимальной точке, левее и правее (рис. 66).

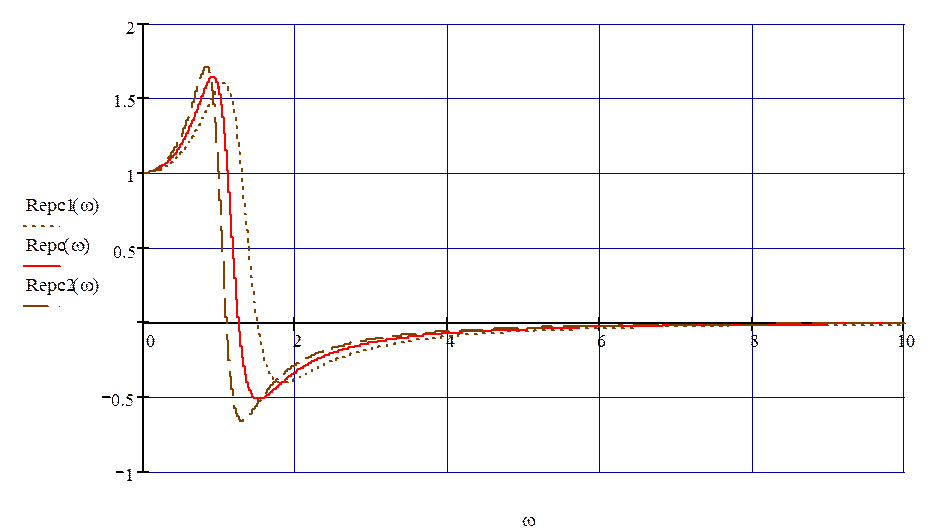
|
|
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.