С целью оценки влияния запаздывания по каналу управления при оптимальных настройках регулятора на характер переходного процесса в замкнутой системе, изобразим в одних координатных осях график с запаздыванием (плавная линия) и график без запаздывания (пунктирная линия) (рис. 50)
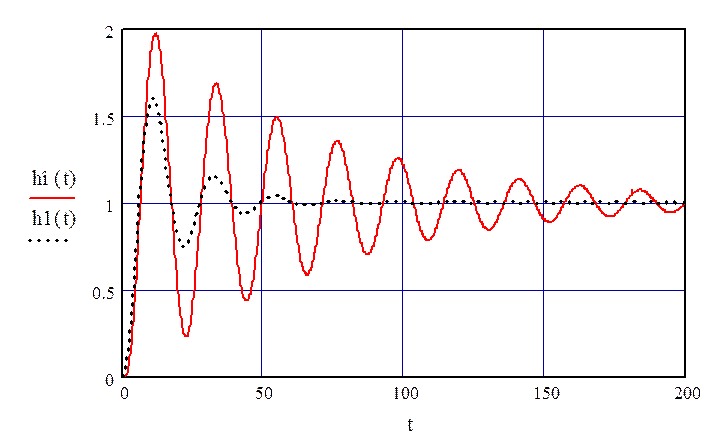
Рисунок 50 – переходный процесс по каналу управления при τ = 0 и τ = 1
Из данного графика видно, что при запаздывании переходный процесс по каналу регулирования имеет большое время регулирования, а также величину перерегулирования.Очевидно, что запаздывание в канале управления отрицательно влияет на параметры переходного процесса.
Можно проанализировать точность подбора оптимальных настроек регулятора в системе: для этого можно провести квадратичную интегральную оценку для каждого из вышеизложенных процессов.
Вычисляем её по формуле:
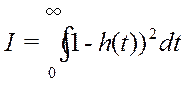
Для оптимальных настроек: 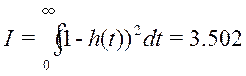 ;
;
Для настроек выбранных левее
оптимальных: 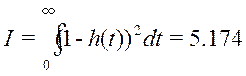 ;
;
Для настроек выбранных левее
оптимальных: 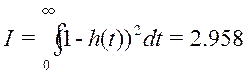 ;
;
Из приведённых расчётов видно, что наименьшую интегральную квадратичную оценку имеет процесс с настройками, взятыми правее оптимальных. Следовательно в дальнейшим расчетах за оптимальные настройки будем принимать S1=1.026, S2=0.005051.
|
|
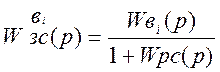
7.1 Первый канал возмущения
Передаточная функция по первому каналу возмущения имеет вид:
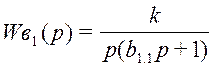 , где k = 0,5; b1.1
= 1;
, где k = 0,5; b1.1
= 1;
Передаточная функция замкнутой системы по первому каналу возмущения имеет вид:
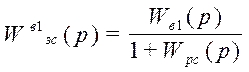 , где
, где 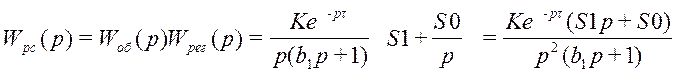 ;
;
Получим:
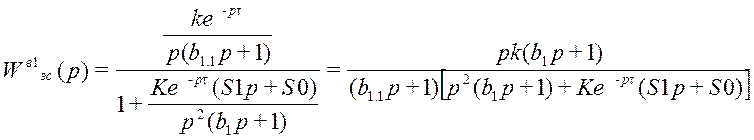 ;
;
S0 и S1 - оптимальные настройки ПИ-регулятора при t=0
S1=1.026, S2=0.005051, b1=5, K=1
В передаточной функции замкнутой системы заменим р на jw
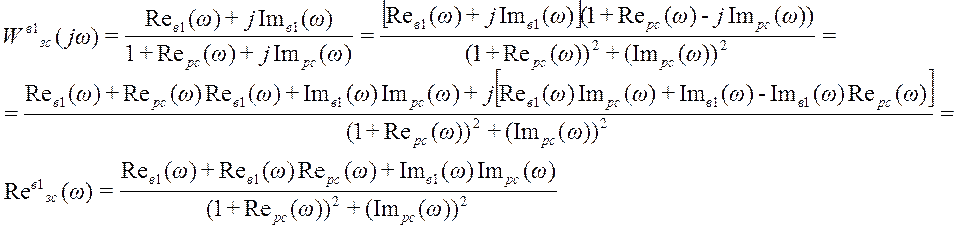 где
где
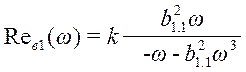 ;
;
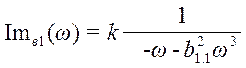 ;
;
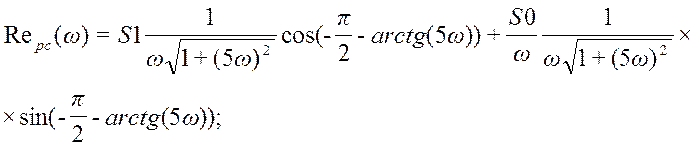
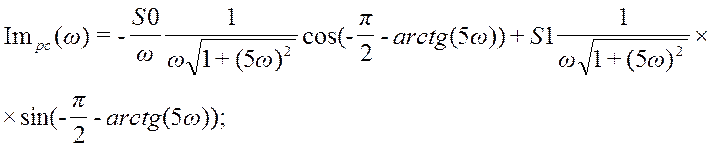
График для вещественной частотной характеристики замкнутой системы по первому каналу возмущения представлен на рис. 50.
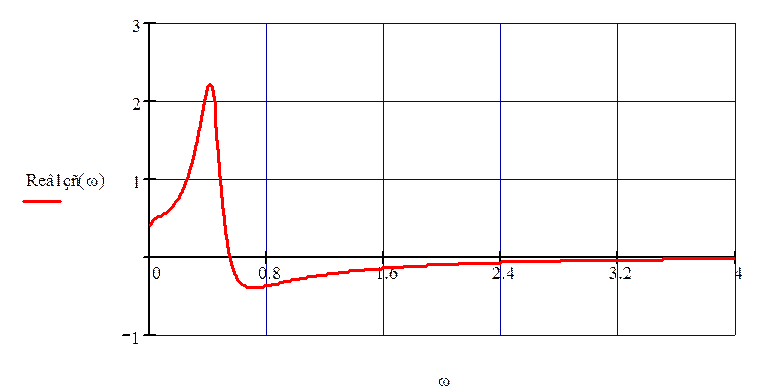
Рисунок 50 – ВЧХ по первому каналу возмущения
Рассчитаем переходный процесс по первому каналу возмущения с помощью следующего выражения:
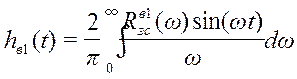 ;
;
Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 7.1
Таблица 7.1
|
t |
0 |
10 |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
|
h(t) |
0 |
0.216 |
0.585 |
0.371 |
0.356 |
0.324 |
0.295 |
0.266 |
0.24 |
Переходный процесс изображён на рис. 51.
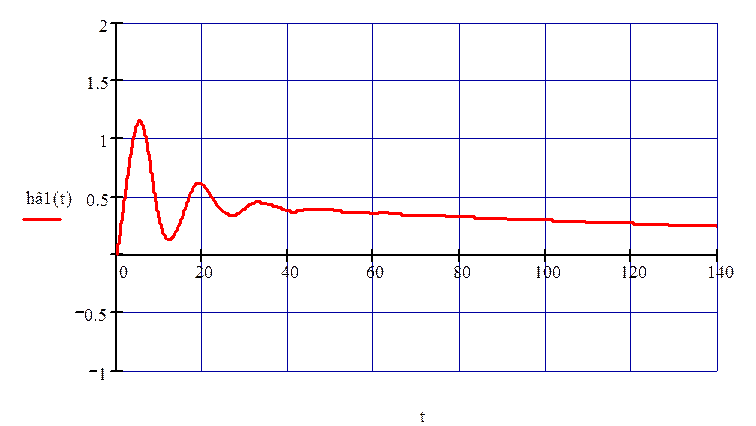
Рисунок 51 – Переходный процесс по первому каналу возмущения
7.2 Второй канал возмущения
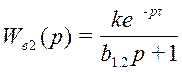 где
k = 0,5; b1.2 = 6; τ = 3
где
k = 0,5; b1.2 = 6; τ = 3
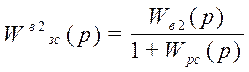
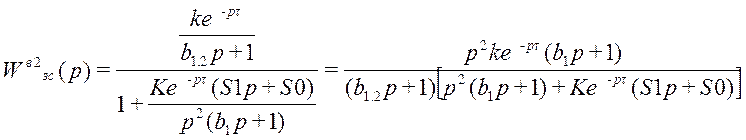
S0 и S1 - оптимальные настройки ПИ-регулятора при t=0
S1=1.026, S2=0.005051, b1=5, K=1;
Формула для вещественной частотной характеристики замкнутой системы по каналу возмущения выведена в предыдущем пункте и имеет вид:
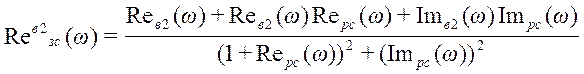 ,
где
,
где
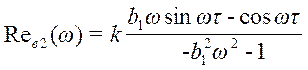 ;
;
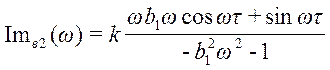 ;
;
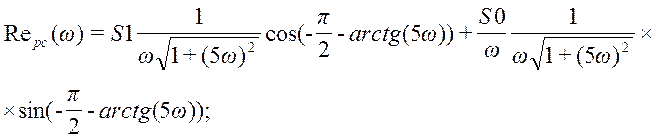
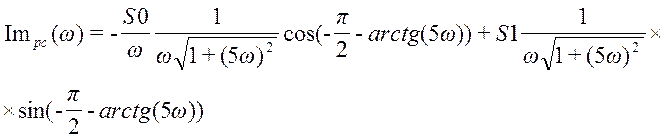
График ВЧХ замкнутой системы по второму каналу представлен на рис. 52.
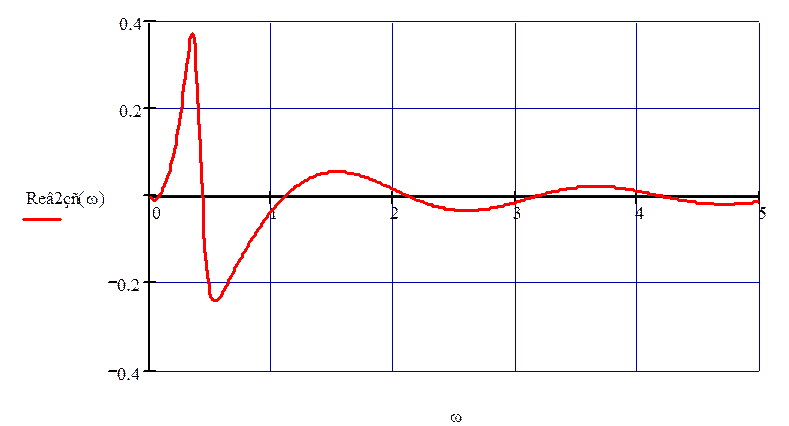
Рисунок 52 – ВЧХ по второму каналу возмущения
Рассчитаем переходный процесс по второму каналу возмущения с помощью следующего выражения:
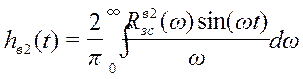 ;
;
Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 7.2
Таблица 7.2
|
t |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
40 |
60 |
|
h(t) |
0 |
0.116 |
0.01 |
-0.05 |
0.032 |
-0.008 |
-0.01 |
-0.004 |
0 |
Переходный процесс изображён на рис. 53.
|
|
Рисунок 53 – Переходный процесс по второму каналу возмущения при наличии(сплошная линия) и отсутствие запаздывания (пунутир).
7.3 Третий канал возмущения
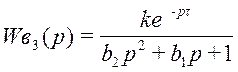 ,
где k = 0,5; b3.2 = 400;
b3.1 = 32; τ =
10;
,
где k = 0,5; b3.2 = 400;
b3.1 = 32; τ =
10;
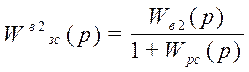 ;
;
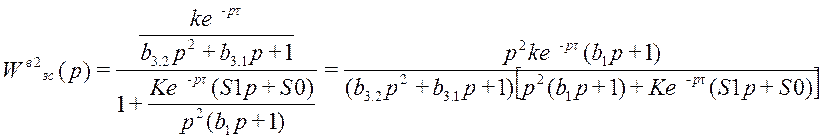 ;
;
S0 и S1 - оптимальные настройки ПИ-регулятора при t=0
S1=1.026, S2=0.005051, b1=5, K=1;
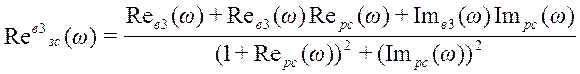 , где
, где
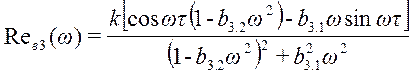 ;
;
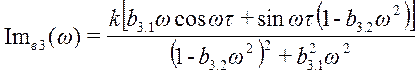 ;
;
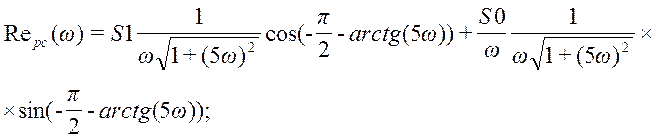
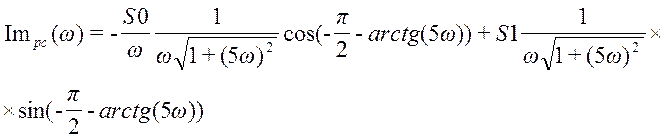
График ВЧХ замкнутой системы по третьему каналу возмущения изображён на рис. 54.
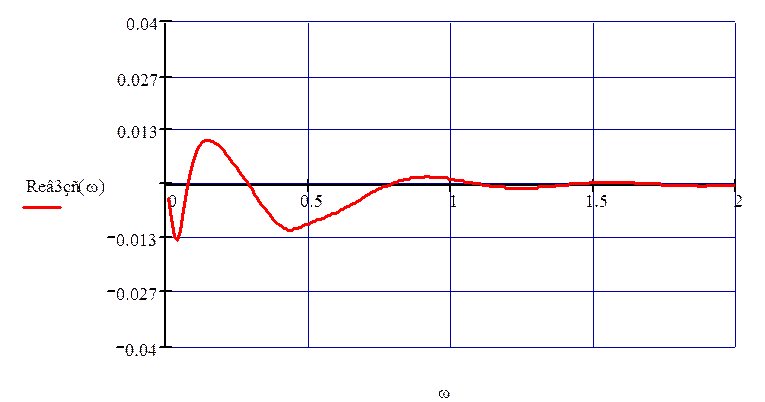
Рисунок 54 – ВЧХ по третьему каналу возмущения
Рассчитаем переходный процесс по второму каналу возмущения с помощью следующего выражения:
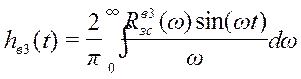 ;
;
Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 7.3
Таблица 7.3
|
t |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
80 |
100 |
|
h(t) |
0 |
0.004 |
-0.006 |
-0.01 |
-0.01 |
-0.009 |
-0.007 |
-0.003 |
-0.002 |
Переходный процесс по третьему каналу возмущения при отсутствии запаздывания по каналу управления представлен на рис. 55.
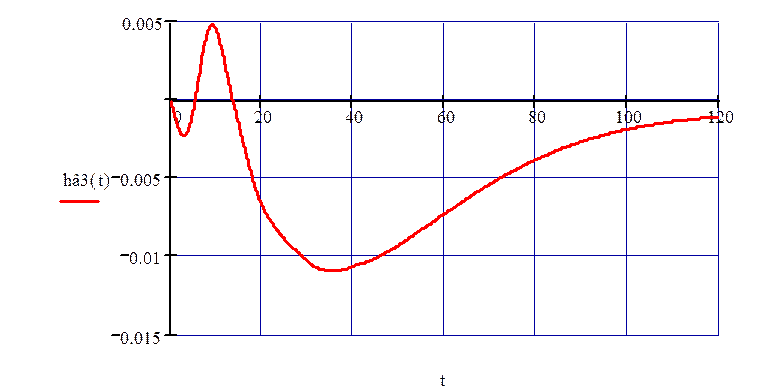
Рисунок 55 – Переходный процесс по третьему каналу возмущения
8 Определение нулей и полюсов передаточных функций замкнутой системы.
Для получения корневых показателей качества системы управления необходимо рассчитать корни полиномов числителя и знаменателя передаточной функции замкнутой системы для случаев, когда запаздывание в канале регулирования равно нулю. Для этого необходимо в общие функции замкнутой системы подставить конкретные выражения передаточных функций объекта и регулятора и привести Wзс(p) к отношению произведений полиномов.
Определение полюсов передаточной функции необходимо производить для каждого сомножителя характеристического полинома отдельно.
8.1 Канал управления
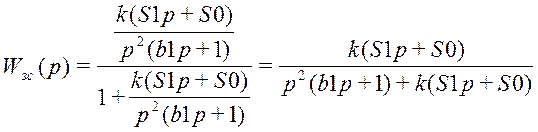
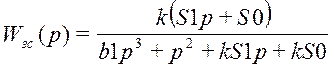
Нули передаточной функции:
![]()
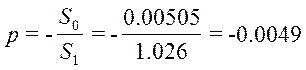
Полюса передаточной функции:
Два комплексных сопряженных полюса известны:
![]()
![]()
где ![]() , а m=0.221;
, а m=0.221;
![]() ;
;
![]() ;
;
Оставшийся действительный полюс находится путем решения уравнения:
![]()
В
результате решения этого уравнения получим: ![]()
Изобразим на комплексной плоскости полюса и нули передаточной функции
(рис. 56)
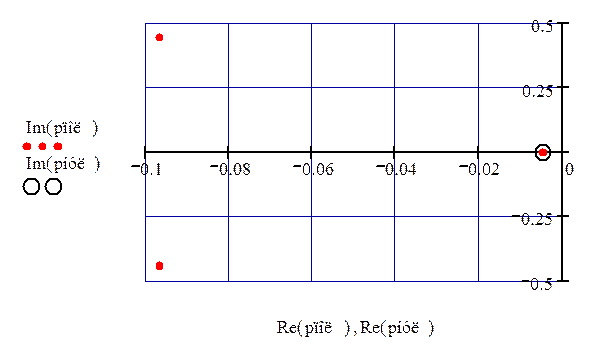
Рисунок – 56 нули и полюса канала управления.
8.2 Первый канал возмущения
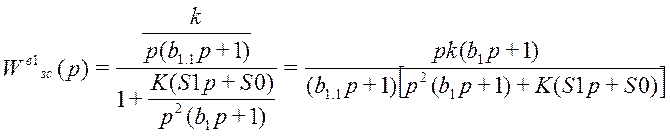 ;
;
где k = 0,5; b1.1 = 1; S0=0.00505, S1=1.026, b1=5, K=1;
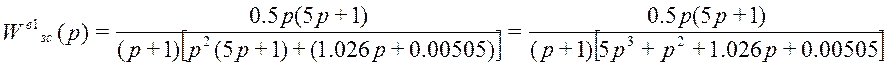 ;
;
Нули передаточной функции:
![]()
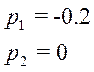
Полюса передаточной функции:
Решая
уравнение ![]() , найдем
, найдем
![]()
Решая
уравнение ![]() , найдем
, найдем
![]() ;
;
![]() ;
;
![]()
Изобразим на комплексной плоскости полюса и нули передаточной функции
(рис. 57)
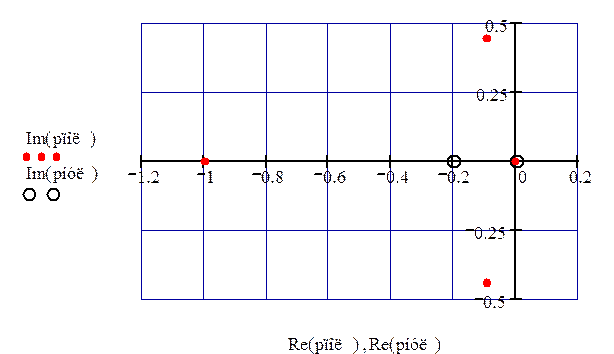
Рисунок – 57 нули и полюса первого канала возмущения
8.3 Второй канал возмущения
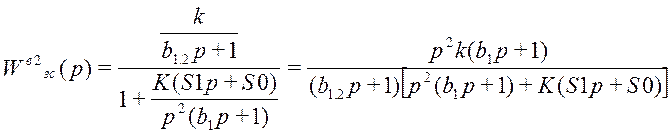 ;
;
где k = 0,5; b1.2 = 6; S0=0.00505, S1=1.026, b1=5, K=1;
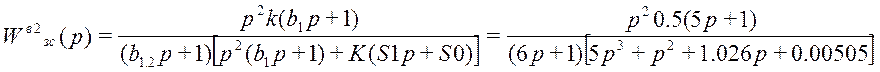
Нули передаточной функции:
![]()
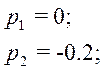
Полюса передаточной функции:
Решая
уравнение, ![]() найдем
найдем
![]()
Решая
уравнение ![]() , найдем
, найдем
![]() ;
;
![]() ;
;
![]()
Изобразим на комплексной плоскости полюса и нули передаточной функции
(рис. 58)
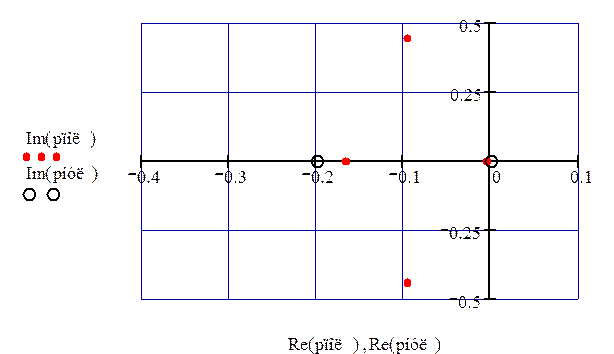
Рисунок – 58 нули и полюса второго канала возмущения
8.4 Третий канал возмущения
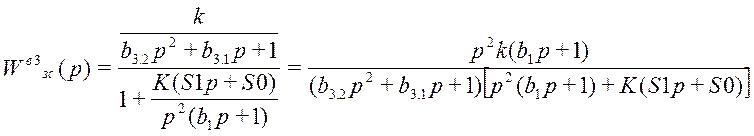 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.