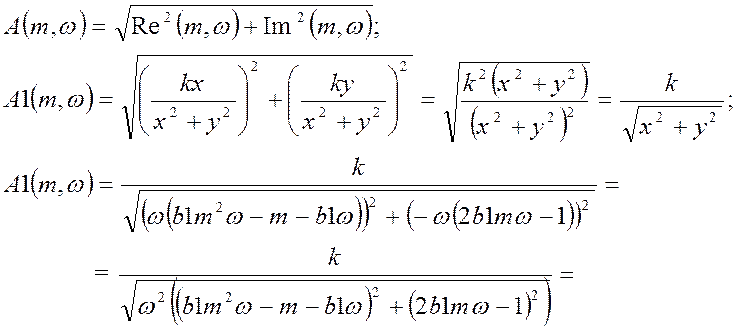
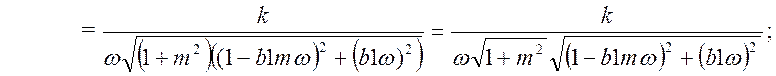
Фазо-частотная характеристика
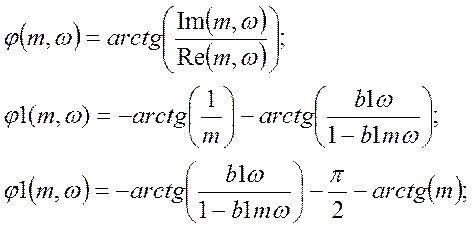
Для второго динамического звена:
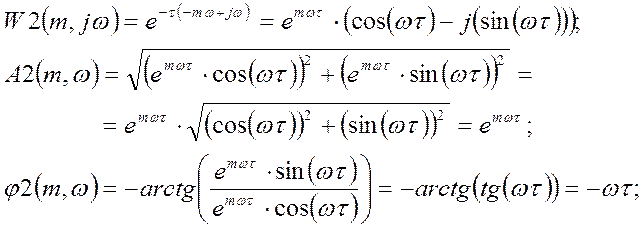
Построим расширенные частотные характеристики объекта по каналу регулирования для m=0.221, τ =1:
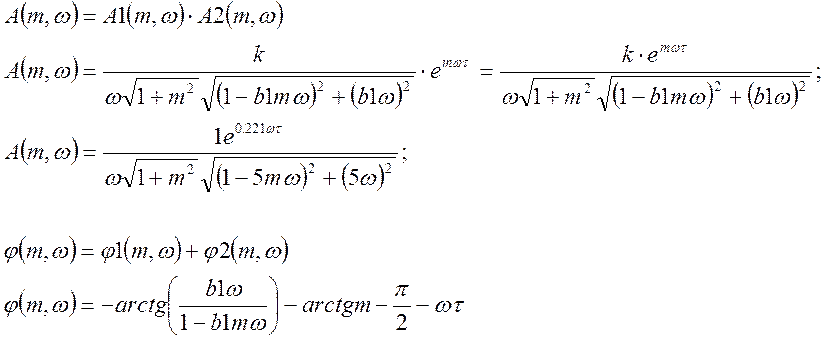 |
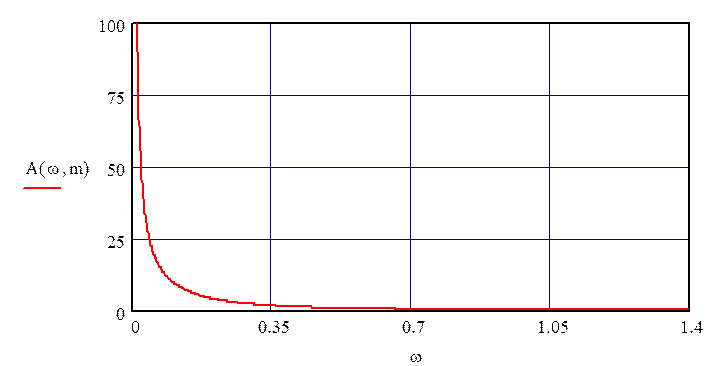
Рисунок 18 – РАЧХ по каналу управления
Данные для построения РАЧХ приведены в таблице 2.1.
Таблица 2.1
|
ω |
0.01 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
1.4 |
|
А(m,ω) |
98.8 |
4.03 |
1.27 |
0.617 |
0.36 |
0.24 |
0.18 |
0.13 |
Для обеспечения непрерывности фазо-частотной характеристики после точки разрыва 1/b1m=0,905, прибавляем период -p.
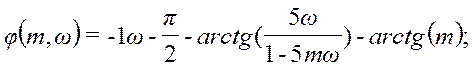 при
ω < 0,905
при
ω < 0,905
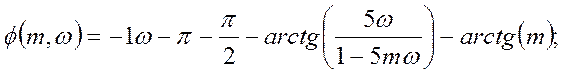 при
ω ≥ 0,905
при
ω ≥ 0,905
Данные для построения РАЧХ приведены в таблице 2.2.
Таблица 2.2
|
ω |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
1.2 |
1.4 |
|
j(m,ω) |
-1.79 |
-2.89 |
-3.49 |
-3.86 |
-4.13 |
-4.38 |
-4.61 |
-4.84 |
График полученной РФЧХ имеет следующий вид (рис. 19)
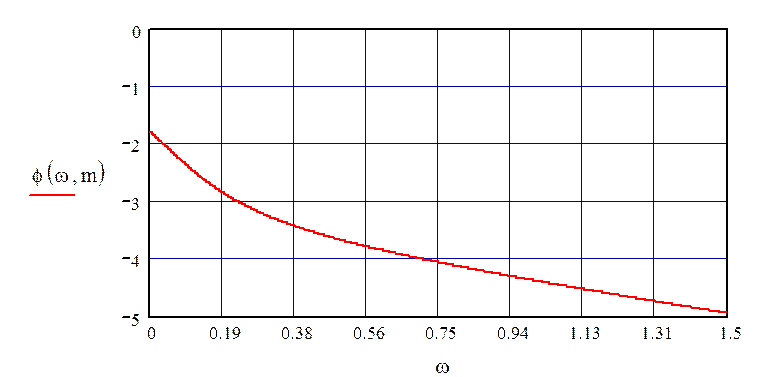
Рисунок 19 – РФЧХ по каналу управления
2.2. Расчет и построение кривой с заданной степенью колебательности в плоскости настроек ПИ-регулятора(S0-S1)
Выведем формулу для расчета настроек ПИ-регулятора – S0 и S1:
Согласно критерию Найквиста, годограф частотной характеристики устойчивой системы управления не должен охватывать точку с координатами
(-1,j0), поэтому можно записать, что
Wpc(-mw+jw) = -1
Это критическое значение функции. Найдем настройки ПИ-регулятора
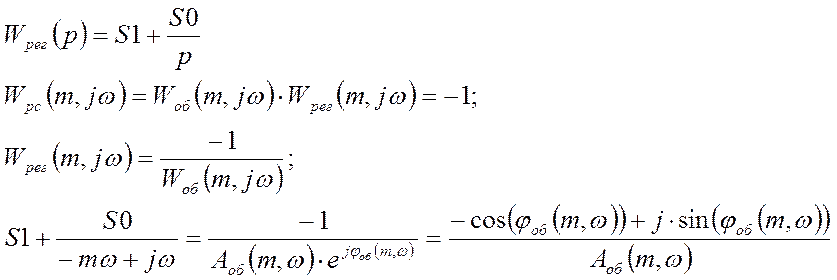
где Аоб(m,w) и jоб(m,w) – расширенные амплитудно-частотная и фазо-частотная характеристики.
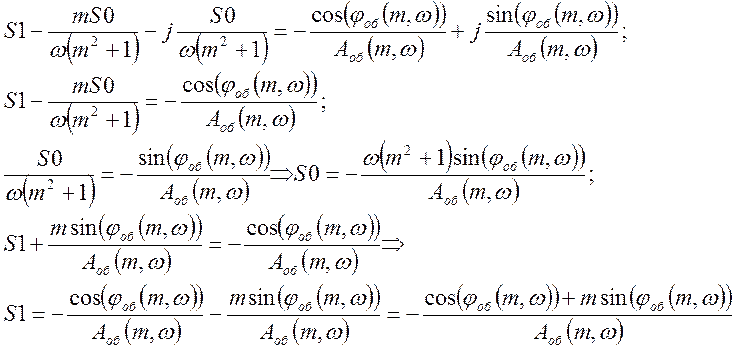 |
Данные для построения плоскости настроек ПИ-регулятора представлены в таблице 2.3.
Таблица 2.3
|
S0 |
0 |
0.002 |
0.005 |
0.009 |
0.012 |
0.013 |
0.008 |
0 |
||
|
S1 |
0 |
0.031 |
0.064 |
0.114 |
0.17 |
0.213 |
0.329 |
0.39 |
||
|
ω |
0 |
0.04 |
0.08 |
0.12 |
0.16 |
0.2 |
0.24 |
0.27 |
Плоскость настроек ПИ-регулятора при τ = 1 имеет вид, представленный на рис. 20.
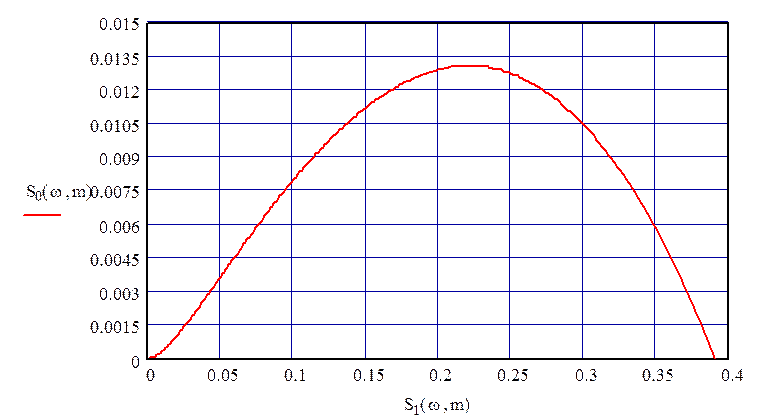
Рисунок 20 – Плоскость настроек S0-S1(τ =1)
2.3 Определение оптимальных настроек ПИ-регулятора при τ =1
Оптимальные настройки ПИ-регулятора, обеспечивающие при заданной степени колебательности m минимизацию квадратичной интегральной оценки J2 переходного процесса в замкнутой системе, определяются, как координаты точки, лежащей на правой ветви кривой S0-S1 вблизи её вершины. Найти положение этой точки можно при помощи следующего равенства:
![]()
Из графика видно, что wmax соответствует точка с координатами: S0=0.013 S1=0.23
Частота wmax=0.17
wопт=1.3×0.17=0.221
Подставляя найденное значение wопт=0.221 и m=0.221 находим:
S0опт = S0(m,wопт) = 0.011
S1опт = S1(m,wопт) = 0.295
2.4 Построение амплитудно-фазовой характеристики разомкнутой системы определение запасов устойчивости по модулю и по фазе
Передаточная функция разомкнутой системы
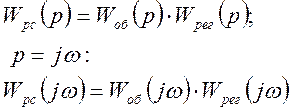
Для построения АФХ разомкнутой системы найдём вещественную и мнимую части:
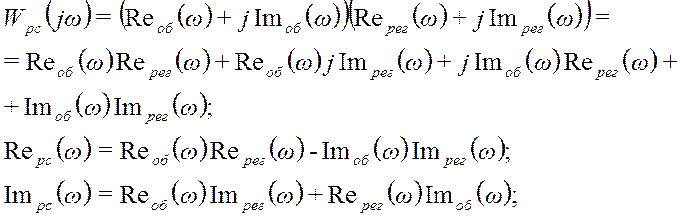
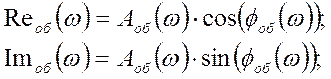
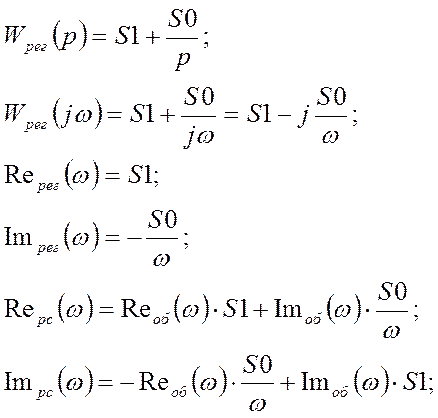
Построим АФХ разомкнутой системы при τ =1:
По выведенным амплитудно-частотной и фазо-частотной характеристикам и найденным настройкам регулятора S0 и S1 получим:
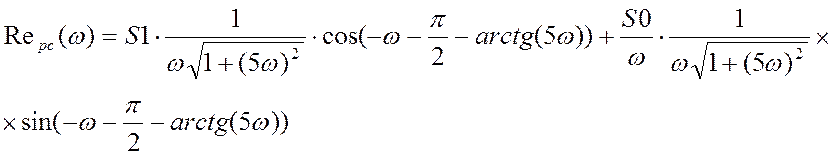
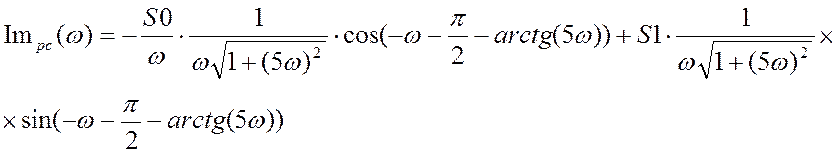
Где: ![]() ,
,
![]()
Данные построения АФХ разомкнутой системы представлены в таблице 2.4.
Таблица 2.4.
|
Re |
-111.43 |
-5.748 |
-4.369 |
-3.519 |
-2.546 |
-2.241 |
-0.977 |
||
|
Im |
-22.82 |
-4.236 |
-3.414 |
-2.815 |
-1.997 |
-1.705 |
-0.414 |
||
|
ω |
0.01 |
0.05 |
0.06 |
0.07 |
0.09 |
0.1 |
0.2 |
По приведённым данным строим АФХ разомкнутой системы (рис. 21).
|

|

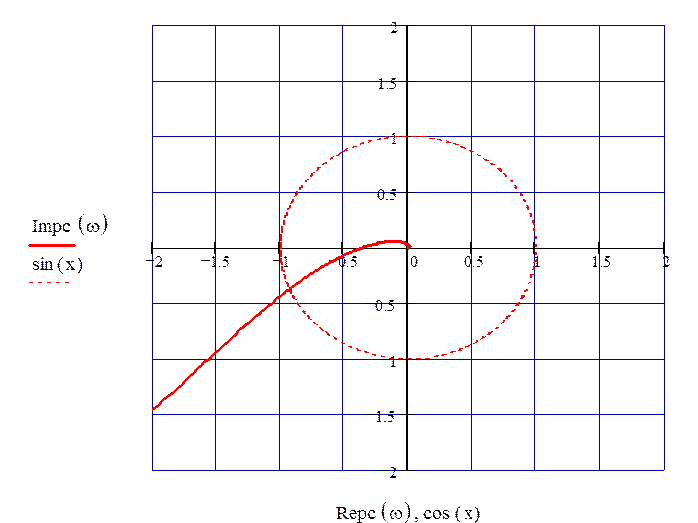
Рисунок 21 – АФХ разомкнутой системы при τ =1
Запас устойчивости по модулю М определяется как расстояние от годографа амплитудно-фазовой характеристики при Im(Wрс(jw))=0 до точки с координатами (-1;j0).
М = |-1 - (-0.4)| = 0.6
Запас устойчивости по фазе определяется как угол между отрицательным направлением оси Re и вектором Wрс(jw) единичной длины:
f = 21°.1’
3.1 Построение переходных процессов при τ = 1
3.1 Построение переходного процесса в замкнутой системе по каналу управления.
Общая формула передаточной функции замкнутой системы:
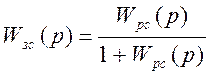 ;
;
где
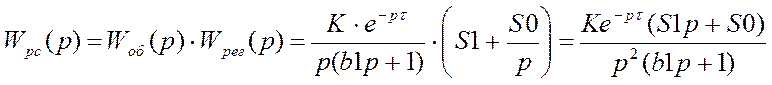 ;
;
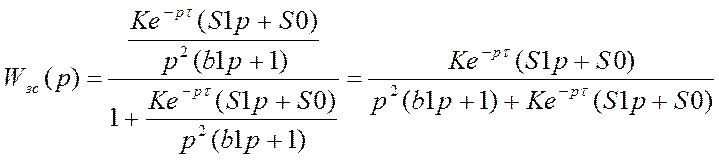
Где S0 = 0.011 S1= 0.295 (при τ = 1).
Определяем аналитическое
выражение для расчета вещественной частотной характеристики замкнутой системы ![]() :
:
В передаточной функции замкнутой системы заменим р на jw
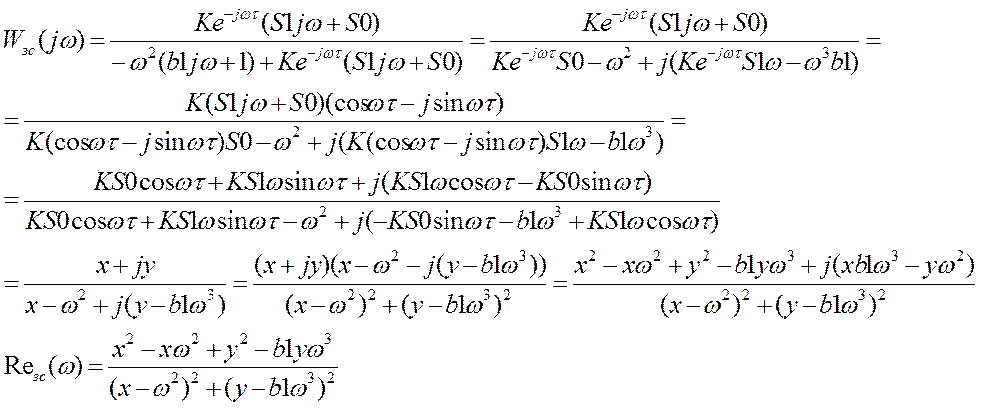 Где
Где
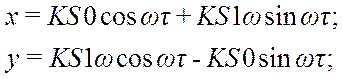
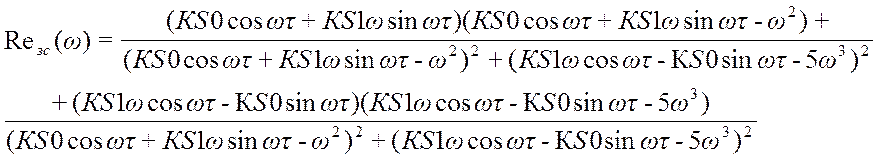
Подставляя исходные данные получим:
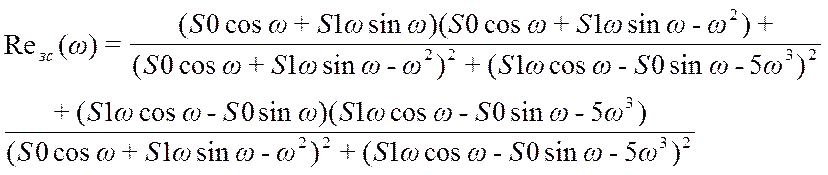
Подставляя в формулу для ВЧХ по каналу управления оптимальные настройки регулятора S0 = 0.011, S1= 0.295 строим график ВЧХ при наличии запаздывания в канале управления при τ =1.
Для построения переходного процесса воспользуемся методом, который основан на использовании вещественной частотной характеристики замкнутой системы – метод трапеций.
Представим ВЧХ замкнутой системы в виде непрерывной ломаной линии.
Действуя по алгоритму данного метода, заменяем ломаную линию комбинацией трапеций. Вещественная частотная характеристика системы определяется как сумма ординат всех трапеций:
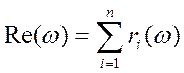 , где
, где
ri – высота i- номер трапеции.
Переходный процесс в системе находится как сумма переходных процессов для каждой из трапеций:
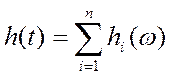 где
где 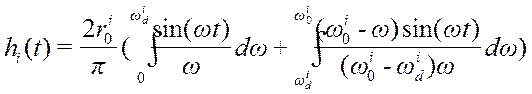 ;
;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.