|
ω |
0 |
0.25 |
0.5 |
0.75 |
1.0 |
1.25 |
1.5 |
1.75 |
2.0 |
|
А(ω) |
0.5 |
0.278 |
0.158 |
0.108 |
0.082 |
0.066 |
0.055 |
0.047 |
0.042 |
График АЧХ по второму каналу возмущения представлен на рис. 11.
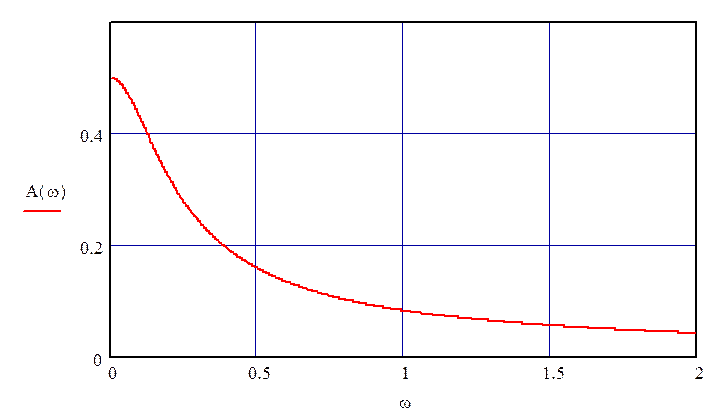
Рисунок 11 – АЧХ по второму каналу возмущения.
1.3.3 Построение фазо-частотной характеристики.
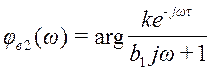 =
=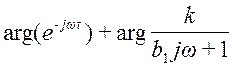 =
=![]()
Подставляя исходные данные ( b1=6; τ=3)получим:
![]() ;
;
Данные построения ФЧХ канала возмущения 2 представлены в таблице 1.11.
Таблица 1.11.
|
ω |
0 |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
|
j(ω) |
0 |
-2.72 |
-4.37 |
-5.98 |
-7.46 |
-9.02 |
-10.5 |
-12.05 |
-13.48 |
График ФЧХ по второму каналу возмущения представлен на рис.12.
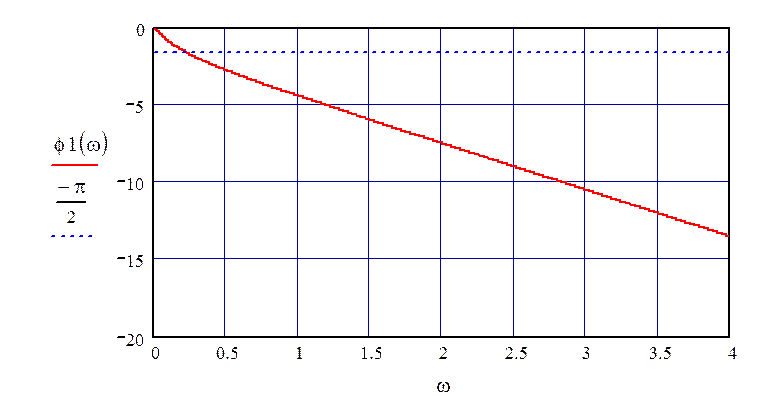
Рисунок 12 – ФЧХ по второму каналу возмущения.
1.3.4 Амплитудо-фазовая характеристика.
Для получения АФХ необходимо получить выражения для вещественной и мнимой составляющих Wоб(jw):
![]() ;
;
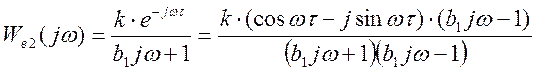 ;
;
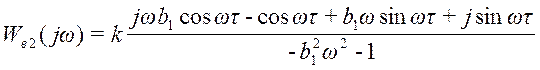 ;
;
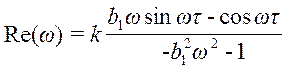 ;
;
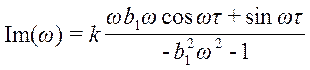 ;
;
Для получения амплитудно-фазовой характеристики воспользуемся формулами:
![]() ;
;
![]() ;
;
![]() ;
;![]()
![]() ;
;
Данные построения АФХ канала возмущения 2 представлены в таблице 1.12.
Таблица 1.12.
|
Re |
-0.487 |
-0.433 |
0.286 |
003 |
-0.146 |
-0.083 |
-0.025 |
|
Im |
-0.045 |
-0.205 |
-0.319 |
-0.319 |
-0.06 |
-0.06 |
0.078 |
|
ω |
0.01 |
0.05 |
0.1 |
0.2 |
0.5 |
0.8 |
1 |
График АФХ по второму каналу возмущения представлен на рис. 13.
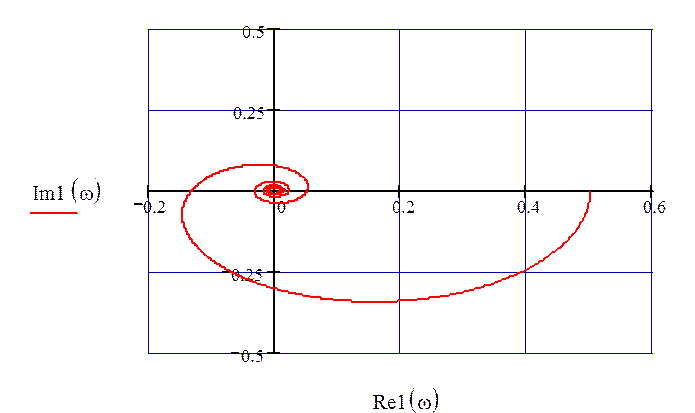
Рисунок 13 – АФХ по второму каналу возмущения.
1.4Третий канал возмущения
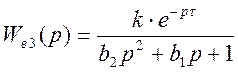 ;
;
1.4.1 Построение переходного процесса:
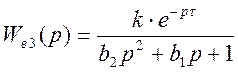 ;
;
![]() <
<![]() ;
;
![]() <
<![]() ;
;
Следовательно, имеем передаточную функцию колебательного звена:
Перепишем функцию в виде:
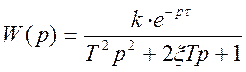 где
где ![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Разложим характеристический полином на множители:
![]()
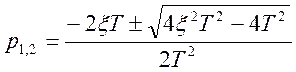 ;
;
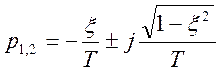 ;
;
![]() где
где 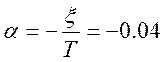 ,
, 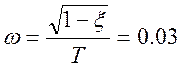 ;
;
Переходную функцию получаем при ступенчатом входном воздействии без учета чистого транспортного запаздывания, которое учтем в окончательной формуле:
![]() ;
;
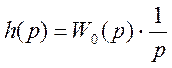 ;
;
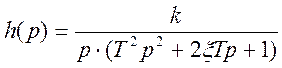 ;
;
Разлагаем изображение на простые дроби:
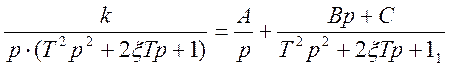 ;
;
Найдём неизвестные коэффициенты разложения:
![]()
При ![]() :
:
![]()
При ![]() :
:
![]()
При ![]() :
:
![]()
Тогда: ![]() ;
; ![]() ;
;
![]() ;
;
Следовательно:
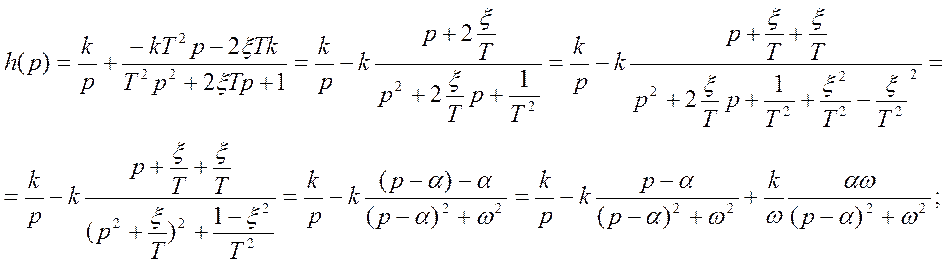
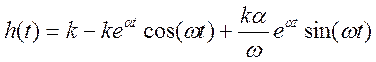 ;
;
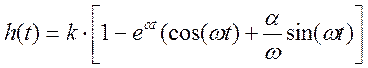 ;
;
Учитывая запаздывание получаем:
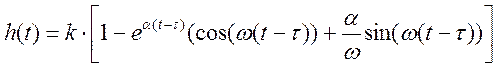 ;
;
Упростим выражние:
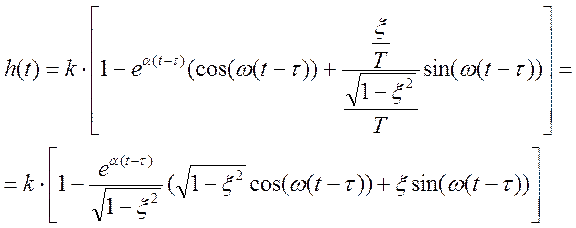
Примем
![]() , тогда:
, тогда: ![]()
Следовательно:
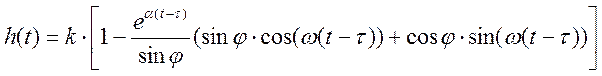 ;
;
Окончательная формула имеет вид:
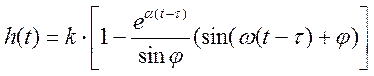 ;
;
где
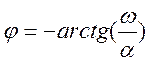 ;
;
Подставляя k=0,5; b2=400; b1=32; τ=10, получаем переходную функцию по третьему каналу возмущения.
Данные для построения переходного процесса по третьему каналу возмущения представлены в таблице 1.13.
Таблица 1.13
|
t |
10 |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
|
h(t) |
0 |
0.336 |
0.468 |
0.504 |
0.507 |
0.503 |
0.0501 |
0.499 |
График переходной функции по второму каналу возмущения представлена на рис. 14.
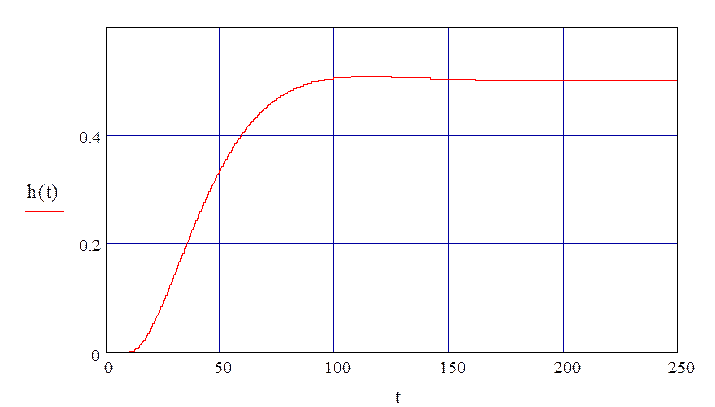
Рисунок 14 – Переходная функция по третьему каналу возмущения.
1.4.2 Построение амплитудо-частотной характеристики:
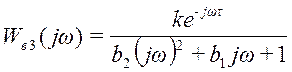 ;
;
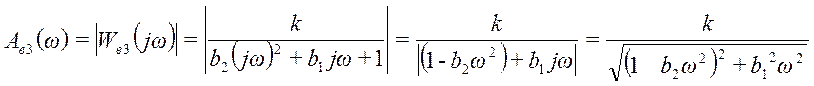 ;
;
Подставляя исходные данные (k=0,5; b2=400; b1=32; τ=10) получим:
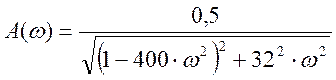 ;
;
Данные построения АЧХ канала возмущения 3 представлены в таблице 1.14.
Таблица 1.14.
|
ω |
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1.0 |
|
А(ω) |
0.5 |
0.03 |
0.007 |
0.003 |
0.002 |
0.001 |
График АЧХ по третьему каналу возмущения представлен на рис. 15.
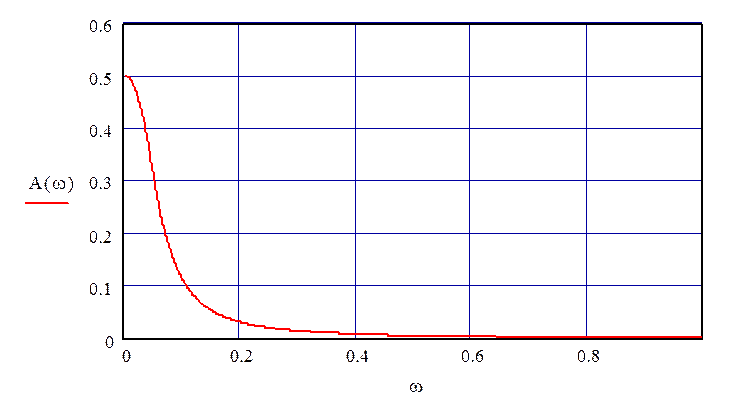
Рисунок 15 – АЧХ по третьему каналу возмущения.
1.4.3 Построение фазо-частотной характеристики.
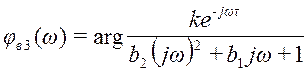 =
=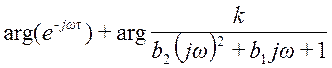 ;
;
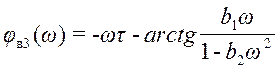 при ω<
при ω<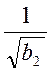 ;
;
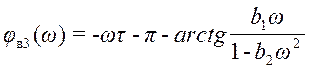 при ω≥
при ω≥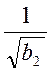 ;
;
Подставляя исходные данные ( b1=32; b2=400; τ=100)получим:
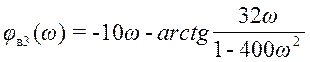 при ω≤0,05
при ω≤0,05
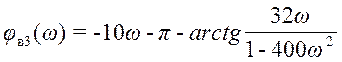 при ω≥0,05
при ω≥0,05
Данные построения ФЧХ канала возмущения 3 представлены в таблице 1.15.
Таблица 1.15.
|
ω |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
|
j(ω) |
0 |
-3.14 |
-4.67 |
-5.83 |
-6.94 |
-7.99 |
-9.0 |
-10.04 |
-11.52 |
График ФЧХ по третьему каналу возмущения представлен на рис. 16.
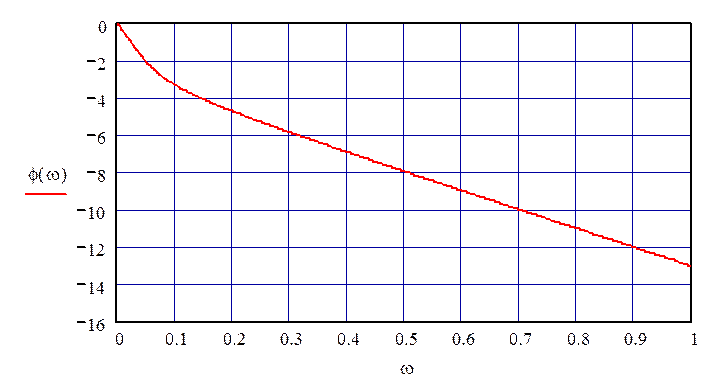
Рисунок 16 – ФЧХ по третьему каналу возмущения.
1.4.4 Амплитудо-фазовая характеристика.
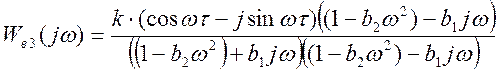
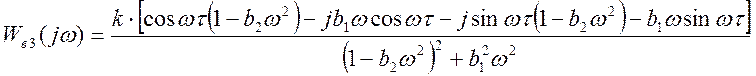
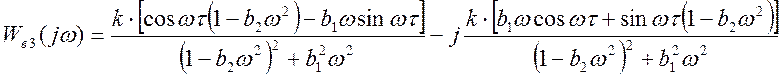
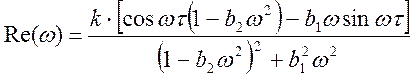 ;
; 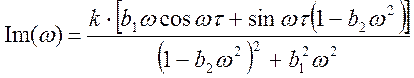 ;
;
Для получения амплитудно-фазовой характеристики воспользуемся формулами:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Данные построения АФХ канала возмущения 3 представлены в таблице 1.16.
Таблица 1.16.
|
Re |
0.451 |
-0.15 |
-0.187 |
-0.183 |
-0.137 |
0.112 |
0.008 |
||
|
Im |
-0.202 |
-0.274 |
-0.172 |
-0.092 |
-0.001 |
0.221 |
-0.031 |
||
|
ω |
0.01 |
0.05 |
0.06 |
0.07 |
0.09 |
0.1 |
0.2 |
График АФХ по третьему каналу возмущения представлен на рис. 17.
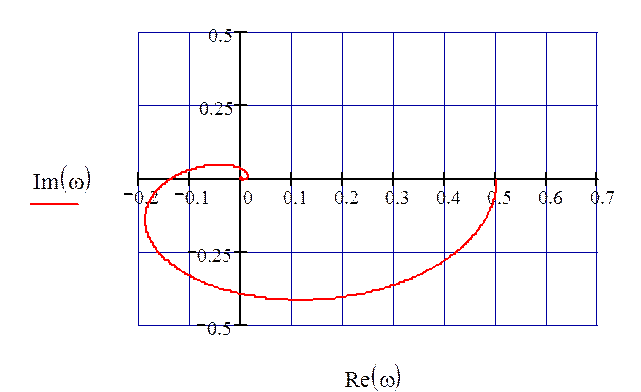
Рисунок 17 – АФХ по третьему каналу возмущения.
2. Синтез замкнутой САУ с ПИ-регулятором при τ = 1
Синтез замкнутой САУ с ПИ-регулятором проводиться методом расширенных частотных характеристик для объекта с передаточной функцией по каналу регулирования.
Передаточная функция по каналу регулирования имеет вид:
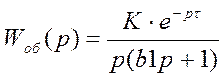
2.1 Построение графиков расширенных амплитудно-частотной и фазо-частотной характеристик
Для определения расширенных частотных характеристик объекта по каналу регулирования в передаточную функцию сделаем подстановку:
![]() ,
,
где m - заданная степень колебательности системы , m=0.221
w - частота (0≤w≤∞)
Разобьём передаточную функцию на типовые динамические звенья:
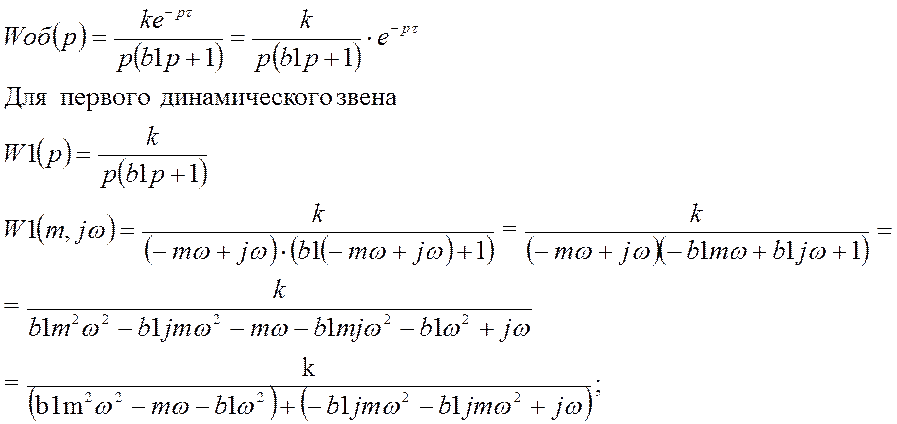
Полученное РАФХ представим в виде:
![]()
Примем:
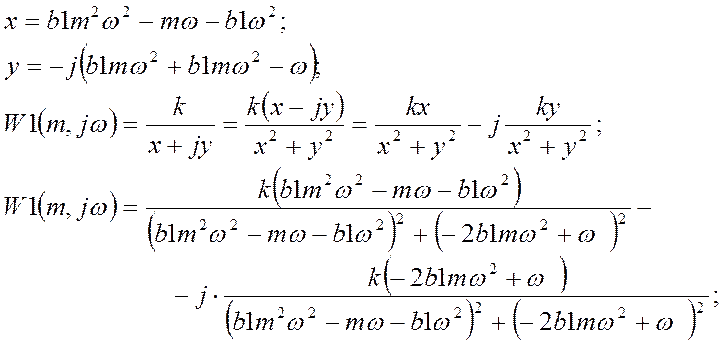
Получили:
![]() =
=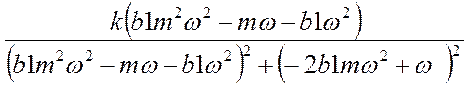
![]() =
=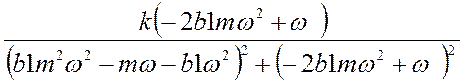
Выведем уравнение амплитудно-частотной характеристики
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.