Анализ и синтез одноконтурных систем автоматического управления (САУ), страница 10

Рисунок 66  –  Вещественные частотные характеристики ЗСАУ при оптимальных настройках, настройках взятых правее и левее оптимальных

Построим переходные процессы в одних осях для настроек регулятора, взятых в оптимальной точке, левее и правее (рис. 67).

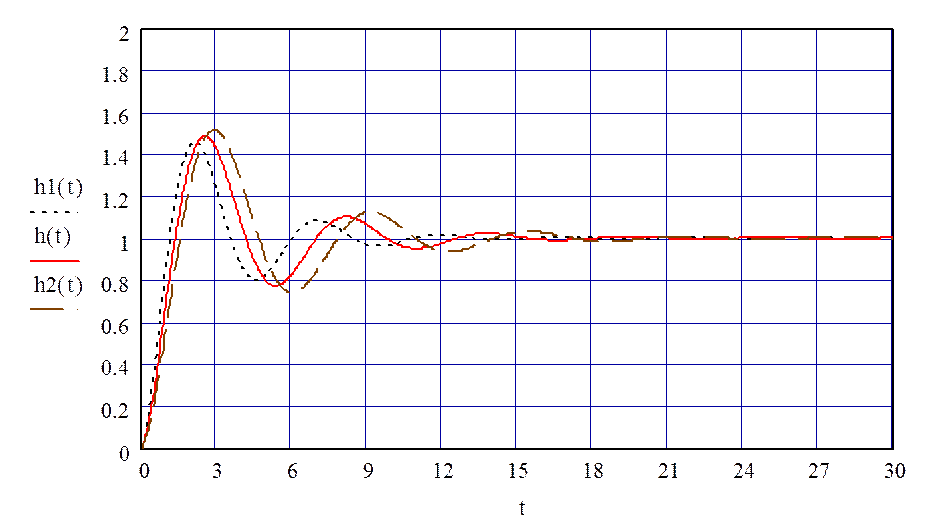
Рисунок 67 –  Переходный процесс замкнутой системы с тремя парами настроек при t=0

Данные для построения переходных процессов при оптимальных настройках регулятора, настройках взятых правее и левее оптимальных,  представлены в сводной таблице 11.1.

Таблица 11.1 

Оптимальные настройки
ω	0	2	4	6	8	10	12	14	16	18	20
h2	0	1.38	1.05	0.83	1.11	0.98	0.89	1.02	1.0	1.0	1.0
Настройки, взятые левее оптимальных
ω	0	2	4	6	8	10	12	14	16	18	20
h3	0	1.46	1.25	0.74	1.03	1.08	1.17	1.00	1.02	1.0	1.0
Настройки, взятые правее оптимальных
ω	0	2	4	6	8	10	12	14	16	18	20
h4	0	1.27	0.87	0.99	1.03	0.99	1.01	1.0	1.0	0.99	1.0

Далее определим показатели качества для переходного процесса без запаздывания с оптимальными настройками регулятора

Время переходного процесса   Т = 9,2 с

Величина перерегулирования   σ = 49 %

Собственная частота системы   ω = 0,108

Определим показатели качества для переходного процесса без запаздывания с настройками регулятора взятыми левее оптимальных.

Время переходного процесса   T = 10,5 с

Величина перерегулирования   σ = 51 %

Собственная частота системы   ω = 0,095,5имальнами з запаздывания со е оптимальных.

Определим показатели качества для переходного процесса без запаздывания с настройками регулятора взятыми правее оптимальных.

Время переходного процесса   T = 8,1 с

Величина перерегулирования   σ = 45 %

Собственная частота системы   ω = 0,123

Можно проанализировать подбор настроек регулятора в системе: для этого необходимо провести квадратичную интегральную оценку для каждого из вышеизложенных процессов.

Вычисляем её по формуле:

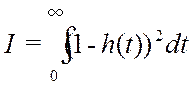
Для оптимальных настроек: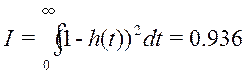

Для настроек взятых левые: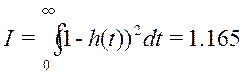  

Для настроек взятых правые: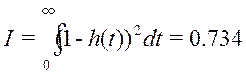

Из приведённых расчётов видно, что наименьшую интегральную квадратичную оценку имеет процесс с настройками, взятыми правее оптимальных. Следовательно в дальнейшим расчетах за оптимальные настройки будем принимать  S1=8.982, S2=2.478.

12. Расчет переходного процесса в замкнутой системе автоматического регулирования по каналам возмущения

12.1  Первый канал возмущения

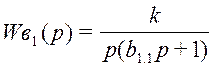 , где k = 0,5; b_1.1 = 1; 

Передаточная функция замкнутой системы по первому каналу возмущения имеет следующий вид:

;

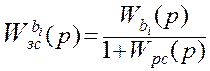Представим в показательной форме:

;

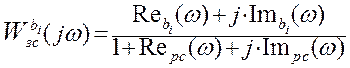Для построения переходного процесса в замкнутой системе по первому каналу возмущения необходимо найти ВЧХ этой замкнутой системы.

;

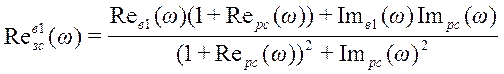 где     ;

;

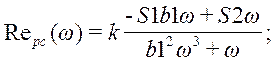
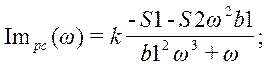
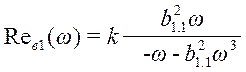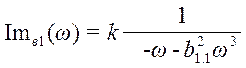На рис. 68  изображен график ВЧХ по первому каналу возмущения.

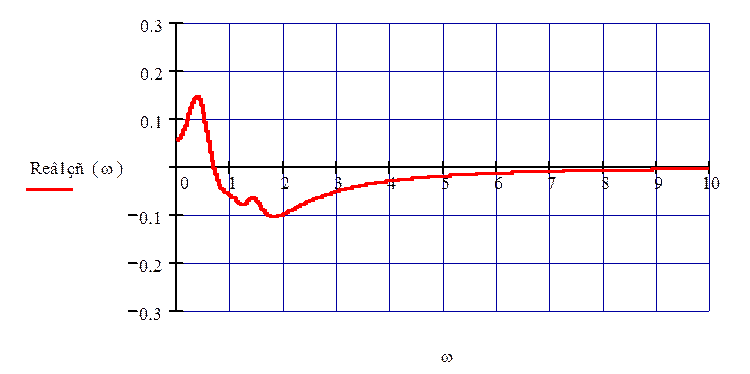
Рисунок 68 – ВЧХ по первому каналу возмущения

По выражению для ВЧХ строим график переходного процесса замкнутой системы для первого канала возмущения (рис. 69).

;

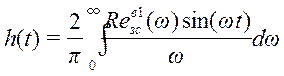Данные для построения переходного процесса по первому каналу возмущения представлены в таблице 12.1

Таблица 12.1 

t	0	2	4	6	8	10	12	14	16
h(t)	0	0.067	0.121	0.111	0.072	0.055	0.048	0.055	0.056

       

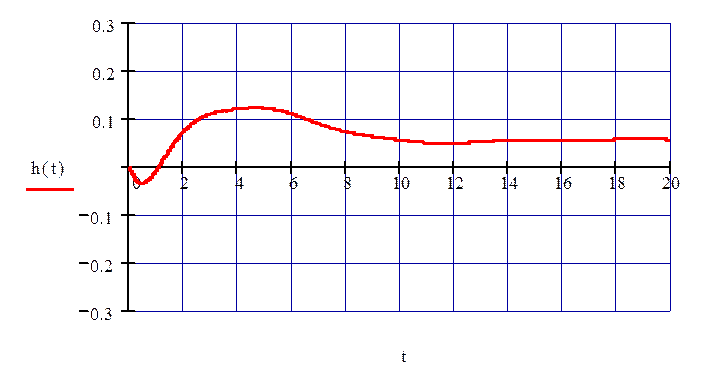
Рисунок 69 –  Переходный процесс замкнутой системы по 1 каналу возмущения

12.2  Второй канал возмущения

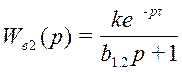 где k = 0,5; b_1.2 = 6; τ = 3

Передаточная функция замкнутой системы по второму каналу возмущения имеет следующий вид:

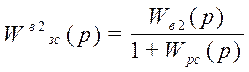
Представим в показательной форме:

;

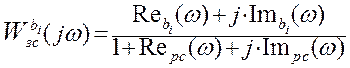Для построения переходного процесса в замкнутой системе по первому каналу возмущения необходимо найти ВЧХ этой замкнутой системы.

;

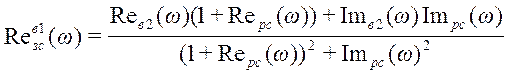 где   ;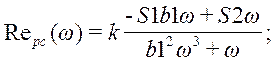

;

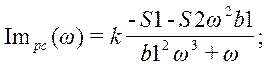
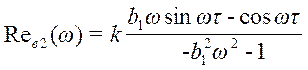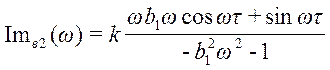На рис. 70  изображен график ВЧХ по второму каналу возмущения.

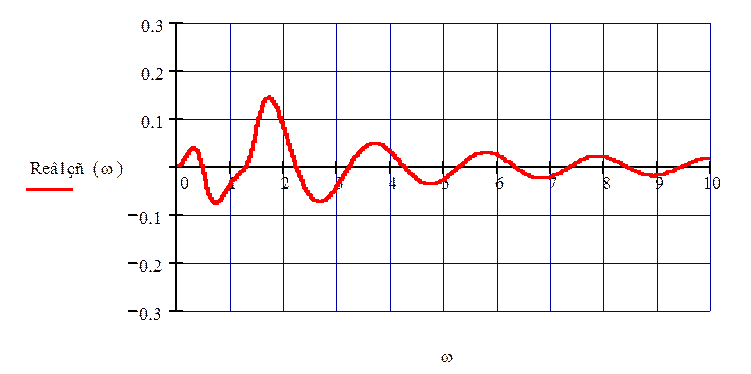
                 Рисунок 70 – ВЧХ по второму каналу возмущения

По выражению для ВЧХ строим график переходного процесса замкнутой системы для первого канала возмущения (рис. 71).

;

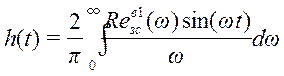Данные для построения переходного процесса по второму каналу возмущения представлены в таблице 12.2.

Таблица 12.2 

t	0	2	4	6	8	10	12	14	16
h(t)	0	-0.01	0.036	0.028	0.027	0.003	-0.001	-0.002	-0.0002

    

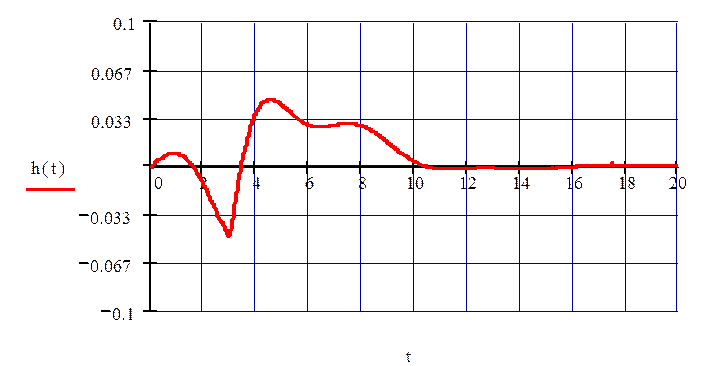
Рисунок 71 –  Переходный процесс замкнутой системы по 2 каналу возмущения

12.3  Третий канал возмущения

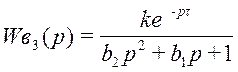 , где k = 0,5; b_3.2 = 400; b_3.1 = 32; τ = 10;

Передаточная функция замкнутой системы по третьему каналу возмущения имеет следующий вид:

;

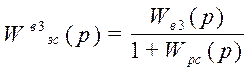Представим в показательной форме:

;

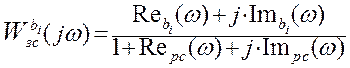Для построения переходного процесса в замкнутой системе по первому каналу возмущения необходимо найти ВЧХ этой замкнутой системы.

;

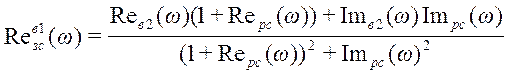 где    ;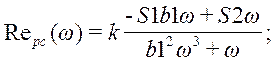 

;

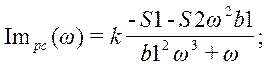
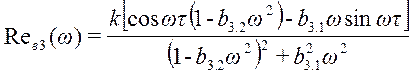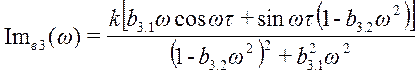На рис. 72  изображен график ВЧХ по третьему каналу возмущения.

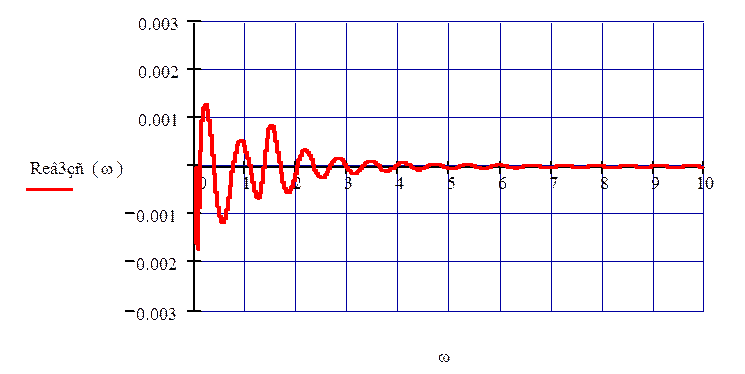
Рисунок 72 – ВЧХ по второму каналу возмущения

По выражению для ВЧХ строим график переходного процесса замкнутой системы для первого канала возмущения (рис. 73).

;

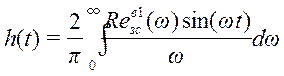Данные для построения переходного процесса по третьему каналу возмущения представлены в таблице 12.3.

Таблица 12.3. 

t	0	10	20	30	40	50	60	70	80
h(t)	0	3×10-4	-1×10-3	-1.3×10-3	-1.1×10-3	-8×10-4	-6×10-4	-4×10-4	-2×10-4

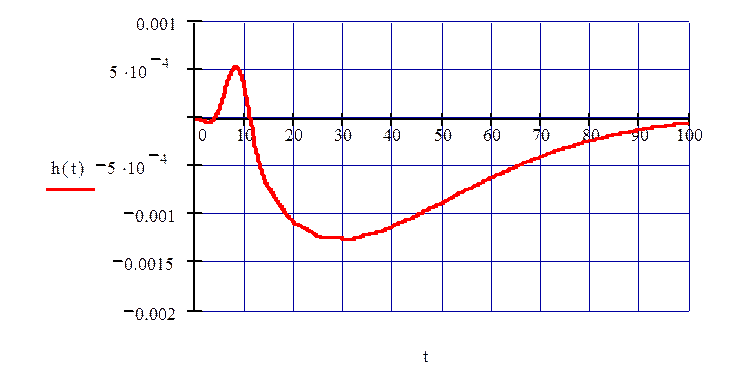
Рисунок 73 – Переходный процесс замкнутой системы по 3 каналу возмущения

13. Определение нулей и полюсов передаточных функций замкнутой системы по каналам управления и возмущения

Для получения корневых показателей качества системы управления необходимо рассчитать корни полиномов числителя и знаменателя передаточной функции замкнутой системы для случаев, когда запаздывание в канале регулирования равно нулю. Для этого необходимо в общие функции замкнутой системы подставить конкретные выражения передаточных функций объекта и регулятора и привести W_зс(p) к отношению произведений полиномов.