Математические методы в планировании производства: Лабораторный практикум, страница 8

Пример 1.6

Рассмотрим М-стадийную последовательную систему с несколькими производственными процессами и межстадийным (межоперационным) запасом на каждой стадии.. Система производит один вид конечного продукта. На единицу конечного продукта требуется одна единица полуфабриката, производимого каждой стадией. На каждой стадии имеется несколько производственных мощностей (процессов, источников продукции), таких как основное время, сверхурочное время, закупка у субподрядчика и т. п. Пусть

 - число единиц продукции, производимое на стадии j процессом k, k = 1, 2, … K_j, j = 1, 2, …M;

 - производственные затраты на единицу продукции на стадии j при использовании процесса k;

 - количество ресурса типа , максимально доступное на стадии ,  = 1, 2, …; 

 - количество ресурса типа , расходуемое на производство единицы продукта на стадии  процессом ;

 - число единиц конечной  продукции, которое необходимо произвести в планируемом периоде;

- суммарные производственные затраты (целевая функция).

Необходимо найти такие значения всех переменных , которые минимизируют  функцию

при следующих ограничениях:

1.  Предельные количества доступных ресурсов на каждой стадии:

,  = 1, 2, …M,  = 1, 2, …;

2.  Баланс запасов между стадиями:

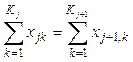,  = 1, 2, …M – 1;

3.  Спрос на конечную продукцию:

.

Приведенная в данном примере модель легко обобщается на случай, когда на каждой стадии производится несколько промежуточных продуктов, а конечные  продукты производятся только на последней стадии. Могут быть варианты структуры модели, когда каждый продукт предыдущей стадии используется только для одного продукта на последующей, или когда продукт, полученный на одной стадии, может использоваться в производстве нескольких продуктов на последующих стадиях. Далее рассмотрим пример именно такой структуры.

Пример 1.7

Структура трехстадийной системы изображена на рисунке 1.

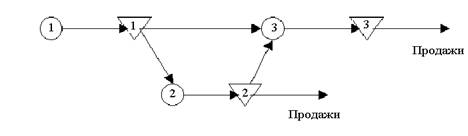
Рисунок 1 –Производственная система для примера 1.7

Продукт, производимый стадией 1, используется в производстве продуктов на стадиях 2 и 3. Продукт стадии 2 используется в производстве продукта стадии 3 а также может продаваться потребителям. Продукт стадии 3 является конечным продуктом, нигде далее в производстве не используется и продается потребителям. Обозначим через

 - планируемый объем выпуска на стадии ;

 - максимальная производительность на стадии ;

 - число единиц продукта стадии , необходимое для производства одной единицы продукта стадии ;

 - затраты на производство единицы продукта на стадии ;

 - доход от реализации единицы продукции стадии , ;

 - минимальное значение потребности для продукта ;

 - максимальное значение потребности для продукта ;

 - целевая функция, суммарная прибыль от реализации продукции.

Таким образом, требуется найти максимум функции:

.

при ограничениях:

, j = 1, 2, 3;

;

;

;

.

Другой вид этой же модели можно получить, если ввести дополнительные переменные  и , представляющие объемы продаж продуктов 2 и 3. В этой модели максимизируется целевая функция:

.

при ограничениях:

, j = 1, 2, 3;

;

;

;

;

.

Упражнения

1 Решите задачу из примера 1.1. Определите «узкие места» и исследуйте влияние ослабления ограничений.

2 Завод производит три вида продукции. Необходимо составить план выпуска продукции на предстоящий отрезок времени, то есть определить, какое количество продукции каждого вида следует произвести, чтобы получить максимальную прибыль. Необходимые данные приведены в таблице.

Продукт	Время обработки, час/ед					При быль за ед.	Продажи
	Цех 1	Цех 2	Цех 3	Контроль	Отгру зка		Min	Max
А	0,14	0,60	0,20	0,04	0,10	42	180	250
В	0,10	0,40	0,20	0,04	0,10	40	200	400
С		0,20	0,10	0,04	0,12	36	360	500
Доступное время работы за период	160	320	160	80	82