Математические методы в планировании производства: Лабораторный практикум, страница 19

Если сетевой график содержит только одну завершающую работу, то есть работу, у которой нет последующих, то длина критического пути равна наиболее раннему моменту завершения этой работы.

3.1.3  Алгоритм определения  - поздних моментов завершения работ и критического пути

Введем обозначения:

 - момент наиболее позднего завершения работы ;

 - момент наиболее позднего начала работы , .

Множество всех работ, непосредственно следующих за работой , обозначим как . Предыдущий алгоритм вычислял моменты наиболее раннего начала всех работ, начиная с первых работ в графике. Алгоритм определения наиболее поздних моментов завершения работ начинает вычисления с последней работы в графике. Для нее момент наиболее позднего завершения уже известен после работы предыдущего алгоритма, это  - наиболее ранний момент завершения всех работ графика. Двигаясь вспять по сетевому графику, алгоритм последовательно определяет моменты наиболее позднего завершения каждой работы  таким образом, чтобы моменты наиболее позднего завершения последователей работы  не изменялись, поскольку они уже вычислены. Момент наиболее позднего завершения работы  равен минимальному из моментов наиболее позднего начала всех последователей .

В примере, изображенном на рисунке 5 работа  имеет три последователя – работы 1, 2 и 3. Моменты наиболее позднего их завершения – это ,  и , и они уже вычислены. Следовательно, известны и моменты наиболее позднего начала каждой из этих работ    и . Работа  должна быть закончена до начала любой из работ 1, 2, 3, но как можно позднее. В качестве момента наиболее позднего завершения работы  выбирается  -момент наиболее позднего начала работы 3, так как его значение минимально из всех трех работ. Если в качестве  выбрать  или , то работа  завершится после начала работы 3, что недопустимо.

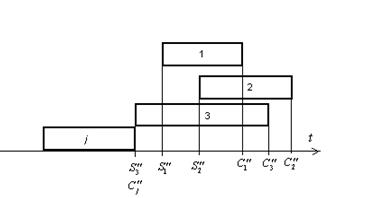
Рисунок 5 – Определение момента наиболее позднего завершения работы

Алгоритм определения наиболее поздних моментов завершения работ:

1. := и := для всех работ , у которых нет последующих работ (конечных).

2. Вычислить последовательно для каждой работы : , где минимум ищется по всем значениям , принадлежащим  множеству , и .

3 Проверить, что для каждой работы , не имеющей предшественников (начальной) , =0.

4. Конец алгоритма.

После выполнения этих двух алгоритмов будут известны моменты наиболее раннего -  и  - наиболее позднего окончания всех работ. Те работы, у которых оба эти момента равны, не имеют резерва времени. Они называются критическими работами и их совокупность образует один или несколько критических путей.

3.1.4 Резервы времени работ

Работы, не лежащие на критическом пути, имеют резервы времени.

Максимальное время, которое может быть отведено на выполнение работы , очевидно, равно . Вычтем из этой величины длительность работы и получим резерв времени:

.

Этот резерв времени работы называется полным резервом, он принадлежит всем полным путям графа, проходящим через эту работу.

Частный резерв времени первого вида - это часть полного резерва, на которую можно увеличить продолжительность работы, не изменив позднего момента начала работы:

.

Этот резерв - то, что остается от интервала между поздним началом и поздним завершением, когда из него вычтена длительность работы.

Частный резерв времени второго вида, или свободный резерв, - это часть полного резерва, на которую можно увеличить продолжительность работы, не изменив раннего срока ее завершения. Здесь в качестве интервала, внутри которого должна быть выполнена работа берется разность между ранним завершением и ранним началом:

.

Независимый резерв r_нj - то, что остается от интервала между поздним началом и ранним завершением, когда из него вычтена длительность работы. Использование этого резерва не влияет на оставшиеся резервы у других работ:

Пример 3.2

Имеется 14 работ, времена выполнения которых приведены в таблице 9, а ограничения предшествования заданы графом на рисунке 6.

Таблица 9 – Время выполнения работ для примера 3.2