Экономика и менеджмент \ Математические методы в планировании производства

Математические методы в планировании производства: Лабораторный практикум, страница 20

j

1

2

3

4

5

6

7

8

9

10

11

12

13

14

5

6

9

12

7

12

10

6

10

9

7

8

7

5

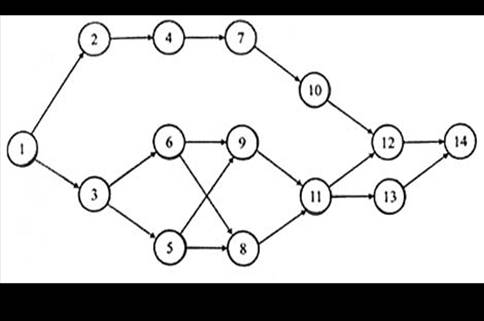
Безимени-1

Рисунок 6 – Сетевой график для примера 3.2

В результате выполнения алгоритма прямого хода (от вершины 1 до вершины 14) получим значения наиболее ранних моментов завершения всех работ , в том числе и =56 - время завершения всех работ графика. Выполнив алгоритм обратного хода (от вершины 14 до вершины 1) получим моменты наиболее позднего завершения всех работ . Работы, у которых =, находятся на критическом пути. Значения всех вычисленных моментов приведены в таблице 3.4. Критический путь образуют работы 1, 3, 6, 9, 11, 12, 14, и он является единственным. Остальные работы имеют резервы времени.

Таблица 10 – Результаты расчета для примера 3.2

j

1

2

3

4

5

6

7

8

9

10

11

12

13

14

5

6

9

12

7

12

10

6

10

9

7

8

7

5

-

1

1

2

3

3

4

5

6

5

6

7

8

9

10

11

11

12

13

0

5

5

11

14

14

23

26

26

33

36

43

43

51

5

11

14

23

21

26

33

32

36

42

43

51

50

56

2

3

4

5

6

7

8

9

8

9

10

11

11

12

12

3

14

14

-

5

12

14

24

26

26

34

36

36

43

43

51

51

56

0

6

5

12

19

14

24

30

26

34

36

43

44

51

Упражнения

1 Заданы технологические маршруты для трех деталей (работ):

Работы

Операции: машина

1

2

3

4

J1

M2

M3

-

-

J2

M3

M1

M2

М1

J3

M2

M3

M1

-

Порядок запуска деталей в обработку (приоритет) совпадает с нумерацией работ.

Заданы длительности операций для каждой работы:

Работа J1:

Номер варианта

Номер операции

1

2

3

4

1

7

4

-

-

2

11

2

-

-

3

5

7

-

-

4

8

3

-

-

5

5

9

-

-

6

10

6

-

-

7

1

8

-

-

8

4

3

-

-
Скачать файл