Математические методы в планировании производства: Лабораторный практикум, страница 6

2.  Ограничение баланса материалов (суммарный вес всех составляющих после удаления примесей равен одной тонне:

.

Коэффициенты в этом равенстве представляют содержание основных компонент (за исключением примесей) в каждом виде руды.

Значения переменных в оптимальном решении равны:

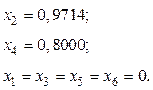
Это значит, что для получения одной тонны сплава мы должны использовать 0,9714 тонны руды 2 и 0, 8 тонны руды 4. Затраты на руду составят 27,43 доллара на тонну сплава.

Ограничение на максимальное содержание металла С в сплаве (не более 4%) является существенным – оно выполняется как равенство в оптимальном решении. Значение для этого ограничения равно 28,57 доллара на 100%. Таким образом, ослабление этого ограничения на 1% (задание его на уровне не 4%, а 5%) даст снижение затрат на руду на 0,2857 доллара на тонну сплава.

1.4 Одновременное производство нескольких продуктов одним процессом

Имеется исходный материал, который может быть обработан несколькими способами. При обработке материала из него получается несколько различных продуктов. Способы обработки различаются тем, что при каждом способе получаются различные количества готовых продуктов, а также  затратами на обработку единицы исходного материала. Требуется определить, какое количество исходного материала необходимо обработать каждым из способов, чтобы получить заданные количества готовых продуктов с минимальными затратами.

Пусть  - количество исходного материала, обработанного методом j, j = 1, 2, …n, а  - требуемое количество продукта i, i = 1, 2, … m. Одна единица материала, обработанная методом j, дает  единиц продукта i. Затраты на обработку методом j составляют  на единицу исходного материала. Требуется минимизировать суммарные издержки

при ограничениях:

.

При необходимости могут быть добавлены ограничения на количества исходного материала, которые могут быть обработаны различными методами. Нетрудно обобщить эту модель на случай, когда имеется несколько видов исходных материалов.

Пример 1.4

Бумагоделательная машина производит рулоны бумаги шириной 200 см. Потребителям отгружается бумага меньшей ширины, то есть рулоны разрезаются по ширине на отдельные части заданного размера. На данный период заказчикам требуется 500 рулонов шириной 45 см, 300 шириной 24 см и 200 шириной 60 см.

Требуется составить план разрезки 200-сантиметровых рулонов на рулоны требуемой ширины в количествах не менее, чем заказанные на каждый размер.

Список возможных способов разрезки стандартных рулонов приведен в таблице 6. Например, при разрезке одного рулона по способу 2 получаются 3 рулона шириной 24 см, 2 рулона шириной 60 см и неиспользуемый остаток (отходы) шириной 8 см.

Таблица 6 – Способы разрезки

Обозначим через  число стандартных (исходных) рулонов, которые будут разрезаны по варианту j. Если все оказавшиеся лишними 45-,24- или 60-сантиметровые рулоны вместе с остатком уходят в отходы, то целевую функцию можно записать в виде:

, то есть, мы хотим минимизировать общее количество разрезаемых 200-сантиметровых рулонов, которое потребуется для выполнения заказа. Полученное количество рулонов каждой ширины должно быть не менее, чем затребовано заказчиками: