Математические методы в планировании производства: Лабораторный практикум, страница 3

Тогда задача оптимального планирования состоит в нахождении неотрицательных значений этих переменных, дающих максимум функции    

L = 4x₁ + 10x₂ + 5x₃ + 6x_4.

Таблица 1 - Темп производства в часах на единицу продукции

	Номер продукта				Фонд
Рабочий центр	1	2	3	4	времени
Штамповка	0,03	0,15	0,05	0,10	400
Сверление	0,06	0,12	0	0,10	400
Сборка	0,05	0,10	0,05	0,12	500
Отделка	0,04	0,20	0,03	0,12	450
Упаковка	0,02	0,06	0,02	0,05	400

Таблица 2 - Затраты, цены и пределы объемов  продаж

Продукт	Цена продажи	Затраты на ед.	Пределы объемов продаж
			Минимум	Максимум
1	10	6	100	6000
2	25	15	0	500
3	16	11	500	3000
4	20	14	100	1000

при ограничениях на время производства:

0,03x₁ + 0,15x₂ + 0,05x₃ + 0,10x₄ <= 400 (штамповка),

0,06x₁ + 0,12x₂               + 0,10x₄ <= 400 (сверление),

0,05x₁ + 0,10x₂ + 0,05x₃ + 0,12x₄ <= 500 (сборка),

0,04x₁ + 0,20x₂ + 0,03x₃ + 0,12x₄ <= 450 (отделка),

0,02x₁ + 0,06x₂ + 0,02x₃ + 0,05x₄ <= 400 (упаковка);

на ресурсы:

2,0х₂ + 1,2х₄ <= 2000;

и на объемы продаж:

100 <= x₁ <= 6000,

0 <= x₂ <= 500,

500 <= x₃ <= 3000,

100 <= x₄ <= 1000.

Решив сформулированную задачу линейного программирования, получим оптимальный план:

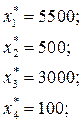
Второй и третий продукты должны производиться в объемах, равных максимальным продажам, а четвертый продукт – в объеме минимальных продаж.

Полученная программа полностью использует производственную мощность на штамповке и сверлении.

Неиспользованная производственная мощность на других рабочих центрах составляет 13 часов на сборке, 28 часов на отделке и 195 часов на упаковке.

Из 2000 м² листа использовано 1120 и 880 осталось неиспользованным.

Максимальное значение прибыли равно 42600.

Рассмотрение двойственных переменных задачи показывает влияние ограничений на максимальное значение прибыли. Так, увеличение производственной мощности штамповки (в оптимальном решении она использована полностью) на один час увеличивает максимальную прибыль на 22,22, для сверления – на 55,56. На одну единицу продукта 3, проданную сверх ограничения в 3000 единиц можно получить 3,89 дополнительной прибыли. Заметьте, что не 5, как следует из таблицы 2.2, а меньше, так как при увеличении выпуска продукта 3 уменьшится выпуск других продуктов.

1.2 Модель выбора процессов (способов) производства

В этой задаче потребность в каждом из n видов продукции будем считать известной. Для каждого продукта имеется несколько возможных способов производства (технологические маршруты, процессы, производственные подразделения, источники – собственное производство или субподрядчики, основное время или сверхурочное). Издержки и затраты ресурсов на единицу продукции при каждом способе производства различны. Планирование ведется на один отрезок времени, рассматриваемый независимо от других. Производственные ресурсы (и производительность каждого источника продукции тоже) ограничены. Они должны быть распределены между продуктами так, чтобы суммарные издержки производства были минимальны.

В этой задаче требуется определить, какое количество каждого продукт должно быть произведено каждым способом.

В качестве критерия оптимизации можно использовать суммарные издержки.

Введем обозначения:

 - количество продукта i, i ,= 1, 2,…n, производимое процессом j, j = 1, 2,…J_i;