Математические методы в планировании производства: Лабораторный практикум, страница 18

Таблица 7 – Технологические маршруты для четырех работ и трех машин

Работы	Операции: машина и длительность
J1	M2 (3)	M3 (7)
J2	M3 (5)	M1 (6)	M2 (4)
J3	M2 (8)	M3 (6)	M1 (4)
J4	M1 (4)	M3 (3)	M2 (4)

а)

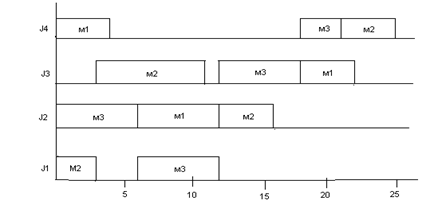
б)

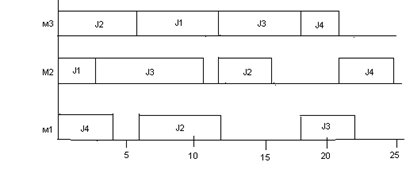
Рисунок 2 – Диаграммы Гантта: а) - для работ, б) – для машин

3.1 Управление проектами

3.1.1  Критический путь и и его длина

Критический путь – последовательность работ, определяющая длительность всего проекта, то есть время выполнения всех работ проекта, и значение этой длительности, .

Метод основан на представлении комплекса работ в виде графа.

Пример 3.1

Имеется 8 работ, отношения предшествования для которых даются таблицей 8.

Таблица 8 – Данные для примера 4.1

Работы	Непосредственные предшественники	Непосредственные последователи
1	-	4
2	-	5
3	-	6,7
4	1	6,7
5	2	6
6	3,4,5	8
7	3,4	8
8	6,7	-

Сетевой график для этой задачи приведен на рисунке 3. На нем добавлена фиктивная работа с номером 0, имеющая нулевую длительность. Это необходимо для того, чтобы граф имел только одну исходную вершину.

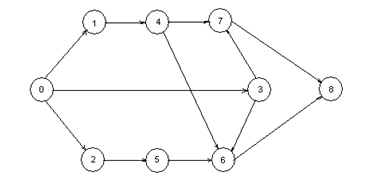
Рисунок 3 – Сетевой график

Считается, что каждая работа может начинаться немедленно после того, как выполнены все ее непосредственные предшественники. Ресурсы, необходимые для выполнения работы, считаются, всегда доступными, то есть фактически неограниченными.

Главная задача метода критического пути (CPM) - определить время, которое потребуется для выполнения всего комплекса работ. Начальную работу 0 и конечную 8 связывают несколько цепочек (путей) на графе.

Цепочка, имеющая наибольшую длительность, и будет определять время выполнения всего проекта. Эта цепочка и называется критическим путем.

Таким образом, алгоритм обработки сетевых графиков должен находить критический путь и определять его длительность.

3.1.2  Алгоритм определения  - моментов раннего завершения работ и вычисления

Рассмотрим  работ, подверженным ограничениям предшествования. Длительность каждой работы  фиксирована и равна .

Обозначение  - множество всех работ, которые непосредственно предшествуют работе . Работа  может начаться только после того, как выполнены все работы из этого множества.

Обозначим через  момент наиболее раннего завершения работы ,  - наиболее ранний момент начала работы  (это момент времени, к которому завершаются все работы, непосредственно предшествующие работе ). Очевидно, что этот момент совпадает с моментом завершения последней (по времени) работы из множества .

.

Рисунок 4 иллюстрирует выбор наиболее раннего момента начала работы . Непосредственными предшественниками работы  на этом рисунке являются работы 1, 2, 3 и 4. Все они заканчиваются в разное время. В качестве момента наиболее раннего начала работы  мы должны выбрать момент завершения работы 2, так как он имеет максимальное значение из всех четырех.

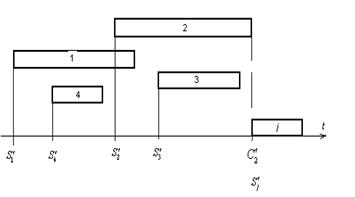
Рисунок 4 – Определение наиболее раннего момента начала работы

Алгоритм определения наиболее ранних моментов начала всех работ и вычисления длины критического пути теперь очевиден:

1.  и  для всех работ, не имеющих предшественников.

2. Вычислить последовательно для каждой работы   где максимум ищется по всем значениям , принадлежащих множеству , и .

3. Длина критического пути равна .

4. Конец алгоритма.

В этом алгоритме на шаге 2 для каждой работы  находится та предшествующая работа, которая и определяет наиболее ранний момент начала работы . Все другие предшествующие работы отсекаются на этом шаге. Потому для нахождения критического пути нет необходимости вычислять длительности всех цепочек и сравнивать их.