Факторный анализ результатов испытаний тепловозов. В результате статистической обработки опытных данных исключены промахи, осреднены показатели, установлен вид закона распределения, оценена точность измерений и колеблемость показателей. Полученные сведения используют для факторного анализа – исследования корреляционных связей и установления регрессионных зависимостей результативных показателей от факторных с целью прогнозирования и изыскания предпочтительных решений. При этом целесообразно для построения математической модели тяги использовать метод идентификации – находить зависимости лишь между входными и выходными параметрами.
Весьма важно отсеить второстепенные и выявить наиболее существенные факторы, определяющие режим и эффективность тяги. Для этих целей используют метод корреляционного анализа.
Результативным называют показатель, зависимый от другого – факторного показателя. Корреляционной связью называют такую, при которой на значение результативного показателя оказывают влияние не только факторный, но и множество других.
Две величины связаны корреляционно, если изменение среднего значения одного признака изменяет среднее значение другого. Задача корреляционного анализа опытного материала сводится к определению: наличия, формы и тесноты взаимосвязи (соотношения) между показателями, когда результативный показатель определяется факторным не полностью и нет возможности изолировать влияние других факторов. Такое свойство соотношений величин является прямым отражением реального процесса тяги в условиях эксплуатации. Разумеется, выбор корреляционных связей надо производить исходя из физической природы явлений. Лучшей для этих целей должна служить исходная информация теории тяги поездов. Тесноту корреляционных связей двух случайных величин вполне приемлемо оценивать линейным коэффициентом корреляции ryx, который изменяется в пределах от– 1 до + 1, прямые связи со знаком (+), обратные со знаком (–). Чем больше ryx, тем теснее связи, однако они не должны быть коллинеарными, когда корреляционная связь уступает место функциональным зависимостям (при ryx = 0,85 - 0,9).
Для расчета коэффициента парной корреляции удобна формула
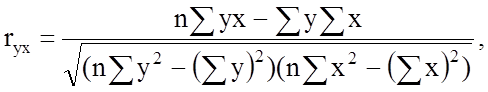
где у- результативный показатель; х – факторный показатель; n – число опытов.
Порядок и правила построения эксплуатационной модели тяги поездов. Использование модели на практике.
На основе корреляционного анализа опытного материала необходимо дать математическое описание поведения результативного показателя под влиянием совокупности факторов и того или иного переменного факторного в частности, что является задачей регрессионного анализа. Проигрывание факторной модели на ЭВМ должно раскрыть значимость различных факторов и выбор наиболее эффективных способов интенсификации тяги в конкретных условиях эксплуатации.
Обобщенно порядок и правила построения многофакторной эксплуатационной модели тяги сводится к следующему.
1. В качестве исходных позиций следует признать, что режимы и процессы тяги, поведение показателей состояния поезда и показателей эффективности обусловлены: технологией и функцией цели перевозочного процесса, неуправляемым воздействием внешней среды, физической природой тягово-энергетических процессов в системе локомотив – состав, закономерностью распределения совокупности взаимосвязанных случайных факторов.
2. Установить, по какому результативному признаку будет произведен факторный анализ, исходя из целевой функции объекта тяги и технологии перевозочного процесса.
3. Отобрать для включения в модель наиболее существенные факторы. Перечень факторов не должен быть широким, так как чем больше факторов включается в модель, тем больше опытов необходимо производить.
4. Выбор результативного и факторного показателей должен быть теоретически обоснован закономерностями механики, физики, теории тяги поездов, информацией паспортных характеристик.
5. Массовые вероятностные процессы характеризуются прежде всего средним значением параметров, которые являются случайными и образуются в результате массового явления под влиянием многих факторов. Чтобы закон нормального распределения случайных величин мог проявиться, факторные показатели должны быть независимыми и нерезко выделяющимися. В то же время минимальное число опытов должно быть как можно больше, чтобы обеспечить достаточную достоверность исследований. Как показал опыт, для эксплуатационных испытаний тепловозов их должно быть не менее 20–25. Однако во всех случаях гипотеза о нормальном законе распределения должна быть проверена. Проще это сделать по критерию W, применяемому при малом числе опытов.
6. Связи между факторами не должны быть функциональными. Коэффициент парной корреляции в пределах 0,8–0,95 указывает на наличие коллинеарности.
7. Для того чтобы установить, с какой степенью точности можно делать выводы о генеральной совокупности случайных величин, необходимо установить доверительную вероятность и рассчитать доверительный интервал по критерию Стьюдента.
8. Произвести дисперсионный анализ, определить оценки показателей, средние квадратичные отклонения.
9. Рассчитать парные коэффициенты корреляции главных факторов, установить тесноту и форму связи, определить их значимость.
10. Построить многофакторную модель тяги поездов в форме уравнения множественной регрессии, проверить надежность коэффициентов регрессии.
Уравнение множественной регрессии имеет вид
где 
- среднее значение функции х1,
соответствующее заданным значениям переменных (аргументов) х2, х3,
… хр; b1, b2,
…, bp – коэффициенты корреляции, которые
последовательно определяют из систем уравнений, составленных на основании
принципа наименьших квадратов, начиная с парной корреляции.
11. Произвести проверку на адекватность математической модели оригиналу по критерию Фишера F.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.