, где Евн
и Р — напряженность поля и поляризованность диэлектрика, теорема Гаусса
принимает вид
, т.
е. поток вектора D через произвольную замкнутую поверхность равен только
суммарному свободному заряду, находящемуся внутри этой поверхности. Вектор D
называется вектором электрической индукции (иногда используют эквивалентный
термин «вектор электрического смещения»). Именно независимость потока вектора
электрической индукции от поляризационного заряда во многом обуславливает
удобство использования вектора D.
Теорема Гаусса для вектора электрической индукции справедлива всегда, т. е. для электрических полей любой природы, а не только электростатических.
2.6. Граничные условия на границе раздела диэлектриков
Выясним, как связаны между собой компоненты векторов D и Е по разные стороны от границы раздела диэлектриков I и II. Для этого рассмотрим сначала цилиндрическую поверхность пренебрежимо малой высоты, оба «донышка» которой параллельны границе раздела и лежат по разные стороны от нее (см. рис. 15а).
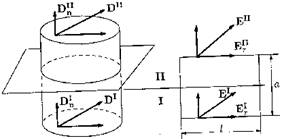
а) б)
Рис. 15
По теореме Гаусса поток вектора D через всю цилиндрическую поверхность S равен нулю, так как внутри нее есть только поляризационные заряды. Поток через боковую поверхность пренебрежимо мал, так как пренебрежимо мала ее площадь, поэтому поток вектора через нижнее «донышко» равен потоку через верхнее «донышко»:
.
Отсюда следует, что нормальные компоненты векторов электрической индукции в граничащих диэлектриках равны друг другу:
.
Рассмотрим теперь изображенный на рисунке маленький прямоугольный замкнутый контур, стороны (которого параллельны границе раздела, а ширина а много меньше длины l (см. рис. 15б). Ранее было указано (см. параграф 1.3), что интеграл по замкнутому контуру от напряженности равен нулю
Для изображенного на рисунке контура этот интеграл равен разности
так как ширина а пренебрежимо мала. Поэтому равны друг другу тангенциальные компоненты векторов напряженности электрического поля в граничащих диэлектриках:
2.7. Плоский конденсатор. Емкость
Плоский конденсатор — это две пластины, называемые обкладками, расположенные на малом расстоянии друг от друга. Зазор между обкладками часто заполняют диэлектриком.
Пусть имеется конденсатор, площадь обкладки которого равна S, расстояние между обкладками d, свободный заряд на одной обкладке +Q, а на другой -Q (см. рис. 16). Из теоремы Гаусса следует (вычисления совершенно аналогичны расчету поля заряженной плоскости), что каждая из обкладок создает поле с электрической индукцией
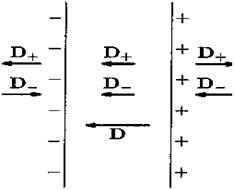
Рис.16
Между обкладками векторы электрической индукции, создаваемые каждой из обкладок, направлены в одну сторону, вне конденсатора - индукции направлены в разные стороны. Поэтому результирующая индукция отлична от нуля только внутри конденсатора.
Очевидно, эта результирующая индукция равна
откуда получаем, что напряженность поля внутри конденсатора есть
Так как потенциал связан с напряженностью соотношением
разность потенциалов между обкладками равна интегралу от напряженности по координате, т. е. в данном случае
Разность потенциалов между обкладками конденсатора называют напряжением конденсатора и обозначают буквой U.
Мы получили, что напряжение плоского конденсатора равно
Разность потенциалов между обкладками конденсатора называют напряжением конденсатора и обозначают буквой U.
Видно, что напряжение U пропорционально заряду Q и некоторому коэффициенту, зависящему от геометрии конденсатора и диэлектрической проницаемости диэлектрика. Отношение заряда конденсатора к его напряжению
называется емкостью конденсатора. Емкость плоского конденсатора равна
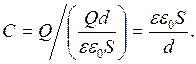
Единица измерения емкости — Фарада.
2.8. Соединение конденсаторов
Параллельное соединение. Два конденсатора, параллельно соединенные проводниками, могут быть представлены как один эквивалентный конденсатор (см. рис. 17). Определим его емкость. Очевидно, что потенциалы обоих конденсаторов равны, суммарный заряд равен сумме зарядов каждого конденсатора
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.