Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 5

Мы получили, что поток вектора напряженности электрического поля от одного точечного заряда, проходящий через любую замкнутую поверхность, пропорционален величине этого заряда, если заряд находится внутри поверхности, и равен нулю, если заряд вне поверхности. Но любая система зарядов может быть представлена как совокупность точечных зарядов; поле, создаваемое системой зарядов, есть сумма полей каждого заряда. Итак, получаем окончательную формулировку теоремы Гаусса: поток вектора напряженности электрического поля через произвольную замкнутую поверхность равен сумме зарядов, находящихся внутри этой поверхности, разделенной на :

Еще раз подчеркнем, что теорема Гаусса, хотя и получена нами из закона Кулона, имеет самый общий характер и справедлива всегда, а не только для электростатических полей.

1.6. Поле заряженной сферы, нити и плоскости

Равномерно заряженная сфера. Проведем вокруг заряженной сферы сферическую поверхность радиуса г с центром, совпадающем с центром сферы (см. рис. 9). Из соображений симметрии очевидно, что вектор напряженности поля Е в произвольной точке сферы лежит на прямой, соединяющий эту точку и центр, т. е. совпадает с направлением нормали. Из симметрии также очевидно, что величина напряженности одна и та же во всех точках сферической поверхности. Поэтому поток вектора через сферическую поверхность равен произведению Е на площадь сферической поверхности:

.

В силу теоремы Гаусса этот поток пропорционален суммарному

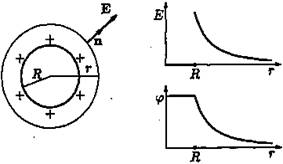
Рис. 9

 

заряду, находящемуся внутри сферической поверхности.

Если сферическая поверхность имеет радиус больший, чем радиус заряженной сферы, то находящийся внутри заряд есть, очевидно, заряд заряженной сферы Q. Поэтому

откуда напряженность поля равна

 если r > R.

Если же сферическая поверхность лежит внутри заряженной сферы, то заряд внутри этой сферической поверхности равен нулю, следовательно напряженность равна нулю:

E= 0, если r > R.

Итак, напряженность поля заряженной сферы совпадает с напряженностью поля точечного заряда вне заряженной сферы, и равна нулю внутри заряженной сферы.

Зная напряженность поля, создаваемого в каждой точке пространства заряженной сферой, легко определить в каждой точке и потенциал по формуле (потенциал на бесконечности принимаем равным нулю)

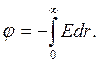
Везде внутри заряженной сферы потенциал имеет одно и то же значение, а вне заряженной сферы потенциал обратно пропорционален расстоянию до ее центра:

 

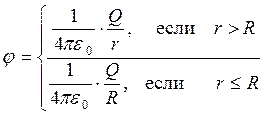
Равномерно заряженная нить. Проведем вокруг заряженной нити цилиндрическую поверхность, ось которой совпадает

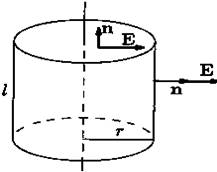
Рис. 10

с нитью (см. рис. 10). Во всех точках этой поверхности вектор Е направлен перпендикулярно заряженной нити (это очевидно из соображений симметрии). Следовательно, поток вектора Е через оба «донышка» цилиндрической поверхности равен нулю, так как здесь векторы Е и n перпендикулярны друг другу. На всей же боковой поверхности векторы Е и n направлены параллельно, поэтому полный поток равен потоку только через боковую поверхность:

N = E·S = E · 2πrl,

где S — площадь боковой поверхности, l- высота цилиндра, r -радиус цилиндра. По теореме Гаусса поток этот равен

    

или

где  — линейная плотность заряда нити (т. е. величина заряда, приходящаяся на единицу длины нити). Приравнивая, получаем

;                       

Таким образом, напряженность электрического поля заряженной нити прямо пропорциональна линейной плотности заряда  и обратно пропорциональна расстоянию до нити r.

Равномерно заряженная плоскость. Проведем цилиндрическую поверхность, ось которой перпендикулярна заряженной плоскости (см. рис. 11).Из симметрии следует, что            

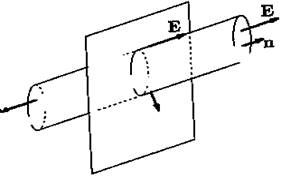
Рис. 11

вектор Е направлен перпендикулярно заряженной плоскости. Поэтому поток вектора напряженности через боковую поверхность цилиндра равен нулю; весь поток через цилиндрическую поверхность складывается только из потоков через «донышки» цилиндра.