1.4. Силовые линии и эквипотенциальные поверхности
Для наглядного изображения электрических полей часто рисуют силовые линии. Силовая линия — это линия, касательная к которой в каждой точке совпадает с направлением вектора напряженности в этой точке. Очевидно, что силовые линии не могут пересекаться под ненулевым углом: в противном случае в точке пересечения напряженность была бы направлена сразу в две стороны, что абсурдно. Можно легко доказать, что силовые линии не могут и касаться друг друга. В вакууме электрические силовые линии начинаются и заканчиваются либо на заряженных телах, либо в бесконечности (см. рис. 4).
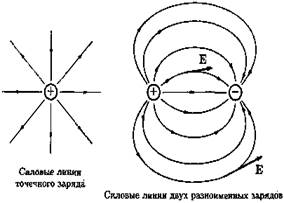
Рис. 4
Эквипотенциальной поверхностью называется такая поверхность, все точки которой обладают одним и тем же значением потенциала. Так же как и силовых линий, эквипотенциальных поверхностей может быть построено бесконечно много.
Так как все точки эквипотенциальной поверхности имеют одинаковый потенциал, перемещение заряда, по этой поверхности не требует работы (работа пропорциональна разности потенциалов). Но работа пропорциональна косинусу угла между перемещением и силой, поэтому сила, а значит и напряженность, всегда перпендикулярна к эквипотенциальной поверхности. Таким образом, эквипотенциальные поверхности всегда перпендикулярны силовым линиям (см.рис.5)
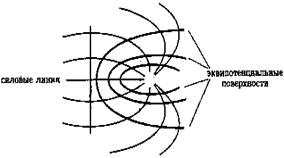
Рис. 5
1.5. Теорема Гаусса
Для напряженности электрического поля выполняется теорема Гаусса. Хотя мы покажем ее на основе закона Кулона, эта теорема справедлива в самом общем случае, т. е. для электрических полей любой природы, а не только электростатических.
Вначале определим новую величину. Потоком вектора напряженности электрического поля Е через поверхность S называется величина N, равная
где En — проекция вектора Е на направление нормали к поверхности. Эту формулу можно пояснить следующим образом.
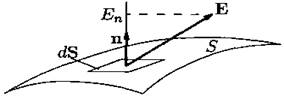
Рис. 6
Чтобы определить поток вектора напряженности через поверхность S (см. рис. 6), необходимо разбить эту поверхность на маленькие участки площадью dS; в пределах каждого такого участка можно считать, что вектор Е имеет одно и тоже значение. Определяется En — проекция вектора E на нормаль n . Площадь каждого участка умножается на En. Получившаяся величина Еn dS есть поток вектора dN через малый участок dS. Поток через поверхность S есть сумма всех таких Еn dS:
Эту формулу можно записать как
введя вектор dS = n × dS, величина которого равна площади dS, а направление совпадает с направлением единичного вектора нормали n.
Оказывается, поток вектора E через любую замкнутую поверхность определяется только суммарным зарядом, находящимся внутри нее (теорема Гаусса). Докажем ее.
Проведем вокруг точечного заряда Q сферу радиуса
, центр
которой совпадает с зарядом(см. рис. 7а). В каждой точке сферы вектор
напряженности по величине равен
и направлен перпендикулярно поверхности сферы. Следовательно, поток вектора напряженности через сферу есть
где
интегрирование производится по всей поверхности сферы. Очевидно, что последний
интеграл — это площадь поверхности сферы 
поэтому
поток через сферу равен
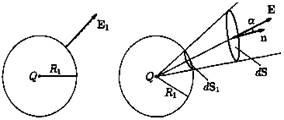
а) б)
Рис. 7
Пусть теперь заряд окружен произвольной поверхностью S и элемент ее dS выделяется тем же пучком линий, что и элемент первоначальной сферической поверхности (см. рис. 7б). Очевидно.
где R — расстояние от элемента поверхности dS до
заряда, 
— угол
между нормалью к dS и радиус-вектором R.
Поэтому
Поток вектора напряженности через элемент dS равен
т. е. точно равен потоку
через элемент 
.
Поэтому полный поток через всю произвольную замкнутую поверхность S
такой же, как и через сферическую поверхность, т. е. равен
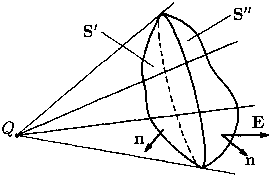
Рис. 8
Поток вектора напряженности от точечного заряда через замкнутую поверхность равен нулю, если заряд лежит вне этой поверхности. Действительно, пучок касательных, проведенных от заряда, делит поверхность на две части — S’ и S’’ (см. рис. 8). Потоки вектора E через эти поверхности равны по величине, но имеют разные знаки, поэтому полный поток равен нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.