Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 12

где  — скорость электрона в отсутствии внешнего поля. Средняя скорость электронов равна (угловые скобки означают усреднение)

где  — среднее время между столкновениями электрона с решеткой (коэффициент 1/2 появляется в результате усреднения, так как скорость, приобретаемая электроном под действием внешнего поля, линейно зависит от времени). Но <>) — средняя скорость электронов в начальный момент — равна нулю, поэтому средняя скорость электронов, находящихся в поле Е, равна:

*Средняя скорость, которую приобретают электроны в металле при обычных полях, не более нескольких миллиметров в секунду. Эта скорость не имеет отношения к скорости распространения электрического сигнала по проводнику (скорости света).

Теперь можно вычислить плотность тока:

Итак, плотность тока в каждой точке проводника пропорциональна напряженности поля в этой точке. Это соотношение называется законом Ома в дифференциальной форме.

Закон Ома в дифференциальной форме получен нами с использованием классической механики, которая неприменима для объяснения микроскопических свойств твердых тел, в частности не позволяет определить среднее время между столкновениями. Однако точные расчеты и эксперименты подтверждают, что плотность тока обычно пропорциональна напряженности поля:

Коэффициент пропорциональности  называется проводимостью.

Прямо пропорциональная зависимость между плотностью тока и напряженностью электрического поля с очень высокой точностью выполняется для металлов. Для других сред эта зависимость может быть более сложной.

Часто закон Ома в дифференциальной форме записывают в виде

   

где  — удельное сопротивление проводника. Удельное сопротивление проводника зависит от температуры t. Удельное сопротивление металлов линейно возрастает с увеличением температуры:

.

3.4. Закон Ома в интегральной форме. Сопротивление.

Закон Ома в дифференциальной форме устанавливает связь между плотностью тока и напряженностью поля в каждой точке проводника. Определим на основе этого закона ток через проводник. Будем для простоты считать, что плотность тока во всех точках одного и того же сечения проводника одинакова и равна силе тока, деленной на площадь сечения:

Закон Ома в дифференциальной форме запишем в виде

Проинтегрируем обе части этого выражения по длине проводника L, выразив плотность тока через ток и площадь сечения:

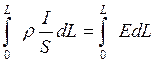
или

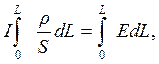
так как ток I — постоянный, следовательно, один и тот же по всей длине проводника. Интеграл

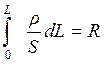
определяется только геометрией проводника и его удельным сопротивлением, он называется сопротивлением проводника. Нетрудно видеть, что если удельное сопротивление  и площадь сечения проводника S одинаковы по всей длине проводника, то сопротивление равно

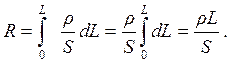
Интеграл от напряженности по длине проводника

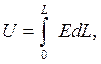
называется напряжением. Поэтому закон Ома в интегральной форме может быть сформулирован в следующем виде: произведение тока через проводник на сопротивление проводника равно напряжению на концах проводника

3.5. Напряжение. Электродвижущая сила.

В чисто электростатических полях постоянный ток течь не может. Однако, как мы знаем из опыта, постоянный ток возможен. Значит, могут существовать поля, в которых напряженность поля имеет не электростатическую природу. Напряженность таких полей, называемых сторонними, будем обозначать Естор. Очевидно, что напряженность общего электрического поля есть сумма напряженностей электростатического поля Еэ и Естор, поэтому напряжение между точками 1 и 2 проводника, равное

можно представить как сумму интегралов

Как известно из электростатики, первый из этих интегралов есть разность потенциалов между точками 1 и 2:

Интеграл от напряженности стороннего поля на участке между точками 1 и 2 проводника называется электродвижущей силой (ЭДС), действующей на этом участке проводника:

Очевидно, ЭДС численно равна работе, которую совершает стороннее (не электростатическое) поле по перемещению единичного заряда из точки 1 в точку 2.