Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 10

      

Но по определению емкости это есть отношение заряда к напряжению

откуда получаем, что емкость эквивалентного конденсатора при параллельном соединении равна

т. е. сумме емкостей.

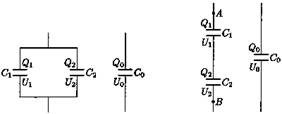
Рис. 17                                  Рис. 18

Последовательное соединение. Разность потенциалов между точками А и В (см. рис. 18) равна

где  и  — соответствующие разности потенциалов для каждого конденсатора. Выразив разность потенциалов на каждом конденсаторе через его емкость, получим

Заряды на обоих конденсаторах равны друг другу и заряду эквивалентного конденсатора:

откуда

2.9. Энергия конденсатора

Заряженный конденсатор обладает определенной энергией. Вычислим ее. Пусть конденсатор, первоначально заряженный до разности потенциалов U, разряжается, т. е. заряд с одной обкладки переходит на другую; разность потенциалов при этом конечно уменьшается.

Обозначим через U(t) значение разности потенциалов в момент времени t. Если при разряде малый заряд dQ(t) проходит между обкладками, работа равна произведению этого заряда на разность потенциалов между обкладками:

Но  в любой момент времени, поэтому

значит работа по перемещению малого заряда равна

Полная работа, совершаемая при разряде конденсатора от первоначального потенциала U до нулевого потенциала, равна интегралу

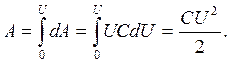
Очевидно, что эта работа равна энергии заряженного конденсатора.

Учитывая связь между емкостью, потенциалом и зарядом, выражение для энергии конденсатора можно записать в нескольких эквивалентных формах:

2.10. Энергия электрического поля

Подставив выражение для емкости плоского конденсатора

в формулу для его энергии

получим, что энергия равна

где D — электрическая индукция, Е — напряженность поля, V — объем между обкладками. Эта формула означает, что энергия конденсатора пропорциональна его объему, умноженному на

Такая форма записи не случайна:  есть плотность энергии электростатического поля. Энергия конденсатора заключена в поле внутри него. Эту интерпретацию о локализации энергии конденсатора нельзя получить в рамках электростатики. Однако электродинамика дает точный результат: плотность энергии электрического поля равна половине от скалярного произведения электрической индукции на напряженность электрического поля:

.

2.11. Емкость и энергия заряженного проводника

Емкость проводника определяется как отношение заряда на проводнике к его потенциалу:

(потенциал на бесконечности считается равным нулю). Энергия заряженного проводника подсчитывается точно так же, как и энергия конденсатора:

,

.

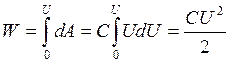2.12. Резюме

По своей способности проводить электрический ток все обычные вещества можно разделить на проводники, диэлектрики и полупроводники. Проводники могут проводить электрический ток, т. к. содержат свободные заряды, способные двигаться внутри проводника под действием поля. Напряженность поля и плотность заряда внутри однородного проводника, помещенного во внешнее электростатическое поле, равна нулю; потенциал всех точек проводника одинаков.

Диэлектрики не содержат свободных зарядов и не проводят электрический ток. Напряженность электрического поля внутри диэлектрика в  раз меньше, чем напряженность внешнего электростатического поля, если диэлектрик заполняет всю область между двумя эквипотенциальными поверхностями (- диэлектрическая проницаемость данного диэлектрика). Это объясняется тем, что под действием поля диэлектрик приобретает дипольный момент, зависящий от величины поля. Отношение этого дипольного момента в некотором объеме диэлектрика к величине этого объема называется поляризованностью Р.

Вектор электрической индукции равен

где  — напряженность поля внутри диэлектрика. Поток вектора электрической индукции через замкнутую поверхность равен сумме свободных зарядов, находящихся внутри этой поверхности (теорема Гаусса для электрической индукции):

Электрическое поле обладает энергией. Плотность энергии электрического поля равна

.