Векторы dl и j лежат на одной прямой, поэтому, учитывая, что ток I в проводнике равен произведению плотности тока на площадь сечения, получаем закон Ампера: сила, действующая на элемент dl провода, по которому течет ток I, равна силе тока, умноженной на векторное произведение dlи dВ:
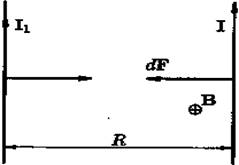
Рис. 34
Важный частный случай законе Ампера: если поле создается другим, параллельным данному проводом (см. рис. 34), в котором течет ток I1 , то создаваемая им магнитная индукция равна
и сила, действующая на ток I, равна по величине
(здесь R — расстояние между проводами). Применяя правило левой руки видим, что параллельно текущие токи притягиваются.
4.7. Контур с током в однородном магнитном поле
Рассмотрим механические воздействия, оказываемые однородным магнитным полем на замкнутый контур, по которому течет ток.
Момент сил, действующих на контур. Рассмотрим прямоугольный контур (см. рис. 35). Силы, действующие на стороны а, лежат в плоскости контура и стремятся либо растянуть, либо сжать контур, поэтому момент этих сил равен нулю. На каждую из сторон b действует сила F, которая в соответствии с законом Ампера равна F = IbB. Эти силы равны по величине и направлены в противоположные стороны. Они стремятся повернуть контур так, чтобы его плоскость стала перпендикулярна вектору
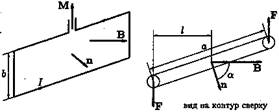
Рис. 35
магнитной индукции В. Следовательно, на контур действует пара сил, значит момент сил равен удвоенному произведению силы на плечо:
Но аb есть площадь контура S, поэтому величина момента сил может быть записана в виде
Момент М есть векторная величина. Момент направлен так, как указано на рисунке. Так как В тоже векторная величина, можно записать предыдущую формулу в виде
, где
вектор Р = ISn называется магнитным моментом
контура с током (вектор n
— нормаль к контуру; направление вектора п. и направление тока в контуре
связаны правилом буравчика).
Итак, момент сил, действующий на находящийся в магнитном поле замкнутый контур, равен
Можно легко доказать, что эта формула справедлива не только для прямоугольного контура, но и для контура произвольной формы. Для этого нужно разбить произвольный контур на прямоугольные контуры, определить момент сил, действующий на каждый из них, и вычислить суммарный момент сил
4.8. Магнитное поле в веществе
Если поместить вещество в магнитное поле с определенным значением магнитной индукции, то магнитная индукция внутри вещества будет отличаться от этого значения. Упрощенно это объясняется тем, что вследствие вращения электронов вокруг ядра каждый атом является маленьким витком с током, поэтому каждый атом может обладать отличным от нуля магнитным моментом. Под действием внешнего магнитного поля магнитные моменты атомов определенным образом ориентируются, что приводит к появлению дополнительного магнитного поля. Суммарный магнитный момент I единицы объема вещества называется вектором намагничивания или намагниченностью.
Пусть магнитное поле создается некоторым током I. Если в это поле поместить вещество, то теорема о циркуляции вектора магнитной индукции по произвольному контуру (см. рис. 36) записывается в виде
Здесь Im — токи, обусловленные внутриатомным движением;
Рис. 36
S(1m ) = 1м — сумма этих токов, пронизывающих поверхность, натянутую на контур интегрирования. Так как магнитные моменты атомов ориентируются под действием магнитного поля, то эта сумма не равна нулю. Эта сумма называется током намагничивания Iм, токи Im, обусловленные внутриатомным движением, называют микротоками.
Выразим ток намагничивания 1м через вектор намагничивания I. Элемент контура ей нанизывает на себя только те микровитки с током, центры которых попадают внутрь изображенного на рисунке 36 косого цилиндра с объемом
где Sm — площадь каждого микровитка, а — угол между нормалью к плоскости микровитка п и вектором dl. В соответствии с теоремой о циркуляции все остальные микровитки не влияют на величину циркуляции вектора В.
Суммарный микроток, охватываемый элементом контура dl,
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.