Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 22

Разность потенциалов между обкладками конденсатора, подключенного к изменяющейся по гармоническому закону ЭДС (см. рис. 43), равна

Но эта разность потенциалов пропорциональна имеющемуся в данный момент заряду конденсатора Q(t) и обратно пропорциональна его емкости С:

Заряд Q(t) равен интегралу от тока

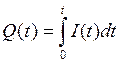
Подставляя этот интеграл вместо Q(t), получаем

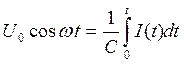
Продифференцировав это соотношение, находим выражение для силы тока через конденсатор, подключенный к изменяющейся по гармоническому закону ЭДС:

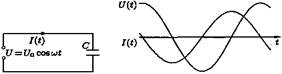
Рис.43                                                                     Рис.44

Ток через конденсатор на π/2 опережает по фазе напряжение (см. рис. 44). Сила тока обратно пропорциональна величине

которая может трактоваться как эффективное сопротивление емкости в цепи переменного тока.

5.9. Индуктивность в цепи переменного тока

По закону Ома сумма ЭДС в замкнутом неразветвленном контуре равна произведению тока на активное сопротивление контура, которое равно нулю для приведенной на рисунке 45 схемы. Поэтому

Так как ЭДС индукции обусловлена явлением самоиндукции, она равна

Подставляя это в предыдущую формулу, находим производную тока через индуктивность

Проинтегрировав, получаем зависимость тока через индуктивность от времени

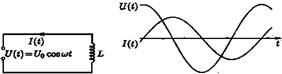
Рис.45                                                           Рис.46

Ток через индуктивность на π/2  отстает по фазе от напряжения на ней (см. рис. 46). Сила тока обратно пропорциональна величине

которую можно рассматривать как эффективное сопротивление индуктивности в цепи переменного тока.

7. Движение заряженных частиц

7.1. Свободная частица в однородном магнитном поле

Если частица движется в однородном магнитном поле с индукцией В, а напряженность электрического поля равна нулю, то на частицу с зарядом  действует сила

всегда направленная перпендикулярно скорости частицы v. Будем рассматривать движение только со скоростями, малыми по сравнению со скоростью света, т. е. пренебрежем эффектами теории относительности. По второму закону Ньютона ускорение частицы направлено по вектору силы и равно

Так как сила F перпендикулярна скорости, она не совершает работы, значит кинетическая энергия частицы не изменяется, т. е. скорость частицы остается постоянной по величине, изменяясь лишь по направлению.

1) Рассмотрим сначала случай, когда скорость частицы перпендикулярна вектору магнитной индукции В. При этом ускорение частицы по абсолютной величине равно

и направлено перпендикулярно скорости. Из механики известно, что при этом частица движется по окружности. Приравнивая ускорение частицы в магнитном поле к величине центростремительного ускорения

получаем, что частица движется по окружности радиуса

Время, затрачиваемое на один оборот (период обращения) равно

т. е. период обращения не зависит от скорости частицы. Так как частота обращения v (количество оборотов в единицу времени) есть — она также не зависит от скорости, а определяется величиной магнитной индукции и отношением заряда частицы к ее массе:

2) Пусть теперь угол между скоростью частицы и магнитной индукцией отличается от прямого. Разложим скорость частицы на две составляющие - перпендикулярную вектору магнитной индукции v1 и параллельную этому вектору v2. Сила Лоренца равна F = e[v,B] = e[(v1 + v2), b] = e[v1,B] + e[v2, B]. Последнее слагаемое равно нулю в силу свойств векторного произведения. Это значит, что в направлении, параллельном вектору В, на частицу никакие силы не действуют. Следовательно, по этому направлению она движется с постоянной скоростью.

В плоскости, перпендикулярной вектору В, частица движется по окружности, радиус которой равен

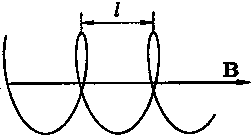
Итак, движение частицы есть наложение движений по окружности определенного радиуса и прямолинейного движения, т. е. частица движется по винтовой линии (спирали - см. рис. 52. Период обращения равен

шаг (расстояние между соседними витками спирали)