Для наглядного изображения магнитного поля часто рисуют магнитные силовые линии — линии, касательные к которым в каждой точке совпадают с направлением магнитной индукции (см. рис. 30). Силовые линии магнитного поля, создаваемого постоянными токами, замкнуты.
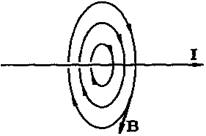
Рис. 30
4.4. Циркуляция магнитной индукции
Циркуляцией магнитной индукции В по замкнутому контуру называется интеграл
![]()
Оказывается,
что этот интеграл прямо зависит от величины суммарного тока, пронизывающего
поверхность, натянутую на контур. Если магнитное поле создается только токами,
то циркуляция равна умноженной на ![]() сумме токов,
пронизывающих любую поверхность, натянутую на этот контур:
сумме токов,
пронизывающих любую поверхность, натянутую на этот контур:
![]()
Докажем это для бесконечных прямых токов. Рассмотрим сначала прямой ток и контур в виде окружности радиуса Rо (см. рис. 31), центр которой совпадает с проводом, и перпендикулярной проводу. Очевидно, что в каждой точке выбранного нами контура векторы Во и dlпараллельны, поэтому
![]()
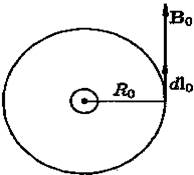
Рис. 31
Но магнитная индукция прямого тока равна
![]()
поэтому циркуляция равна
![]()
Интеграл fdlo есть просто длина окружности 2тгRо, поэтому циркуляция вектора магнитной индукции по окружности равна
![]()
Теперь рассмотрим контур, произвольная часть которого отличается от окружности, но ток остается внутри контура (см. рис. 32).
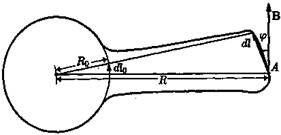
Рис. 32
Очевидно, что длина элемента dl связана с длиной соответствующего элемента окружности соотношением
![]()
откуда
![]()
Магнитная индукция в точке А равна по модулю
![]()
и составляет угол if с вектором dl. Поэтому
![]()
Мы получили, что для любого элемента «не окружности» величина В dl равна В0 dl0 для окружности, откуда следует, что циркуляция магнитной индукции для «не окружности» такая же, как и для окружности:
![]()
Если контур 7 пронизывается не одним, а несколькими токами, то в силу принципа суперпозиции на равных правах должен учитываться каждый из этих токов. Значит, циркуляция вектора магнитной индукции должна определяться суммой токов, охватываемых контуром интегрирования:
![]()
Теорема о циркуляции магнитной индукции доказана для бесконечных прямых токов. Можно доказать, что она справедлива для токов любой формы.
4.5. Магнитное поле тороидальной катушки и соленоида
Применим теорему о циркуляции магнитной индукции к тороидальной катушке (проводу с током, намотанному на тор, см. рис. ЗЗа). Проведем окружность радиуса R, лежащую внутри тороида. Если витки катушки плотно прилегают друг к другу, магнитную индукцию во всех точках выбранной окружности можно считать одинаковой и направленной по касательной к ней. Поэтому циркуляция магнитной индукции равна в этом случае произведению модуля вектора В на длину окружности:
![]()
Но по теореме о циркуляции она равна произведению mо на сумму токов, пронизывающих поверхность, натянутую на выбранную окружность:
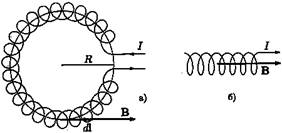
Рис. 33
![]()
где N — полное число витков катушки; отсюда находим магнитную индукцию внутри катушки:
![]()
Если радиус R очень большой по сравнению с радиусом витка, то любой не очень протяженный отрезок катушки является просто прямой катушкой (соленоидом, см. рис. 33б). Замечая, что
![]()
есть количество витков, приходящееся на единицу длины соленоида, получаем, что магнитная индукция внутри соленоида равна
![]()
где I — ток, текущий по проводу. Конечно, вектор В направлен по оси соленоида.
4.6. Действие магнитного поля на ток. Закон Ампера
Ток, текущий в проводнике, обусловлен движением зарядов. На каждый движущийся заряд действует сила Лоренца. Поэтому на проводник с током действует сила, равная сумме сил Лоренца, действующих на каждый заряд. Вычислим эту суммарную силу. На элемент провода dl действует сила, равная
![]()
где е — заряд каждого носителя тока,
Vcp = <v>,— средняя скорость носителей тока,
dN = nSdl — количество носителей тока в элементе провода длиной dl и сечением S,
п — концентрация носителей тока в проводнике.
Подставляя выражение для dN в формулу для силы, получаем
![]()
В круглых скобках — вектор плотности тока j, значит
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.