Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 3

Как доказывается в курсе математики, эта формула эквивалентна тому, что напряженность есть градиент от потенциала (со знаком минус):

В одномерном случае, т. е. если напряженность поля во всех точках координатной оси направлена по этой оси, связь между напряженностью и потенциалом принимает простой вид

Зная потенциал в каждой точке пространства, по этим формулам можно найти напряженность в каждой точке, и наоборот. Это означает, что электростатическое поле можно описать двумя эквивалентными способами: либо задавая в каждой точке пространства напряженность (вектор), либо потенциал (скаляр).

Потенциал φ можно определить как отношение потенциальной энергии, которой обладает заряд в электростатическом поле, к величине этого заряда q. Если заряд переместится из точки с потенциалом φ₁ в точку с потенциалом φ₂, то его потенциальная энергия увеличится на        q(φ₂-φ₁).Полная энергия сохраняется, поэтому это приводит к соответствующему изменению других видов энергии (например, к изменению кинетической энергии заряда, либо, если заряд взаимодействует с другими телами, к изменению их энергии).

Связь между напряженностью и потенциалом такая же, как и связь между силой и потенциальной энергией. При изучении механики подробно объяснялось, что потенциальная энергия определена с точностью до произвольной постоянной, так как имеет смысл говорить только о разности потенциальных энергий между двумя точками пространства. Аналогично обстоит дело и с потенциалом. Потенциал определен с точностью до постоянной величины, одинаковой для всех точек пространства. Если к потенциалу каждой точки пространства прибавить любую одну и ту же величину (положительную или отрицательную), работа по перемещению заряда из одной точки пространства в другую, пропорциональная разности потенциалов этих точек, не изменится. Однако часто говорят просто о потенциале в данной точке. При этом всегда подразумевают, что потенциал в какой-то точке имеет определенное значение. Часто (но не всегда) считают, что потенциал в бесконечно удаленной точке равен нулю.

Если результирующее поле образовано наложением нескольких полей, то результирующая напряженность равна векторной сумме напряженностей каждого поля:

E=E₍₁₎ +E₍₂₎+…

Пусть в точке 2 потенциал выбран равным нулю. Тогда из очевидных равенств

следует, что потенциал в произвольной точке равен сумме потенциалов всех полей, образующих результирующее поле. Конечно, это прямое следствие принципа суперпозиции.

Докажем, что электростатическое поле потенциально, т. е. разность потенциалов между точками 1 и 2 не зависит от траектории, по которой происходит перемещение заряда из точки 1 в точку 2. Пусть поле создается только одним точечным зарядом Q. Тогда по определению разности потенциалов

Скалярное произведение г dr= |г| × |dr| × cos а равно r×dr — произведению расстояния r до заряда на приращение этого расстояния dr (см. рисунок 3). Заменяя r dr на r dr, получаем

Это означает, что разность потенциалов зависит только от расстояний r₁ и r₂, на которых точки 1 и 2 находятся от заряда Q, и не зависит от траектории, по которой происходит перемещения заряда q из точки 1 в точку 2.

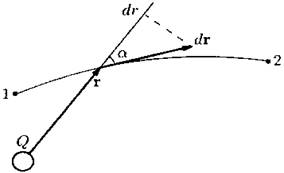
Рис. 3

Потенциальность электростатического поля доказана для одного точечного заряда, но из принципа суперпозиции с очевидностью следует потенциальность электростатического поля для любой произвольной системы неподвижных зарядов.

В курсе механики доказывалось, что утверждение о независимости работы от траектории эквивалентно утверждению о том, что работа по замкнутому контуру равна нулю. Совершенно аналогично из независимости разности потенциалов от траектории следует, что интеграл по замкнутому контуру от напряженности электростатического поля равен нулю:

Необходимо подчеркнуть, что равенство нулю интеграла от напряженности по замкнутому контуру доказано с использованием закона Кулона, т. е. для полей, создаваемых неподвижными зарядами. Для неэлектростатических полей это утверждение становится неверным.