Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 8

Эксперименты и расчеты показывают, что для многих случаев (а другие мы рассматривать не будем) поляризованность Р диэлектрика пропорциональна напряженности поля  внутри диэлектрика:

P = χε₀E_{вн ,}

где  — коэффициент пропорциональности, зависящим от диэлектрика и называемый диэлектрической восприимчивостью. Здесь и в дальнейшем под напряженностью поля внутри диэлектрика E_вн и аналогичными величинами мы будем понимать напряженность, усредненную по малому, но содержащему много атомов объему вещества, не интересуясь микроскопическими вариациями напряженности, связанными с молекулярным строениями вещества.

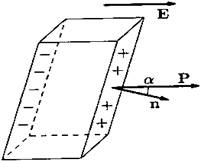
Рис. 13

Определим связь между поверхностной плотностью поляризационных зарядов  и поляризованностью Р. Пусть диэлектрик в форме призмы с ребром L и площадью основания S находится в однородном внешнем поле напряженностью Е. Вектор поляризованности Р направлен так же, как и вектор Е и в общем случае составляет угол а с нормалью к поверхности призмы.

Дипольный момент R всей призмы равен по модулю произведению величины поляризационного заряда на длину призмы L (см. рис. 13):

.

Но дипольный момент всей призмы есть произведение объема призмы на дипольный момент единицы объема, т. е. на поляризованность:

Приравнивая, получаем

 

откуда

_.

Здесь Р_n — проекция вектора Р на нормаль n.

Итак, поверхностная плотность поляризационного заряда диэлектрика, находящегося в электрическом поле, равна нормальной составляющей его поляризованности. Учитывая связь между Р и

P = χε₀E_{вн ,}

получаем связь между поверхностной плотностью поляризационного заряда и полем внутри диэлектрика:

= χε₀E_вн cos.

2.4. Напряженность поля внутри диэлектрика.

Пусть диэлектрик в виде бесконечного плоского слоя расположен в однородном электрическом поле так, что его поверхность перпендикулярна вектору Е; другими словами, диэлектрик в точности заполняет область между двумя эквипотенциальными поверхностями однородного поля.

На верхней и нижней поверхности диэлектрика образуются поверхностные поляризационные заряды с плотностью а. Выделим цилиндрическую поверхность, ось которой параллельна вектору Е (см. рис. 14), и применим к ней теорему Гаусса. Поток вектора Е через эту поверхность складывается из потоков через верхнее и нижнее «донышко» (эти потоки, разумеется, имеют разные знаки):

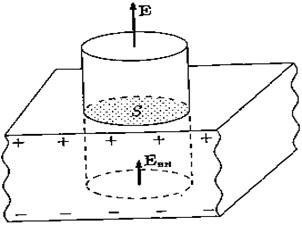
Рис. 14

По теореме Гаусса этот поток равен деленному на  суммарному заряду, находящемуся внутри цилиндрической поверхности, т. е.

Приравнивая, получаем

Учитывая установленную ранее связь между плотностью поляризационного заряда и напряженностью поля внутри диэлектрика, которая в данном случае имеет вид

= χε₀E_вн , получаем

χE_вн=E-E_вн,

откуда выражаем напряженность поля внутри диэлектрика через напряженность внешнего поля:

.

Здесь буквой  обозначена величина 1+.Эта величина называется диэлектрической проницаемостью и ее численное значение зависит от диэлектрика.

Мы вычислили напряженность поля внутри диэлектрика в частном случае. Можно доказать следующий общий результат. Напряженность поля внутри диэлектрика в любой его точке в  раз меньше, чем в отсутствии диэлектрика, если диэлектрик заполняет всю область между двумя эквипотенциальными поверхностями (если это условие несправедливо, то напряженность рассчитывается гораздо более сложным образом). В частности, если все пространство заполнено диэлектриком, то напряженность поля в  раз меньше, чем была бы в вакууме.

2.5. Вектор электрической индукции и теорема Гаусса для него.

При применении теоремы Гаусса к вектору Е необходимо учитывать все заряды, свободные и поляризационные, находящиеся внутри замкнутой поверхности S:

Вычисление по этой теореме вектора Е для диэлектрика произвольной формы неудобно. Дело в том, что входящий в правую часть поляризационный заряд зависит от того самого поля, напряженность которого нужно найти, от формы диэлектрика и от выбора поверхности S.

Можно доказать, что для вектораD, который по определению равен