Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 15

Количество теплоты, выделяющейся на сопротивлении за время t₀, равно

Если ток постоянный, то

(закон Джоуля-Ленца).

При последовательном соединении двух проводников эквивалентное сопротивление равно

при параллельном соединении.

4. Магнитное поле

4.1. Магнитная индукция. Сила Лоренца

Есть еще одна сила, которая может действовать на обладающую зарядом частицу. Эту силу удобно описать, введя понятие магнитного поля. Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией В. Это название закрепилось за величиной В по историческим причинам. Более логичным было бы назвать эту величину напряженностью магнитного поля. Для магнитной индукции, так же как и для напряженности электрического поля, выполняется принцип суперпозиции — суммарная магнитная индукция в некоторой точке пространства есть векторная сумма магнитных индукций отдельных полей.

Магнитное поле действует только на движущуюся частицу. Сила, обусловленная магнитным полем, пропорциональна заряду частицы и векторному произведению скорости частицы v на магнитную индукцию В:

Если имеется еще и электрическое поле с напряженностью Е, то общая сила, действующая на частицу, равна

Эта сила называется силой Лоренца, однако в большинстве случаев силой Лоренца называют только силу, обусловленную магнитным полем, т.е. определяемую формулой . Сила Лоренца действует только на движущийся заряд. Ее направление перпендикулярно направлению скорости, направлению магнитной индукции и определяется правилом левой руки (см. рис. 27).

4.2. Закон Био-Савара-Лапласа

Откуда берется магнитное поле? Оказывается, оно может создаваться электрическим током. Соотношение, позволяющее в любой точке пространства вычислить величину магнитной индукции, создаваемой любым постоянным током, называется законом Био-Савара-Лапласа.

Рассмотрим произвольный тонкий провод, по которому течет ток I. Разобьем этот провод на бесконечно маленькие направленные отрезкиdl. Закон Био-Савара-Лапласа заключается в следующем: магнитная индукция dB, создаваемая в произвольной

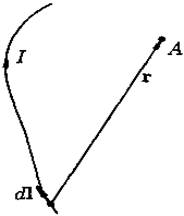
Рис. 28

точке А элементом провода dl (см. рис. 28), по которому течет ток I, равна

гдеr — радиус-вектор, проведенный от элемента токаdl к этой точке. Коэффициент пропорциональности  численно равен

Вектор магнитной индукцииdB перпендикулярен вектору dl и векторуr. Для определения направления вектора магнитной индукции полезно использовать правило буравчика: направление вектора магнитной индукции совпадает с направлением конца рукоятки буравчика, ввинчиваемого в направлении тока.

Для того, чтобы подсчитать магнитную индукцию, создаваемую всем проводом с током, нужно просуммировать магнитные индукции, создаваемые каждым элементом тока. Если есть несколько проводов с током, то результирующая магнитная индукция в точке А равна сумме магнитных индукций, создаваемых каждым из них.

4.3. Магнитная индукция бесконечного прямого тока

Используя закон Био-Савара-Лапласа, найдем магнитную индукцию, создаваемую в любой точке пространства бесконечным прямым проводом, по которому течет ток I. Магнитная индукция, создаваемая произвольным элементом тока dl в точке А (см. рис. 29), направлена перпендикулярно плоскости рисунка и по абсолютной величине равна

Длина отрезка dl связана с длиной радиус-вектора r соотношением 

где da — угол, под которым отрезок dl виден из произвольной точки А;

длина вектора г связана с расстоянием R от точки А до провода соотношением

Подставив два последних соотношения в закон Био-Савара-Лапласа, получаем

Для того, чтобы определить магнитную индукцию, создаваемую всем прямым проводом с током, необходимо учесть вклад всего провода, т. е. проинтегрировать это выражение по углу (в пределах от  -/2 до  +/2):

Итак, магнитная индукция, создаваемая бесконечным прямым проводом с током, прямо пропорциональна силе тока и обратно пропорциональна расстоянию до провода: