Рассмотрим теперь замкнутый проводник произвольной формы, находящийся в произвольном магнитном поле. Разобьем замкнутый проводник на бесконечно малые прямолинейные участки. При малом перемещении каждого этого участка магнитное поле можно считать постоянным, поэтому справедливо полученное выше выражение для ЭДС индукции. Если просуммировать эти ЭДС по всему замкнутому контуру, получаем закон электромагнитной индукции: ЭДС индукции в замкнутом контуре равна производной по времени от магнитного потока через этот контур со знаком «минус» (закон Фарадея):
ЭДС индукции возникает при любом изменении со временем магнитного потока через контур, например если контур неподвижен, а магнитное поле изменяется либо по величине, либо по направлению, либо одновременно по направлению и по величине.
5.4. Взаимная индукция
Явление электромагнитной индукции — это возникновение тока в замкнутом контуре, если изменяется магнитный поток через контур. Магнитный поток может создаваться током, текущим в другом проводнике, и изменяться при изменении этого тока. Взаимной индукцией называется возникновение ЭДС индукции в одном контуре при изменении тока в другом.
Очевидно, что магнитный поток, создаваемый в контуре 1 током, текущем в контуре 2, пропорционален току в контуре 2:
Коэффициент
пропорциональности
называется
коэффициентом взаимной индукции. Этот коэффициент зависит от геометрии обоих
контуров и их взаимного расположения. Можно доказать, что 
—
поток, создаваемый током в контуре 2 под действием тока в контуре 1, связан с
величиной тока 
точно таким
же по величине коэффициентом пропорциональности.
5.5. Самоиндукция. Индуктивность
ЭДС индукции возникает всегда, когда изменяется проходящий через контур магнитный поток. В частности, этот магнитный поток может создаваться тем самым током, который течет в контуре. Поэтому при всяком изменении тока в контуре в нем возникает ЭДС индукции, приводящая к дополнительному изменению тока.
Очевидно, что величина магнитного потока Ф через контур, создаваемого самим текущим через контур током I, пропорциональна величине этого тока:
Коэффициент пропорциональности L называется коэффициентом самоиндукции или индуктивностью. Единица измерения индуктивности — Генри. Индуктивность контура определяется его геометрией и магнитной проницаемостью заполняющего контур вещества; индуктивность не зависит от силы тока, если от силы тока не зависит геометрия контура и магнитная проницаемость.
5.6. Индуктивность соленоида
Большой величиной индуктивности обладает соленоид. Для| ее расчета используем полученную в параграфе 4.5 формулу для величины магнитной индукции внутри незаполненного веществом соленоида:
где N — число витков соленоида, I — его длина, I — сила, тока в соленоиде.
Магнитный поток через один виток равен
где S — площадь витка соленоида, а полный поток через все витки в N раз больше потока через один виток:
откуда индуктивность соленоида (отношение магнитного потока к току) равна
Если же соленоид полностью заполнен веществом с магнитной проницаемостью р,, то индуктивность соленоида в р, раз больше:
5.7. Переменный ток. Сопротивление в цепи переменного тока
В промышленности и в быту широко используется переменный синусоидальный ток:
с циклической частотой v = 50 Гц. Очевидно, круговая частота w у такого тока равна 314 c-1. Переменный гармонический ток создается ЭДС, изменяющейся со временем с той же частотой. Если размеры электрической цепи переменного тока не слишком велики (менее 104 метра), можно считать, что с точностью до одного процента ток во всех точках цепи пропорционален действующей в данный момент ЭДС.
Рассмотрим сопротивление (см. рис. 42), подключенное к ЭДС, изменяющейся со временем по закону
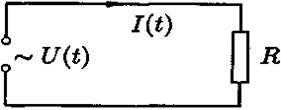
Рис. 42
В каждый момент времени выполняется закон Ома
откуда находим зависимость тока в цепи от времени:
5.8. Емкость в цепи переменного тока
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.