Заряд и поле. Электростатика в вакууме. Закон Кулона. Напряженность электрического поля. Потенциал, страница 11

Напряженность электрического поля внутри плоского конденсатора пропорциональна заряду конденсатора и обратно пропорциональна площади обкладки

Емкость конденсатора равна отношению заряда конденсатора к напряжению конденсатора:

и для плоского конденсатора равна

где d– расстояние между обкладками.

При параллельном соединении двух конденсаторов результирующая емкость равна их сумме,

а при последовательном определяется по формуле

 или

Энергия заряженного конденсатора

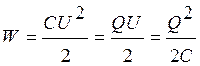
3. Постоянный электрический ток

3.1. Сила тока и плотность тока

Ток в проводнике возникает вследствие движения заряженных частиц. Сила тока равна производной по времени от суммарного заряда Q(t), прошедшего через поперечное сечение проводника к моменту времени t:

Единица измерения силы тока — Ампер.

Наряду с силой тока (часто силу тока называют просто током) важное значение имеет плотность тока. Средняя по сечению плотность тока равна отношению силы тока I к площади сечения проводника S:

Однако в общем случае плотность тока может быть разной в разных точках сечения. В этом случае ток равен интегралу от плотности тока по сечению.

3.2. Вектор плотности тока

Очевидно, что плотность тока связана со средней скоростью носителей заряда в данной точке сечения. Скорость — векторная величина, и плотность тока также характеризуется вектором; этот вектор является обобщением понятия плотности тока и называется вектором плотности тока. Если в проводнике заряженные частицы имеют концентрацию п, заряд е и среднюю скорость, то вектор плотности тока равен

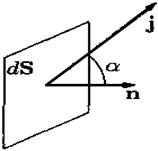
Рис. 19

.

Выделим внутри проводника малую площадку dS (см. рис. 19). Заряд, прошедший через нее за время dt, равен

где  — угол между jи нормалью к элементу поверхности dS.

Заряд, прошедший за время dt через все поперечное сечение проводника, равен сумме dq по всем точкам сечения, т. е. равен

Поделив обе части этого выражения на dt, получим связь между током в проводнике, равным по определению dQ/dt, и абсолютной величиной плотности тока в каждой точке сечения:

С помощью этого соотношения и учитывая приведенное выше выражение для вектора плотности тока, можно вычислить ток, если известны заряд носителей, их концентрация и средняя скорость:

Данная формула имеет общий характер. Из нее следует, что сила тока зависит и от направления. В частности, сила тока равна нулю в направлении, перпендикулярном направлению движения носителей заряда (т.к. cos 90° = 0). В дальнейшем мы практически всегда будем рассматривать ток в направлении, совпадающем с направлением средней скорости носителей.

3.3. Закон Ома в дифференциальной форме.

Сила тока в проводнике определяется средней скоростью носителей заряда. Если нет внешнего поля, то заряженные частицы движутся хаотически и вектор средней скорости хаотического движения носителей заряда  равен нулю, значит равна нулю и абсолютная величина этого вектора (|| = 0). Но скорость каждого заряда отлична от нуля, поэтому средняя абсолютная величина скорости электронов  не равна нулю. При комнатной температуре она обычно составляет несколько километров в секунду.

Важнейшими проводниками являются металлы. Их структуру можно приближенно представить как жестко связанные между собой ионы, образующие кристаллическую решетку, и движущиеся между ионами решетки электроны. В отсутствии внешнего поля электроны движутся хаотично и их средняя скорость равна нулю.

Рассчитаем, чему равна средняя скорость электронов в поле с напряженностью Е. Обозначим эту скорость  Предположим, что после каждого столкновения с решеткой электрон отдает ей всю энергию, полученную от электрического поля. Начало отсчета времени выберем в момент одного из столкновений электрона с решеткой. На электрон действует сила

(знак «минус» стоит потому, что заряд электрона е - отрицательный).

Из второго закона Ньютона

следует, что ускорение электрона равно

Поэтому скорость электрона во все моменты времени после столкновения и до следующего столкновения равна