По своим магнитным свойствам вещества делятся на диа-, пара- и ферромагнетики. У диамагнетиков магнитная проницаемость немного меньше единицы, у парамагнетиков немного больше. Магнитная проницаемость ферромагнетиков зависит от приложенного магнитного поля и может достигать больших значений. В ферромагнетиках наблюдается гистерезис — зависимость величины магнитной индукции от предыдущего состояния намагниченности.
5. Электромагнитная индукция
5.1. Магнитный поток
Потоком вектора магнитной индукции (или магнитным потоком) через охватываемую контуром γ поверхность S называется интеграл
![]()
где S — площадь поверхности, В — магнитная индукция, n — нормаль к поверхности, а — угол между векторами В и п. Это определение совершенно аналогично определению потока вектора напряженности электрического поля (см. параграф 1.5). Единицей магнитного потока является Вебер.
Величина магнитного потока зависит только от положения и формы контура 7 и имеет одинаковое значение для всех поверхностей, опирающихся на данный контур.
В простейшем случае, если контур γ плоский и поле однородно, магнитный поток равен произведению магнитной индукции на площадь контура и на косинус угла между векторами
![]()
Если хотя бы одна из этих величин зависит от времени, то магнитный поток также зависит от времени.
5.2. Работа при перемещении контура в магнитном поле
Пусть имеется контур, одна сторона которого представляет собой движущуюся перемычку (см. рис. 40). Магнитное поле однородно и направлено перпендикулярно плоскости рисунка. По закону Ампера на подвижную перемычку действует сила
![]()
где I — сила тока, I — длина перемычки, В — магнитная индукция. Если перемычку переместить на расстояние dx, совершится работа
![]()
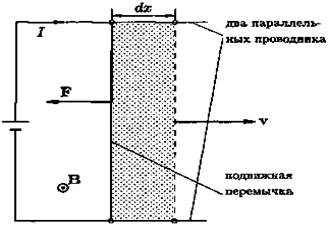
Рис. 40
или
![]()
Величина Idx — это заштрихованная на рисунке площадь, значит В1 dx есть магнитный поток, проходящий через заштрихованную площадь. Поэтому работа по перемещению перемычки на расстояние dx равна произведению тока на изменение магнитного потока:
![]()
Проинтегрировав это выражение, получаем
![]()
т. е. работа, совершаемая магнитным полем равна произведению тока (если ток постоянный!) на изменение магнитного потока через контур. Этот результат справедлив для любой ориентации магнитной индукции, т. к. работу совершает только та составляющая поля, которая перпендикулярна плоскости чертежа. Результат справедлив и для контура любой формы, т. к. его можно разбить на бесконечно малые элементы.
5.3. Электромагнитная индукция
Электрический ток создает вокруг себя магнитное поле. Существует ли обратное явление, т. е. вызывает ли магнитное поле электрический ток? Оказывается, ток создается только при каких-то изменениях либо магнитного поля, либо геометрии находящихся в нем проводников.
Пусть прямолинейный проводник длиной I движется со скоростью v в магнитном поле с индукцией В (см. рис. 41). На свободные носители проводника действует сила Лоренца, равная
![]() .
.
Если силу F разделить на величину заряда, получим напряженность стороннего поля Ест (т. к. напряженность этого поля имеет не электростатическую природу):
![]()
По определению электродвижущей силы, она раина интегралу от напряженности стороннего электрического поля по длине на участке MN:
![]()
(знак «минус» стоит потому, что вектор Ест направлен против обхода контура MNN1M1 от точки М к N и далее, определяемого правилом буравчика, а именно это направление принято за положительное).
Преобразуя последнюю формулу, получаем
![]()
где Ф(t) — «заметаемый» проводником за время t магнитный поток.
Рассчитаем, чему равна разность потенциалов на концах рассмотренного выше движущегося в магнитном поле проводника. Так как проводник незамкнутый, ток в нем равен нулю, а значит и произведение IR равно нулю. Применим к проводнику закон Ома:
![]()
![]()
Мы
получили, что при движении проводника в магнитном поле на его концах возникает
разность потенциалов, равная ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.