где
ε0 = 8,85·10-12. Данная формула устанавливает и
величину коэффициента пропорциональности, и направление силы, так как вектор ![]() есть
единичный вектор, совпадающий по направлению с радиус-вектором г,
проведенным от заряда Q к заряду q. Из этой формулы видно, что
если оба заряда имеют одинаковые знаки, то они отталкиваются (знак силы
взаимодействия такой же, как у радиус-вектора, т.е. она направлена по
радиус-вектору), а если разные знаки — притягиваются (сила направлена противоположно
направлению радиус-вектора). Силы, действующие на заряды Q и q, равны по
величине, противоположны по направлению и лежат на одной прямой (см. рис. 1).
есть
единичный вектор, совпадающий по направлению с радиус-вектором г,
проведенным от заряда Q к заряду q. Из этой формулы видно, что
если оба заряда имеют одинаковые знаки, то они отталкиваются (знак силы
взаимодействия такой же, как у радиус-вектора, т.е. она направлена по
радиус-вектору), а если разные знаки — притягиваются (сила направлена противоположно
направлению радиус-вектора). Силы, действующие на заряды Q и q, равны по
величине, противоположны по направлению и лежат на одной прямой (см. рис. 1).
![]()
Рис. 1
Строго
говоря, закон Кулона абсолютно верен лишь для зарядов, которые все время
неподвижны. Однако этот закон справедлив с очень высокой степенью точности,
если заряды движутся не слишком быстро и находятся не очень далеко друг от
друга. Когда имеются только два взаимодействующих заряда, законом Кулона можно
пользоваться, если скорости зарядов υ много меньше скорости света с.
Если же поле, действующее на заряд q, создается системой зарядов, имеющей
характерный размер l,
условие применимости закона Кулона имеет вид ![]() , где r — расстояние от системы зарядов до заряда q.
Кроме того, ускорения зарядов должны быть не слишком велики.
, где r — расстояние от системы зарядов до заряда q.
Кроме того, ускорения зарядов должны быть не слишком велики.
1.2. Напряженность электрического поля
Введем теперь понятие напряженности электрического поля. Напряженностью электрического поля Е называется отношение силы, действующей на неподвижный электрический заряд q, к величине этого заряда:
![]()
Напряженность — векторная величина. Размерность напряженности Вольт/метр. Используя определение напряженности, закон Кулона можно сформулировать так: неподвижный точечный заряд Q создает в каждой точке пространства вокруг себя электрическое поле с напряженностью, равной
![]() ,
,
где г — радиус-вектор, проведенный от заряда Q в эту точку. Выражая силу через напряженность, получаем, что сила, действующая на зарядq, находящийся в поле, создаваемом зарядом
![]() .
.
Это выражение полностью совпадает с законом Кулона, сформулированным ранее.
Если имеется несколько зарядов, например Q1 и Q2; то, согласно принципу суперпозиции, напряженность результирующего электрического поля есть векторная сумма напряженностей, создаваемых каждым отдельным зарядом: E=E1+E2 (рис. 2).
Таким образом, для того, чтобы подсчитать силу, действующую на какой-либо заряд q, находящийся в определенной точке
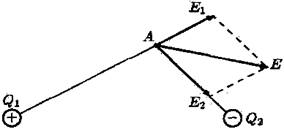
Рис. 2
А, нужно определить напряженности полей, создаваемых в этой точке каждым другим зарядом, найти векторную сумму этих напряженностей и умножить полученную результирующую напряженность на q.
Этот способ может показаться излишне сложным — силу, действующую на заряд, можно найти, просто сложив силы, с которыми действуют на него все другие заряды. Действительно, в рамках электростатики эти способы эквивалентны, так как все заряды можно считать все время покоящимися. Однако, как показывает практика, даже в электростатике использование понятия напряженности более удобно. Если же рассматривать движущиеся заряды, то без введения понятия поля обойтись невозможно. Поле — не просто способ описания взаимодействия, а физическая реальность. В частности, поле обладает энергией и импульсом, которые можно измерить.
В заключение необходимо отметить, что электрическое поле может создаваться не только неподвижными зарядами. Такие поля будем в дальнейшем называть сторонними
1.3. Потенциал
На
находящийся в электростатическом поле заряд действует сила. Поэтому при
перемещении заряда из точки 1 в точку 2 силы электростатического поля совершают
работу ![]() ,
зависящую от поля и от величины перемещаемого заряда q. Разность
потенциалов между точками 1 и 2 по определению равна отношению этой работы к
заряду:
,
зависящую от поля и от величины перемещаемого заряда q. Разность
потенциалов между точками 1 и 2 по определению равна отношению этой работы к
заряду:
![]()
Единица измерения потенциала — Вольт.
Так как работа равна интегралу от силы по перемещению
![]()
а электростатическая сила равна произведению заряда на напряженность
![]() ,
,
то получаем связь между потенциалом и напряженностью:
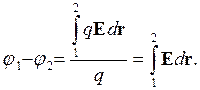
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.