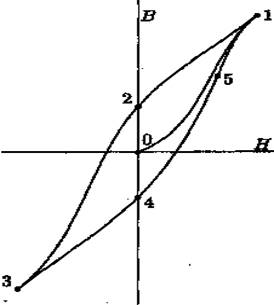
Рис. 39
напряженности магнитного поля). Если затем уменьшать напряженность магнитного поля до отрицательных значений, магнитная индукция в ферромагнетике будет изменяться в соответствии с участком 2-3 графика. При последующем увеличении напряженности магнитного поля магнитная индукция будет изменяться в соответствии с участком графика 3-4-5-1.
Видно, что значение магнитной индукции в ферромагнетике определяется не только действующим в данный момент магнитным полем, но зависит еще от предыдущих состояний намагничивания. Это явление называется магнитным гистерезисом, а петля 1-2-3-4-5-1 на графике — петлей гистерезиса.
Объяснение ферромагнетизма.
В ферромагнетиках имеются межатомные силы, имеющие квантовую природу, которые
ориентируют магнитные моменты атомов параллельно друг другу. Область, в
которой магнитные моменты атомов параллельны, называется доменом; типичный
размер домена порядка 10~4 см. В отсутствии внешнего поля и
остаточного намагничивания все домены ориентированы хаотически. Под действием
внешнего магнитного поля магнитные моменты доменов ориентируются по полю,
сильно увеличивая магнитную индукцию в ферромагнетике. Если поле достаточно
велико, то практически все магнитные домены уже сориентированы по полю, и 
.
При уменьшении либо снятии внешнего поля не все домены разориентируются,
поэтому ферромагнитные материалы могут обладать остаточной намагниченностью.
Именно явлением остаточной намагниченности и объясняется способность многих марок стали намагничиваться в магнитном поле.
4.10. Резюме
Магнитное поле проявляется в том, что на находящуюся в нем частицу с зарядом q и скоростью v действует сила, равная
где В — магнитная индукция. Если имеется еще и электрическое поле с напряженностью Е, то сила, действующая на частицу, равна
Эту силу называют силой Лоренца (часто силой Лоренца называют только силу, обусловленную магнитным полем). Магнитное поле может создаваться электрическим током (более точно, другими движущимися зарядами). Магнитная индукция, создаваемая в произвольной точке пространства элементом провода dl, по которому течет постоянный ток I, равна
гдеr — радиус-вектор, проведенный от элемента dl к этой точке (закон Био-Савара-Лапласа). Чтобы определить магнитную индукцию, создаваемую в произвольной точке всеми токами, необходимо сложить все векторыdB, обусловленные каждым элементом тока, т. е. произвести интегрирование.
Из закона Био-Савара-Лапласа следует, что магнитная индукция, создаваемая бесконечным прямым проводом с током I на расстоянии Л от него, равна по величине
На основе закона Био-Савара-Лапласа можно доказать, что создаваемая токами циркуляция вектора магнитной индукции по произвольному замкнутому контуру g равна произведению μo на сумму токов, пронизывающих любую поверхность, натянутую на этот контур:
Магнитная индукция внутри соленоида, в котором течет ток I, равна
где n — количество витков, приходящихся на единицу длины соленоида.
Так как ток в проводнике обусловлен движением заряженных частиц, а на каждую из них действует сила Лоренца, на элемент dl провода, по которому течет ток I, действует сила, равная
(закон Ампера). На контур с током, находящийся в однородном магнитном поле, действует пара сил, момент этой пары сил равен
или
где Р = ISn — магнитный момент контура, / — ток в контуре, S — площадь контура, n — нормаль к контуру.
В веществе теорему о циркуляции удобнее записывать для вектора напряженности магнитного поля Н:
где в правой части — сумма макротоков. Напряженность магнитного поля равна
где I — магнитный момент единицы объема.
В простейшем случае Н и В пропорциональны друг другу:
(
—
магнитная проницаемость вещества).
Магнитное поле в веществе отличается от магнитного поля в вакууме. Если вещество заполняет всю область пространства, в которой имеется магнитное поле, то магнитная индукция в веществе в р, раз больше, чем в вакууме.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.