Иногда сторонние электрические силы действуют не локально, а сразу во всей цепи. С такой ЭДС на примере ЭДС индукции столкнемся позже.
Всякий реальный источник ЭДС, например, батарейка, может обладать некоторым сопротивлением, его называют внутренним сопротивлением. Во многих случаях можно считать, что реальная ЭДС эквивалентна идеальной ЭДС (т. е. ЭДС без внутреннего сопротивления) и сопротивлению, включенному рядом с ЭДС
последовательно:
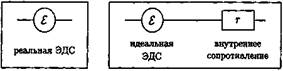
Рис. 20
Итак, закон Ома в интегральной форме более детально формулируется так: произведение силы тока в проводнике на его сопротивление равно напряжению на его концах; напряжение есть сумма разности потенциалов на концах проводника и действующей в проводнике электродвижущей силы:
![]()
Согласно строгому определению напряжения, величина его зависит от того, по какому контуру напряжение определяется. (На практике иногда под напряжением понимают либо разность потенциалов на концах проводника, либо действующую в проводнике ЭДС).
3.6. Правила Кирхгофа
Правила Кирхгофа дают возможность рассчитать токи в разветвленной цепи постоянного тока.
Первое правило Кирхгофа. Сумма токов, сходящихся в узле цепи, равна нулю (см. рис. 21):
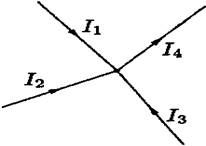
Рис. 21
![]()
(знаки токов, текущих в узел и из него, считаются противоположными).
Доказательство. Заряд, принесенный за время tв узел всеми токами, равен
![]()
Заряд, находящийся в узле, со временем не меняется, поэтому
![]()
следовательно
![]()
т. е. сумма токов равна нулю:
![]()
Второе правило Кирхгофа. Сумма ЭДС в произвольном замкнутом контуре равна сумме произведений силы тока в каждом участке на сопротивление этого участка:
![]()
Доказательство. Рассмотрим произвольный замкнутый контур, например, изображенный на рисунке 22 контур 1-2-3-4-1. Напряжение по этому контуру от точки 1 до точки 1 (через точки 2-3-4) равно сумме напряжений на отдельных участках контура
![]()
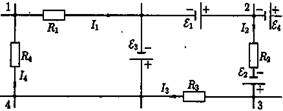
Рис. 22
Но по определению напряжения оно равно разности потенциалов на концах проводника и действующей в проводнике ЭДС:
![]()
Приравнивая, получаем:
![]()
![]()
Согласно закону Ома, напряжение на каждом участке равно произведению тока на сопротивление (U12 =I1R1, U23 = I2R2 и так далее); произведя в последнем выражении эти замены, получаем второе правило Кирхгофа:
![]()
Применение правил Кирхгофа позволяет рассчитать все силы тока в схеме постоянного тока любой сложности. При этом необходимо действовать в определенном порядке:
1. Произвольно расставить стрелки, обозначающие направления всех токов. На каждом неразветвленном участке ставится только одна стрелка.
2. Записать первое правило Кирхгофа для всех узлов схемы, кроме одного.
3. Записать второе правило Кирхгофа для нужного количества замкнутых контуров (полное число уравнений должно быть равным числу всех неизвестных токов). Если выбранное направление обхода контура совпадает с выбранным направлением тока, то соответствующее произведение IR берется со знаком +, если нет — со знаком —. Если по направлению обхода контура приходится проходить сквозь ЭДС от минуса к плюсу, то ЭДС входит со знаком +.
4. Все ЭДС и все сопротивления должны входить в систему уравнений.
Если при решении системы уравнений для каких-то токов получились отрицательные значения, это значит, что ток течет в направлении, обратном выбранному.
3.7. Закон Джоуля-Ленца
При прохождении заряда Q из точки 1 в точку 2 участка цепи над зарядом совершается работа
![]()
Мощность, развиваемая при этом в участке цепи, равна производной от работы по времени:
![]()
Но dQ/dt — это ток в цепи, следовательно мощность равна произведению тока на напряжение:
![]()
Мощность (и, конечно, работа) тока может расходоваться по-разному, например на совершение проводником механической работы (электродвигатели), на химические процессы (гальваника), на излучение электромагнитных волн (антенны), на нагрев участка цепи и т. д. Если вся работа идет только на нагревание проводника, а в проводнике нет ЭДС, то напряжение на концах проводника равно разности потенциалов, тепловая мощность равна
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.