Измерение размеров и контроль качества поверхностей деталей оптико-механическим способом, страница 7

                                                                   U 12 = n1 n 2 = −z1 z 2 ,                                (3)

и внутреннее зацепление (рис. 1, б), при котором зубчатые колеса вращаются в одну сторону и их передаточное отношение берётся со знаком “плюс”:

                                                                      U 12 = n1 n 2 = z1 z 2 .                                 (4)

Передаточное отношение червячной передачи определяется по формуле

                                                                       U 12 = n1 n 2 = z1 k1 ,                                 (5)

где      k₁ - число заходов (витков) червяка.

Для реечной передачи понятия передаточного отношения не существует. Для неё справедлива зависимость между скоростью υ, м с , и угловой скоростью ω, с⁻¹, реечного колеса

                                                                               υ=ωd2000,                                        (6)

где      d - диаметр делительной окружности реечного колеса, мм.

По величине окружной скорости υ зубчатых колёс, определяемой по формуле (6), различают передачи:

-  тихоходные (υ≤ 3 м с),

-  среднескоростные (υ= 3K15 м с), - скоростные (υ=15K40 м с ), - быстроходные (υ> 40 м с).

По форме боковых (рабочих) поверхностей зубьев передачи делятся:

-  на эвольвентные,

-  циклоидальные,

-  с зацеплением М. Л. Новикова (зубья с круговым профилем,

1954 г.).

Преимущественное распространение в приборо- и машиностроении получил эвольвентный профиль зубьев колёс, предложенный академиком Л. Эйлером в 1760 году.

Циклоидальный профиль зубьев, характеризующийся высоким КПД, в настоящее время сохранился лишь в часовых механизмах и некоторых приборах.

Зацепление М. Л. Новикова, обладающее повышенной контактной прочностью (в 1,5...2 раза большей по сравнению с эвольвентным зацеплением) применяется в редукторах общего назначения, в судостроении и др.

По конструктивному исполнению передачи делятся на открытые (не защищенные от влияния внешней среды) и закрытые (изолированные от внешней среды).

Зубчатые передачи по сравнению с другими механическими имеют ряд преимуществ. Они обладают высокой нагрузочной способностью при сравнительно малых габаритах (например, по сравнению с ременными передачами), большой надёжностью и долговечностью (до 40 тысяч часов работы), постоянством передаточного отношения, высоким коэффициентом полезного действия (до 0,97…0,98 для одной пары зубчатых колес при наличии смазки), простотой эксплуатации.

Недостатками этих передач являются повышенные требования к точности изготовления и монтажа, шум при больших окружных скоростях.

2. Геометрия зацепления зубчатых колес

Основная теорема зацепления (теорема Виллиса, см. § 96 [1]) применительно к зубчатой передаче формулируется следующим образом: нормаль n n- , проведенная к боковым профилям зубьев, проходящая через их точку касания, делит межцентровое расстояние a_ω = O O_{1 2} на части, обратно пропорциональные угловым скоростям ω₁ и ω₂ зубчатых колес:

ω1 ω2 =rω2 rω1 , где  r_ω1 и r_ω2 - радиусы так называемых начальных окружностей этих колёс, то есть окружностей, катящихся одна по другой без скольжения (рис. 2).

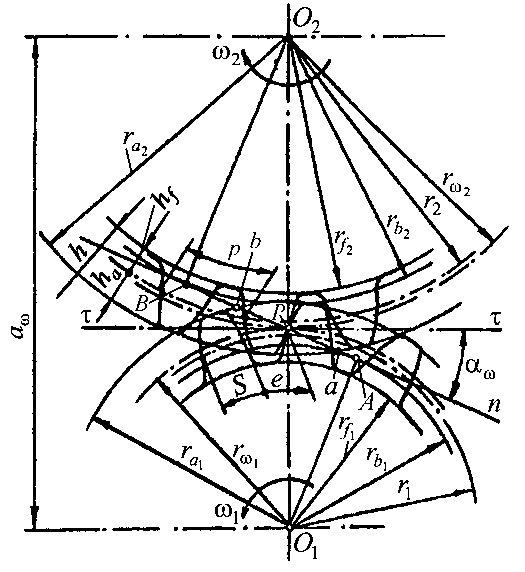
Рис. 2. Геометрия зубчатого зацепления

В соответствии с этой теоремой для обеспечения постоянного передаточного отношения зубчатой передачи (U₁₂ = const ) необходимо, чтобы профили зубьев колёс описывались кривыми, общая нормаль -n n к которым в точке касания независимо от положения этой точки всегда пересекала бы линию центров O O_{1 2} в одной и той же точке Р – полюсе зацепления. Эта общая нормаль -n n называется линией зацепления а угол α_ω между нею и перпендикуляром τ-τ к линии центров O O_{1 2} – углом зацепления.